人教版九年级下册26.1.2 反比例函数的图象与性质 说课课件(共25张PPT)
文档属性
| 名称 | 人教版九年级下册26.1.2 反比例函数的图象与性质 说课课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 907.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览








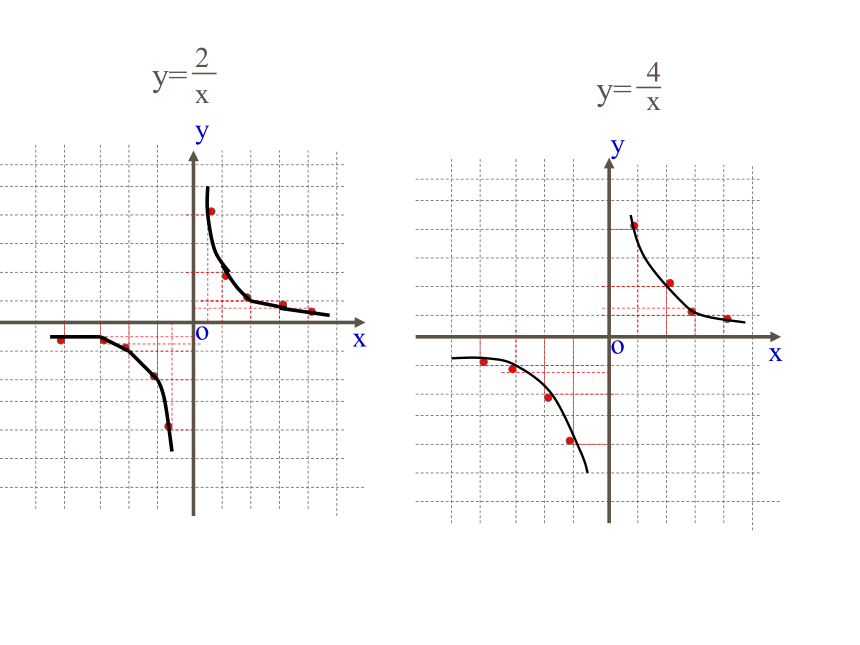
文档简介
(共25张PPT)
(说课课件)
(一)知识目标:
1、使学生会根据函数图象探索反比例函数的主要性质。
2、使学生体会函数的三种表示方法的相互转化,对函数进行认识上的整合。
(二)技能目标:
渗透数形结合的思想和函数思想,培养学生的观察猜想能力、分析归纳能力和有条理的表达能力。
(三)德育目标:
1、使学生体会事物是有规律地变化的观点。
2、培养学生初步的辩证唯物主义“运动变化”的观点和浓厚的学习兴趣。
教学目标
教 学重点
探索反比例函数的主要性质
教学难点:
归纳概括反比例函数图象的
主要特征
引导发现法
分组讨论法
媒体演示法
t=- 说一说时间随速度增加而怎样变化
v
110
p=- (F是常数)说一说地面压强随面积的减少而怎样变化
F
S
画出面积是20平方厘米的长方形
ab=20cm2
(说一说长方形的宽随长的增加而怎样变化。)
o
y
x
o
y
x
y=-
x
2
y=-
x
4
细观察 找规律:
1、图象分别位于哪几个象限内?
2、在每一象限内,y随x增大而怎样变化?
3、反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?
(借助解析式,因为k 永不为0,所以x、y都不为0,所以图象与x轴、y轴有交点吗?)
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
?
O
1、当k>0时,图象的两个分支分别在第一、三象限内,在每一象限内,y随x的增大而减小;
2、当k<0时,图象的两个分支分别在第二、四象限内,在每一象限内,y随x的增大而增大。
-2
-3
3
2
A/
A
x
y
y=-
x
6
(1)写出A、A/两点的坐标,
(2)分别过点A、和A/作x轴的垂线,垂足分别是B和B/,则下列关系正确吗?为什么?
(A)OA=OA/ (B)∠AOB= ∠A /OB / (C)点A、O、A /在同一条直线上。
O
B
B/
反比例函数是轴对称图形它的对称轴是:坐标轴的两条角平分线。
反比例函数也是中心对称图形它的对称中心是:坐标轴的原点。
y=-的图象上任取A、B两点,过这两点分别作x轴、y轴的垂线,与坐标轴围成的矩形面积为S,观察S的变化情况,并找出其中规律。
k
x
o
x
y
A(3,2)
B(-3,-2)
C
D
E
F
y=-
x
6
SACOD=6
SBFOE=6
巩固练习:
2、下列函数中,其图象位于第一三象限的有哪几个?在其图象所在象限内,y随x增大而增大的有哪几个?
(1)y=1/2x (2)y=0.3/x (3)y=10/x (4)y=7/100x
1、反比例函数y=4/x的图象上三点A(-2,y 1),B(1,y2),C(3,y3)
比较y 1、 y2、 y3的大小。
3、在函数y=-6/x的图象上取三点,由这三点分别向x、y作垂线,让矩形AA1OA2 BB1OB2 CC1 OC2面积分别为SA、SB、SC,则SA、 SB、 SC 大小关系。
课堂小结:
总结本堂课所学知识你有那些体会和收获
作 业
教材143页习题5.3第1、2、题
思考题:双曲线越来越接近坐标轴,但为什么永不能与坐标轴相交?
板书设计:
1、性质:k 0时,双曲线的两个分支在一三象限y随x增大而减小;
k 0时,双曲线的两个分支在二四象限y随x增大而增大。
反比例函数图象的性质
2、反比例函数是中心对称图形也是轴对称图形。
总之,我对本节课教学设计的指导思想是:以实现教学目标为前提;以现代教育理论为基础;以基本的教学原则为指导,以现代信息技术为手段来实现教学最优化,从而提高教与学的质量。
(说课课件)
(一)知识目标:
1、使学生会根据函数图象探索反比例函数的主要性质。
2、使学生体会函数的三种表示方法的相互转化,对函数进行认识上的整合。
(二)技能目标:
渗透数形结合的思想和函数思想,培养学生的观察猜想能力、分析归纳能力和有条理的表达能力。
(三)德育目标:
1、使学生体会事物是有规律地变化的观点。
2、培养学生初步的辩证唯物主义“运动变化”的观点和浓厚的学习兴趣。
教学目标
教 学重点
探索反比例函数的主要性质
教学难点:
归纳概括反比例函数图象的
主要特征
引导发现法
分组讨论法
媒体演示法
t=- 说一说时间随速度增加而怎样变化
v
110
p=- (F是常数)说一说地面压强随面积的减少而怎样变化
F
S
画出面积是20平方厘米的长方形
ab=20cm2
(说一说长方形的宽随长的增加而怎样变化。)
o
y
x
o
y
x
y=-
x
2
y=-
x
4
细观察 找规律:
1、图象分别位于哪几个象限内?
2、在每一象限内,y随x增大而怎样变化?
3、反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?
(借助解析式,因为k 永不为0,所以x、y都不为0,所以图象与x轴、y轴有交点吗?)
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
?
O
1、当k>0时,图象的两个分支分别在第一、三象限内,在每一象限内,y随x的增大而减小;
2、当k<0时,图象的两个分支分别在第二、四象限内,在每一象限内,y随x的增大而增大。
-2
-3
3
2
A/
A
x
y
y=-
x
6
(1)写出A、A/两点的坐标,
(2)分别过点A、和A/作x轴的垂线,垂足分别是B和B/,则下列关系正确吗?为什么?
(A)OA=OA/ (B)∠AOB= ∠A /OB / (C)点A、O、A /在同一条直线上。
O
B
B/
反比例函数是轴对称图形它的对称轴是:坐标轴的两条角平分线。
反比例函数也是中心对称图形它的对称中心是:坐标轴的原点。
y=-的图象上任取A、B两点,过这两点分别作x轴、y轴的垂线,与坐标轴围成的矩形面积为S,观察S的变化情况,并找出其中规律。
k
x
o
x
y
A(3,2)
B(-3,-2)
C
D
E
F
y=-
x
6
SACOD=6
SBFOE=6
巩固练习:
2、下列函数中,其图象位于第一三象限的有哪几个?在其图象所在象限内,y随x增大而增大的有哪几个?
(1)y=1/2x (2)y=0.3/x (3)y=10/x (4)y=7/100x
1、反比例函数y=4/x的图象上三点A(-2,y 1),B(1,y2),C(3,y3)
比较y 1、 y2、 y3的大小。
3、在函数y=-6/x的图象上取三点,由这三点分别向x、y作垂线,让矩形AA1OA2 BB1OB2 CC1 OC2面积分别为SA、SB、SC,则SA、 SB、 SC 大小关系。
课堂小结:
总结本堂课所学知识你有那些体会和收获
作 业
教材143页习题5.3第1、2、题
思考题:双曲线越来越接近坐标轴,但为什么永不能与坐标轴相交?
板书设计:
1、性质:k 0时,双曲线的两个分支在一三象限y随x增大而减小;
k 0时,双曲线的两个分支在二四象限y随x增大而增大。
反比例函数图象的性质
2、反比例函数是中心对称图形也是轴对称图形。
总之,我对本节课教学设计的指导思想是:以实现教学目标为前提;以现代教育理论为基础;以基本的教学原则为指导,以现代信息技术为手段来实现教学最优化,从而提高教与学的质量。
