人教版八年级上数学第十四章《14.1---14.2乘法公式》测试卷(含解析)
文档属性
| 名称 | 人教版八年级上数学第十四章《14.1---14.2乘法公式》测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 77.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 18:39:39 | ||
图片预览




文档简介
八年级上数学第十四章《14.1---14.2乘法公式》检测题
测试时间:90分钟 时间满分:120分
选择题(每小题3分,共30分)
1.(2022秋 肇源县期中)下列运算正确的是( )
A.aa2=a2 B.(ab)3=ab3 C.(a2)3=a6 D.a10÷a2=a5
2.(2022秋 丹江口市期中)若(x+3)(x+m)展开合并后的一次项系数为﹣1,则m的值为( )
A.﹣4 B.4 C.﹣2 D.2
3.(2022秋 泉州期中)已知a2﹣3a+1=0,则(a+1)(a﹣4)的值为( )
A.不确定 B.5 C.﹣3 D.﹣5
4.(2022秋 南召县期中)设A=(x﹣1)(x﹣5),B=(x﹣4)(x﹣2),则A,B的大小关系为( )
A.A>B B.A<B C.A=B D.无法确定
5.(2022秋 衡南县期中)下列能使用平方差公式的是( )
A.(x+3)(x+x) B.(﹣x+y)(x﹣y)
C.(m+n)(m﹣n) D.(3m+n)(3m﹣n)
6.(2022秋 崇川区期中)已知:a+b=3,a﹣b=1,则a2﹣b2等于( )
A.1 B.2 C.3 D.4
7.(2022秋 闵行区校级期中)若多项式4x2+mxy+9y2是完全平方式,则m的值为( )
A.6或﹣6 B.12或﹣12 C.12 D.﹣12
8.(2022秋 晋江市期中)计算:9992﹣998×1002=( )
A.﹣2000 B.﹣1995 C.1995 D.2000
9.(2022秋 渝北区校级期中)已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A. B. C.﹣3 D.3
10.(2021秋 沙坪坝区校级期末)如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中小正方形的面积为4,每个小长方形的面积为15,若用x,y分别表示小长方形的长与宽(其中xy),现给出以下关系式:①x﹣y=3;②x+y=8;③x2﹣y2=16;④x2+y2=34.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
填空题(每小题3分,共24分)
12.(2022秋 晋江市期中)计算:(a6﹣2a3)÷a3= .
13.(2022秋 海安市期中)已知10a=20,100b=50,则a+2b+3= .
14.(2022春 吴江区校级期中)若x2+2x=﹣1,则代数式6+x(x+2)的值为 .
15.(2022春 新邵县期末)数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“﹣2x2(3x﹣■+1)=﹣6x3+4x2y﹣2x2”那么“■”中的一项是 .
16.(2022秋 锡山区校级月考)一块长方形地长18米,如果把它的长增加到22米,宽减少3米,面积的大小正好不变,这块长方形地的面积是 平方米.
17.(2022秋 安溪县期中)若a﹣b=3,ab=﹣4,则(a+2)(b﹣2)的值为 .
18.(2022秋 思明区校级期中)若a+b=2,则多项式a2+4b﹣b2的值是 .
19.(2021秋 东兴区校级期中)已知a+b=8,ab=c2+16,则a+2b+3c= .
三、解答题(共66分)
19.(每小题4分,共16分)计算:
(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3. (2)﹣(a2b)3+2a2b (﹣3a2b)2;
(3)4x(1﹣3x)+2(6x2+3x﹣1); (5)(a+2b)(a﹣2b)+(3a﹣2b)2.
19.(5分)先化简再求值:[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y,其中x=1,y=﹣1.
20.(6分)(2022秋 南安市期中)已知(x+a)(x2﹣bx﹣1)展开后不含x的二次项,且含x的一次项系数是﹣4,求a2+b2的值.
21.(6分)(2022春 滕州市校级月考)如图,在长为3a+2,宽为2b﹣1的长方形铁片上,挖去长为2a+4,宽为b的小长方形铁片.
(1)求剩余部分面积.
(2)求出当a=3,b=2时的面积.
22.(7分)(2022秋 永春县校级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂ab和cb,当a>c时,则有ab>cb,根据上述材料,回答下列问题.
(1)比较大小:520 420(填写>、<或=).
(2)比较233与322的大小(写出具体过程).
(3)已知2a=3,8b=6,求(28+2b)3的值.
23.(8分)(2022春 东台市期中)小刚同学计算一道整式乘法:(3x+a)(2x﹣3),由于他抄错了多项式中a前面的符号,把“+”写成“﹣”,得到的结果为6x2+bx+12
(1)求a,b的值;
(2)计算这道整式乘法的正确结果.
24.(8分)(2022秋 如皋市期中)在学方差公式”时,张老师出了一道题:计算9×11×101.嘉嘉发现把9写成(10﹣1),把11写成(10+1)后可以连续运用平方差公式进行计算.
请根据上述思路,计算:
(1)9×11×101;
(2).
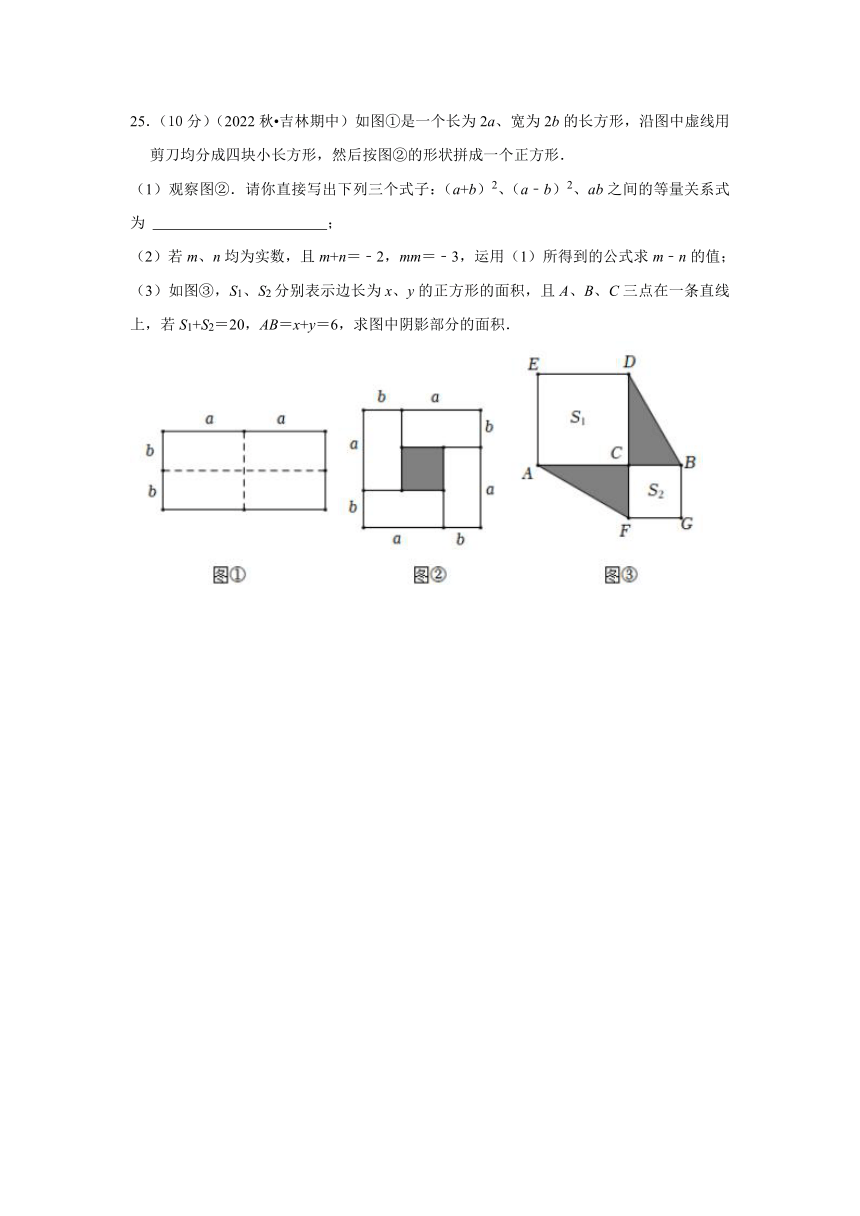
25.(10分)(2022秋 吉林期中)如图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)观察图②.请你直接写出下列三个式子:(a+b)2、(a﹣b)2、ab之间的等量关系式为 ;
(2)若m、n均为实数,且m+n=﹣2,mm=﹣3,运用(1)所得到的公式求m﹣n的值;
(3)如图③,S1、S2分别表示边长为x、y的正方形的面积,且A、B、C三点在一条直线上,若S1+S2=20,AB=x+y=6,求图中阴影部分的面积.
八年级上数学第十四章《14.1---14.2乘法公式》检测题
(解析版)
测试时间:90分钟 时间满分:120分
选择题(每小题3分,共30分)
1.(2022秋 肇源县期中)下列运算正确的是( )
A.aa2=a2 B.(ab)3=ab3 C.(a2)3=a6 D.a10÷a2=a5
【分析】根据同底数幂的乘除运算、积的乘方以及幂的乘方运算即可求出答案.
【解答】解:A、原式=a3,故A不符合题意.
B、原式=a3b3,故B不符合题意.
C、原式=a6,故C符合题意.
D、原式=a8,故D不符合题意.
故选:C.
【点评】本题考查同底数幂的乘除运算、积的乘方以及幂的乘方运算,本题属于基础题型.
2.(2022秋 丹江口市期中)若(x+3)(x+m)展开合并后的一次项系数为﹣1,则m的值为( )
A.﹣4 B.4 C.﹣2 D.2
【分析】利用多项式乘多项式法则计算,然后根据合并后的一次项系数为﹣1,得出3+m=﹣1,然后进行计算,即可得出答案.
【解答】解:(x+3)(x+m)=x2+(3+m)x+3m,
∵(x+3)(x+m)展开合并后的一次项系数为﹣1,
∴3+m=﹣1,
∴m=﹣4.
故选:A.
【点评】此题考查了多项式乘多项式的法则,熟练掌握法则是解本题的关键.
3.(2022秋 泉州期中)已知a2﹣3a+1=0,则(a+1)(a﹣4)的值为( )
A.不确定 B.5 C.﹣3 D.﹣5
【分析】由题意可得:a2﹣3a=﹣1,再利用多项式乘多项式的法则对所求的式子进行运算,再整体代入即可.
【解答】解:∵a2﹣3a+1=0,
∴a2﹣3a=﹣1,
∴(a+1)(a﹣4)
=a2﹣4a+a﹣4
=a2﹣3a﹣4
=﹣1﹣4
=﹣5,
故选:D.
【点评】本题主要考查多项式乘多项式,整体思想,解答的关键是对相应的运算法则的掌握.
4.(2022秋 南召县期中)设A=(x﹣1)(x﹣5),B=(x﹣4)(x﹣2),则A,B的大小关系为( )
A.A>B B.A<B C.A=B D.无法确定
【分析】根据多项式乘多项式的法则先进行计算,再利用作差法比较A、B的大小,即可得出答案.
【解答】解:∵A=(x﹣1)(x﹣5),B=(x﹣2)(x﹣4),
∴A﹣B=(x﹣1)(x﹣5)﹣(x﹣2)(x﹣4)=(x2﹣6x+5)﹣(x2﹣6x+8)=﹣3<0,
∴A<B.
故选:B.
【点评】本题主要考查了多项式乘多项式,运用作差法比较大小是解题的关键.
5.(2022秋 衡南县期中)下列能使用平方差公式的是( )
A.(x+3)(x+x) B.(﹣x+y)(x﹣y)
C.(m+n)(m﹣n) D.(3m+n)(3m﹣n)
【分析】利用平方差公式的特点,完全平方公式的特点对每个选项进行分析,即可得出答案.
【解答】解:(x+3)(x+x),不符合平方差公式的特点,
∴选项A不符合题意;
∵(﹣x+y)(x﹣y)=﹣(x﹣y)2,
∴选项B不符合题意;
∵(m+n)(m﹣n)=﹣(m+n)2,不符合平方差公式的特点,
∴选项C不符合题意;
∵(3m+n)(3m﹣n),符合平方差公式的特点,
∴选项D符合题意;
故选:D.
【点评】本题考查了平方差公式,完全平方公式,掌握平方差公式的特点,完全平方公式的特点是解决问题的关键.
6.(2022秋 崇川区期中)已知:a+b=3,a﹣b=1,则a2﹣b2等于( )
A.1 B.2 C.3 D.4
【分析】根据平方差公式即可得出答案.
【解答】解:∵a+b=3,a﹣b=1,
∴原式=(a+b)(a﹣b)
=3×1
=3.
故选:C.
【点评】本题考查了平方差公式,掌握(a+b)(a﹣b)=a2﹣b2是解题的关键.
7.(2022秋 闵行区校级期中)若多项式4x2+mxy+9y2是完全平方式,则m的值为( )
A.6或﹣6 B.12或﹣12 C.12 D.﹣12
【分析】利用完全平方公式的结构特征判断即可得到m的值.
【解答】解:∵4x2+mxy+9y2是完全平方式,
∴(2x)2±2 2x 3y+(3y)2
∴mxy=±12xy,
m=±12,
故选:B.
【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
8.(2022秋 晋江市期中)计算:9992﹣998×1002=( )
A.﹣2000 B.﹣1995 C.1995 D.2000
【分析】将999转化为(1000﹣1),利用完全平方公式计算;将998写成(1000﹣2),将1002写成(1000+2),即可按照平方差公式进行计算.
【解答】解:9992﹣998×1002
=(1000﹣1)2﹣(1000﹣2)(1000+2)
=10002﹣2×1000×1+1﹣10002+4
=﹣2000+5
=﹣1995.
故选:B.
【点评】本题考查了平方差公式和完全平方公式在简便计算中的应用,熟练掌握平方差公式和完全平方公式是解题的关键.
9.(2022秋 渝北区校级期中)已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A. B. C.﹣3 D.3
【分析】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解答】解:(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b,
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴a﹣3b=0,2a﹣b=﹣5,
解得:a=﹣3,b=﹣1,
∴ab.
故选:A.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
10.(2021秋 沙坪坝区校级期末)如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中小正方形的面积为4,每个小长方形的面积为15,若用x,y分别表示小长方形的长与宽(其中xy),现给出以下关系式:①x﹣y=3;②x+y=8;③x2﹣y2=16;④x2+y2=34.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据几何意义可得,(x﹣y)2=4,xy=15,再根据整式间关系可判断每个结论的正误.
【解答】解:由题意得,(x﹣y)2=4,xy=15,
∴x﹣y2;
x+y8;
x2﹣y2=(x+y) (x﹣y)=2×8=16;
x2+y2=(x﹣y)2+2xy=4+2×15=4+30=34,
故②③④正确,
故选:C.
【点评】本题考查对完全平方公式几何意义的理解,关键是能理解完全平方公式的几何意义,去推导整式间的正确关系.
填空题(每小题3分,共24分)
12.(2022秋 晋江市期中)计算:(a6﹣2a3)÷a3= .
【分析】根据多项式除以单项式的运算法则计算即可.
【解答】解:(a6﹣2a3)÷a3
=a6÷a3﹣2a3÷a3
=a3﹣2.
故答案为:a3﹣2.
【点评】本题考查了整式的乘法,掌握多项式除以单项式的运算法则是解答本题的关键.
13.(2022秋 海安市期中)已知10a=20,100b=50,则a+2b+3= .
【分析】根据100b=50求出102b=50,根据同底数幂的乘法法则得出10a+2b=1000=103,求出a+2b=3,再求出答案即可.
【解答】解:∵100b=50,
∴(102)b=50,
∴102b=50,
∵10a=20,
∴10a×102b=20×50=1000=103,
∴10a+2b=103,
∴a+2b=3,
∴a+2b+3=3+3=6,
故答案为:6.
【点评】本题考查了幂的乘方与积的乘方和同底数幂的乘法,能求出10a+2b=103是解此题的关键.
14.(2022春 吴江区校级期中)若x2+2x=﹣1,则代数式6+x(x+2)的值为 .
【分析】利用单项式乘多项式的法则对所求的式子进行运算,再整体代入已知的条件运算即可.
【解答】解:当x2+2x=﹣1时,
6+x(x+2)
=6+(x2+2x)
=6+(﹣1)
=5.
故答案为:5.
【点评】本题主要考查单项式乘多项式,解答的关键是对相应的运算法则的掌握.
15.(2022春 新邵县期末)数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“﹣2x2(3x﹣■+1)=﹣6x3+4x2y﹣2x2”那么“■”中的一项是 .
【分析】利用多项式除以单项式法则计算(﹣6x3+4x2y﹣2x2)÷(﹣2x2)即可得出“■”中的项,然后利用单项式乘多项式的法则进行计算验证即可.
【解答】解:∵(﹣6x3+4x2y﹣2x2)÷(﹣2x2)
=﹣6x3÷(﹣2x2)+4x2y÷(﹣2x2)﹣2x2÷(﹣2x2)
=3x﹣2y+1,
即﹣2x2(3x﹣2y+1)=﹣6x3+4x2y﹣2x2,
∴“■”中的一项是2y.
故答案为:2y.
【点评】此题考查了单项式乘多项式,熟练掌握运算法则是解本题的关键.单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
16.(2022秋 锡山区校级月考)一块长方形地长18米,如果把它的长增加到22米,宽减少3米,面积的大小正好不变,这块长方形地的面积是 平方米.
【分析】根据题意知:原来长方形的长×原长方形的宽=增加后的长×(原来的宽﹣3),据此可列出方程求出长方形的宽是多少,再根据长方形的面积公式S=ab可求出长方形的面积.
【解答】解:设原长方形的宽为x,根据题意得:
18x=22×(x﹣3),
18x=22x﹣66,
22x﹣18x=66,
4x=66,
x=16.5,
18×16.5=297(平方米),
答:这块长方形地的面积是297平方米.
故答案为:297.
【点评】此题考查了多项式乘多项式,重点是列出方程求出原来长方形的宽,再根据长方形的面积公式进行解答.
17.(2022秋 安溪县期中)若a﹣b=3,ab=﹣4,则(a+2)(b﹣2)的值为 .
【分析】先去括号,再合并同类项,最后整体代入计算即可.
【解答】解:∵(a+2)(b﹣2)
=ab﹣2(a﹣b)﹣4,
a﹣b=3,ab=﹣4,
∴原式=﹣4﹣6﹣4
=﹣14,
故答案为:﹣14.
【点评】本题主要考查了多项式乘多项式,掌握多项式与多项式相乘的法则是解题关键.
18.(2022秋 思明区校级期中)若a+b=2,则多项式a2+4b﹣b2的值是 .
【分析】把a2+4b﹣b2化为(a+b)(a﹣b)+4b的形式,再整体代入计算.
【解答】解:∵a+b=2,
∴a2+4b﹣b2
=a2﹣b2+4b
=(a+b)(a﹣b)+4b
=2(a+b)
=4,
故答案为:4.
【点评】本题考查平方差公式,掌握平方差公式的应用是解题关键.
19.(2021秋 东兴区校级期中)已知a+b=8,ab=c2+16,则a+2b+3c= .
【分析】根据已知a+b=8将等号两边平方,可得到a2+2ab+b2=64=4×16.c2+16的16看作ab﹣c2,代入移项、运用完全平方差公式转化为
(a﹣b)2+4c2=0.再根据非负数的性质与已知a+b=8,可求出a、b、c的值.代入即求得计算结果.
【解答】解:∵a+b=8
∴a2+2ab+b2=64
∵ab=c2+16
∴16=ab﹣c2
∴a2+2ab+b2=64=4×16=4(ab﹣c2)=4ab﹣4c2,即(a﹣b)2+4c2=0
∴a=b,c=0
又∵a+b=8
∴a=b=4
∴a+2b+3c=4+2×4+3×0=12
故答案为12
【点评】本题考查完全平方式与非负数的性质.同学们特别要注意我们一般是将式子用数值来代入,但对于本题是将数值16用ab﹣c2来代入.
三、解答题(共66分)
19.(每小题4分,共16分)计算:
(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3. (2)﹣(a2b)3+2a2b (﹣3a2b)2;
(3)4x(1﹣3x)+2(6x2+3x﹣1); (5)(a+2b)(a﹣2b)+(3a﹣2b)2.
【分析】(1)先算幂的乘方,再算同底数幂的乘法,最后合并同类项即可.
(2)先算乘方,后算乘法,最后算加法;
(3)根据单项式乘多项式的法则展开,合并同类项即可;
(4)根据平方差公式、完全平方公式进行化简即可求出答案.
【解答】解:(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3
=﹣(﹣x6) x4﹣x (﹣x9)
=x10+x10
=2x10.
(2)﹣(a2b)3+2a2b (﹣3a2b)2;
=﹣a6b3+2a2b 9a4b2
=﹣a6b3+18a6b3
=17a6b3;
(3)原式=4x﹣12x2+12x2+6x﹣2
=10x﹣2;
(4)原式=a2﹣4b2+9a2﹣12ab+4b2
=10a2﹣12ab.
【点评】本题主要考查整式的乘法及乘法公式,解答的关键是对相应的运算法则的掌握.
19.(5分)先化简再求值:[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y,其中x=1,y=﹣1.
【分析】原式中括号中利用平方差公式,以及完全平方公式化简,去括号合并后,利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】原式=(x2﹣4y2﹣x2﹣8xy﹣16y2)÷4y
=(﹣20y2﹣8xy)÷4y
=﹣5y﹣2x,
当x=1,y=﹣1时,原式=5﹣2=3.
【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.
20.(6分)(2022秋 南安市期中)已知(x+a)(x2﹣bx﹣1)展开后不含x的二次项,且含x的一次项系数是﹣4,求a2+b2的值.
【分析】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解答】解:(x+a)(x2﹣bx﹣1)
=x3﹣bx2﹣x+ax2﹣abx﹣a
=x3+(﹣b+a)x2+(﹣1﹣ab)x﹣a,
∵展开后不含x的二次项,且含x的一次项系数是﹣4,
∴﹣b+a=0,﹣1﹣ab=﹣4,
得:a=b,ab=3,
∴a2+b2
=(a﹣b)2+2ab
=02+2×3
=0+6
=6.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
21.(6分)(2022春 滕州市校级月考)如图,在长为3a+2,宽为2b﹣1的长方形铁片上,挖去长为2a+4,宽为b的小长方形铁片.
(1)求剩余部分面积.
(2)求出当a=3,b=2时的面积.
【分析】(1)阴影部分面积=原长方形的面积﹣挖去的长方形的面积,据此即可求解;
(2)把相应的值代入(1)运算即可.
【解答】解:(1)由题意得:
S阴影=S原长方形﹣S挖去的长方形
=(3a+2)(2b﹣1)﹣(2a+4)b
=6ab﹣3a+4b﹣2﹣2ab﹣4b
=4ab﹣3a﹣2;
(2)当a=3,b=2时,
原式=4×3×2﹣3×3﹣2
=24﹣9﹣2
=13.
【点评】本题主要考查多项式乘多项式,单项式乘多项式,解答的关键是对相应的运算法则的掌握与运用.
22.(7分)(2022春 兰溪市期中)已知:x+y=6,xy=3.求下列各式的值:
(1)x2+4xy+y2
(2)x4+y4
【分析】(1)利用完全平方公式变形可得答案;
(2)首先求出x2+y2=30,再根据完全平方公式变形可得答案.
【解答】解:(1)∵x+y=6,xy=3,
∴x2+4xy+y2
=x2+2xy+y2+2xy
=(x+y)2+2xy
=36+6
=42;
(2)∵x+y=6,xy=3,
∴x2+y2=(x+y)2﹣2xy=36﹣6=30,
∴x4+y4=(x2+y2)2﹣2x2y2
=900﹣2×9
=900﹣18
=882.
【点评】本题考查乘法公式的运用,熟练掌握完全平方公式是解题关键.
23.(8分)(2022春 东台市期中)小刚同学计算一道整式乘法:(3x+a)(2x﹣3),由于他抄错了多项式中a前面的符号,把“+”写成“﹣”,得到的结果为6x2+bx+12
(1)求a,b的值;
(2)计算这道整式乘法的正确结果.
【分析】(1)由题意得(3x﹣a)(2x﹣3)=6x2+bx+12,进而得出6x2﹣(2a+9)x+3a=6x2+bx+12,根据对应系数相等即可求出a,b的值;
(2)把a=4代入(3x+a)(2x﹣3),依据多项式乘多项式的法则进行计算,即可得出正确结果.
【解答】解:(1)由题意得:(3x﹣a)(2x﹣3)=6x2+bx+12,
∴6x2﹣(2a+9)x+3a=6x2+bx+12,
∴﹣(2a+9)=b,3a=12,
∴a=4,b=﹣17;
(2)(3x+4)(2x﹣3)
=6x2﹣9x+8x﹣12
=6x2﹣x﹣12.
【点评】本题考查了多项式乘多项式,掌握多项式乘多项式的法则是解决问题的关键.
24.(8分)(2022秋 如皋市期中)在学方差公式”时,张老师出了一道题:计算9×11×101.嘉嘉发现把9写成(10﹣1),把11写成(10+1)后可以连续运用平方差公式进行计算.
请根据上述思路,计算:
(1)9×11×101;
(2).
【分析】(1)将原式化为(10﹣1)×(10+1)×(100+1),连续利用平方差公式进行计算即可;
(2)将改写成(1)后,连续利用平方差公式进行计算即可.
【解答】解:(1)原式=(10﹣1)×(10+1)×(100+1)
=(102﹣1)×(100+1)
=(100﹣1)×(100+1)
=1002﹣1
=10000﹣1
=9999;
(2)原式=(1)×(1)×(1)×(1)×(1)
=(1)×(1)×(1)×(1)
=(1)×(1)×(1)
=(1)×(1)
=1
=1.
【点评】本题考查平方差公式,掌握平方差公式的结构特征是正确应用的前提.
25.(10分)(2022秋 吉林期中)如图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)观察图②.请你直接写出下列三个式子:(a+b)2、(a﹣b)2、ab之间的等量关系式为 ;
(2)若m、n均为实数,且m+n=﹣2,mm=﹣3,运用(1)所得到的公式求m﹣n的值;
(3)如图③,S1、S2分别表示边长为x、y的正方形的面积,且A、B、C三点在一条直线上,若S1+S2=20,AB=x+y=6,求图中阴影部分的面积.
【分析】(1)由图象中小正方形面积=大正方形面积﹣长方形面积求解.
(2)根据(m+n)2﹣(m﹣n)2=4mn求解.
(3)由xx20,x+y=6,S阴影=S△ACF+S△BCD求解.
【解答】解:(1)由图象可得:(a+b)2﹣(a﹣b)2=4ab.
故答案为:(a+b)2﹣(a﹣b)2=4ab.
(2)∵(m+n)2﹣(m﹣n)2=4mn,
∴(m﹣n)2=(m+n)2﹣4mn,
∵m+n=﹣2,mn=﹣3,
∴(m﹣n)2=(﹣2)2﹣4×(﹣3)=16.
(3)∵S1+S2=20,
∴xx20,
∴S阴影=S△ACF+S△BCDx1 x2x1 x2=x1 x2[(x1+x2)2﹣(xx)](62﹣20)=8.
【点评】本题考查完全平方式的应用,解题关键是熟练掌握完全平放式.
测试时间:90分钟 时间满分:120分
选择题(每小题3分,共30分)
1.(2022秋 肇源县期中)下列运算正确的是( )
A.aa2=a2 B.(ab)3=ab3 C.(a2)3=a6 D.a10÷a2=a5
2.(2022秋 丹江口市期中)若(x+3)(x+m)展开合并后的一次项系数为﹣1,则m的值为( )
A.﹣4 B.4 C.﹣2 D.2
3.(2022秋 泉州期中)已知a2﹣3a+1=0,则(a+1)(a﹣4)的值为( )
A.不确定 B.5 C.﹣3 D.﹣5
4.(2022秋 南召县期中)设A=(x﹣1)(x﹣5),B=(x﹣4)(x﹣2),则A,B的大小关系为( )
A.A>B B.A<B C.A=B D.无法确定
5.(2022秋 衡南县期中)下列能使用平方差公式的是( )
A.(x+3)(x+x) B.(﹣x+y)(x﹣y)
C.(m+n)(m﹣n) D.(3m+n)(3m﹣n)
6.(2022秋 崇川区期中)已知:a+b=3,a﹣b=1,则a2﹣b2等于( )
A.1 B.2 C.3 D.4
7.(2022秋 闵行区校级期中)若多项式4x2+mxy+9y2是完全平方式,则m的值为( )
A.6或﹣6 B.12或﹣12 C.12 D.﹣12
8.(2022秋 晋江市期中)计算:9992﹣998×1002=( )
A.﹣2000 B.﹣1995 C.1995 D.2000
9.(2022秋 渝北区校级期中)已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A. B. C.﹣3 D.3
10.(2021秋 沙坪坝区校级期末)如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中小正方形的面积为4,每个小长方形的面积为15,若用x,y分别表示小长方形的长与宽(其中xy),现给出以下关系式:①x﹣y=3;②x+y=8;③x2﹣y2=16;④x2+y2=34.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
填空题(每小题3分,共24分)
12.(2022秋 晋江市期中)计算:(a6﹣2a3)÷a3= .
13.(2022秋 海安市期中)已知10a=20,100b=50,则a+2b+3= .
14.(2022春 吴江区校级期中)若x2+2x=﹣1,则代数式6+x(x+2)的值为 .
15.(2022春 新邵县期末)数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“﹣2x2(3x﹣■+1)=﹣6x3+4x2y﹣2x2”那么“■”中的一项是 .
16.(2022秋 锡山区校级月考)一块长方形地长18米,如果把它的长增加到22米,宽减少3米,面积的大小正好不变,这块长方形地的面积是 平方米.
17.(2022秋 安溪县期中)若a﹣b=3,ab=﹣4,则(a+2)(b﹣2)的值为 .
18.(2022秋 思明区校级期中)若a+b=2,则多项式a2+4b﹣b2的值是 .
19.(2021秋 东兴区校级期中)已知a+b=8,ab=c2+16,则a+2b+3c= .
三、解答题(共66分)
19.(每小题4分,共16分)计算:
(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3. (2)﹣(a2b)3+2a2b (﹣3a2b)2;
(3)4x(1﹣3x)+2(6x2+3x﹣1); (5)(a+2b)(a﹣2b)+(3a﹣2b)2.
19.(5分)先化简再求值:[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y,其中x=1,y=﹣1.
20.(6分)(2022秋 南安市期中)已知(x+a)(x2﹣bx﹣1)展开后不含x的二次项,且含x的一次项系数是﹣4,求a2+b2的值.
21.(6分)(2022春 滕州市校级月考)如图,在长为3a+2,宽为2b﹣1的长方形铁片上,挖去长为2a+4,宽为b的小长方形铁片.
(1)求剩余部分面积.
(2)求出当a=3,b=2时的面积.
22.(7分)(2022秋 永春县校级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂ab和cb,当a>c时,则有ab>cb,根据上述材料,回答下列问题.
(1)比较大小:520 420(填写>、<或=).
(2)比较233与322的大小(写出具体过程).
(3)已知2a=3,8b=6,求(28+2b)3的值.
23.(8分)(2022春 东台市期中)小刚同学计算一道整式乘法:(3x+a)(2x﹣3),由于他抄错了多项式中a前面的符号,把“+”写成“﹣”,得到的结果为6x2+bx+12
(1)求a,b的值;
(2)计算这道整式乘法的正确结果.
24.(8分)(2022秋 如皋市期中)在学方差公式”时,张老师出了一道题:计算9×11×101.嘉嘉发现把9写成(10﹣1),把11写成(10+1)后可以连续运用平方差公式进行计算.
请根据上述思路,计算:
(1)9×11×101;
(2).
25.(10分)(2022秋 吉林期中)如图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)观察图②.请你直接写出下列三个式子:(a+b)2、(a﹣b)2、ab之间的等量关系式为 ;
(2)若m、n均为实数,且m+n=﹣2,mm=﹣3,运用(1)所得到的公式求m﹣n的值;
(3)如图③,S1、S2分别表示边长为x、y的正方形的面积,且A、B、C三点在一条直线上,若S1+S2=20,AB=x+y=6,求图中阴影部分的面积.
八年级上数学第十四章《14.1---14.2乘法公式》检测题
(解析版)
测试时间:90分钟 时间满分:120分
选择题(每小题3分,共30分)
1.(2022秋 肇源县期中)下列运算正确的是( )
A.aa2=a2 B.(ab)3=ab3 C.(a2)3=a6 D.a10÷a2=a5
【分析】根据同底数幂的乘除运算、积的乘方以及幂的乘方运算即可求出答案.
【解答】解:A、原式=a3,故A不符合题意.
B、原式=a3b3,故B不符合题意.
C、原式=a6,故C符合题意.
D、原式=a8,故D不符合题意.
故选:C.
【点评】本题考查同底数幂的乘除运算、积的乘方以及幂的乘方运算,本题属于基础题型.
2.(2022秋 丹江口市期中)若(x+3)(x+m)展开合并后的一次项系数为﹣1,则m的值为( )
A.﹣4 B.4 C.﹣2 D.2
【分析】利用多项式乘多项式法则计算,然后根据合并后的一次项系数为﹣1,得出3+m=﹣1,然后进行计算,即可得出答案.
【解答】解:(x+3)(x+m)=x2+(3+m)x+3m,
∵(x+3)(x+m)展开合并后的一次项系数为﹣1,
∴3+m=﹣1,
∴m=﹣4.
故选:A.
【点评】此题考查了多项式乘多项式的法则,熟练掌握法则是解本题的关键.
3.(2022秋 泉州期中)已知a2﹣3a+1=0,则(a+1)(a﹣4)的值为( )
A.不确定 B.5 C.﹣3 D.﹣5
【分析】由题意可得:a2﹣3a=﹣1,再利用多项式乘多项式的法则对所求的式子进行运算,再整体代入即可.
【解答】解:∵a2﹣3a+1=0,
∴a2﹣3a=﹣1,
∴(a+1)(a﹣4)
=a2﹣4a+a﹣4
=a2﹣3a﹣4
=﹣1﹣4
=﹣5,
故选:D.
【点评】本题主要考查多项式乘多项式,整体思想,解答的关键是对相应的运算法则的掌握.
4.(2022秋 南召县期中)设A=(x﹣1)(x﹣5),B=(x﹣4)(x﹣2),则A,B的大小关系为( )
A.A>B B.A<B C.A=B D.无法确定
【分析】根据多项式乘多项式的法则先进行计算,再利用作差法比较A、B的大小,即可得出答案.
【解答】解:∵A=(x﹣1)(x﹣5),B=(x﹣2)(x﹣4),
∴A﹣B=(x﹣1)(x﹣5)﹣(x﹣2)(x﹣4)=(x2﹣6x+5)﹣(x2﹣6x+8)=﹣3<0,
∴A<B.
故选:B.
【点评】本题主要考查了多项式乘多项式,运用作差法比较大小是解题的关键.
5.(2022秋 衡南县期中)下列能使用平方差公式的是( )
A.(x+3)(x+x) B.(﹣x+y)(x﹣y)
C.(m+n)(m﹣n) D.(3m+n)(3m﹣n)
【分析】利用平方差公式的特点,完全平方公式的特点对每个选项进行分析,即可得出答案.
【解答】解:(x+3)(x+x),不符合平方差公式的特点,
∴选项A不符合题意;
∵(﹣x+y)(x﹣y)=﹣(x﹣y)2,
∴选项B不符合题意;
∵(m+n)(m﹣n)=﹣(m+n)2,不符合平方差公式的特点,
∴选项C不符合题意;
∵(3m+n)(3m﹣n),符合平方差公式的特点,
∴选项D符合题意;
故选:D.
【点评】本题考查了平方差公式,完全平方公式,掌握平方差公式的特点,完全平方公式的特点是解决问题的关键.
6.(2022秋 崇川区期中)已知:a+b=3,a﹣b=1,则a2﹣b2等于( )
A.1 B.2 C.3 D.4
【分析】根据平方差公式即可得出答案.
【解答】解:∵a+b=3,a﹣b=1,
∴原式=(a+b)(a﹣b)
=3×1
=3.
故选:C.
【点评】本题考查了平方差公式,掌握(a+b)(a﹣b)=a2﹣b2是解题的关键.
7.(2022秋 闵行区校级期中)若多项式4x2+mxy+9y2是完全平方式,则m的值为( )
A.6或﹣6 B.12或﹣12 C.12 D.﹣12
【分析】利用完全平方公式的结构特征判断即可得到m的值.
【解答】解:∵4x2+mxy+9y2是完全平方式,
∴(2x)2±2 2x 3y+(3y)2
∴mxy=±12xy,
m=±12,
故选:B.
【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
8.(2022秋 晋江市期中)计算:9992﹣998×1002=( )
A.﹣2000 B.﹣1995 C.1995 D.2000
【分析】将999转化为(1000﹣1),利用完全平方公式计算;将998写成(1000﹣2),将1002写成(1000+2),即可按照平方差公式进行计算.
【解答】解:9992﹣998×1002
=(1000﹣1)2﹣(1000﹣2)(1000+2)
=10002﹣2×1000×1+1﹣10002+4
=﹣2000+5
=﹣1995.
故选:B.
【点评】本题考查了平方差公式和完全平方公式在简便计算中的应用,熟练掌握平方差公式和完全平方公式是解题的关键.
9.(2022秋 渝北区校级期中)已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A. B. C.﹣3 D.3
【分析】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解答】解:(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b,
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴a﹣3b=0,2a﹣b=﹣5,
解得:a=﹣3,b=﹣1,
∴ab.
故选:A.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
10.(2021秋 沙坪坝区校级期末)如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中小正方形的面积为4,每个小长方形的面积为15,若用x,y分别表示小长方形的长与宽(其中xy),现给出以下关系式:①x﹣y=3;②x+y=8;③x2﹣y2=16;④x2+y2=34.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据几何意义可得,(x﹣y)2=4,xy=15,再根据整式间关系可判断每个结论的正误.
【解答】解:由题意得,(x﹣y)2=4,xy=15,
∴x﹣y2;
x+y8;
x2﹣y2=(x+y) (x﹣y)=2×8=16;
x2+y2=(x﹣y)2+2xy=4+2×15=4+30=34,
故②③④正确,
故选:C.
【点评】本题考查对完全平方公式几何意义的理解,关键是能理解完全平方公式的几何意义,去推导整式间的正确关系.
填空题(每小题3分,共24分)
12.(2022秋 晋江市期中)计算:(a6﹣2a3)÷a3= .
【分析】根据多项式除以单项式的运算法则计算即可.
【解答】解:(a6﹣2a3)÷a3
=a6÷a3﹣2a3÷a3
=a3﹣2.
故答案为:a3﹣2.
【点评】本题考查了整式的乘法,掌握多项式除以单项式的运算法则是解答本题的关键.
13.(2022秋 海安市期中)已知10a=20,100b=50,则a+2b+3= .
【分析】根据100b=50求出102b=50,根据同底数幂的乘法法则得出10a+2b=1000=103,求出a+2b=3,再求出答案即可.
【解答】解:∵100b=50,
∴(102)b=50,
∴102b=50,
∵10a=20,
∴10a×102b=20×50=1000=103,
∴10a+2b=103,
∴a+2b=3,
∴a+2b+3=3+3=6,
故答案为:6.
【点评】本题考查了幂的乘方与积的乘方和同底数幂的乘法,能求出10a+2b=103是解此题的关键.
14.(2022春 吴江区校级期中)若x2+2x=﹣1,则代数式6+x(x+2)的值为 .
【分析】利用单项式乘多项式的法则对所求的式子进行运算,再整体代入已知的条件运算即可.
【解答】解:当x2+2x=﹣1时,
6+x(x+2)
=6+(x2+2x)
=6+(﹣1)
=5.
故答案为:5.
【点评】本题主要考查单项式乘多项式,解答的关键是对相应的运算法则的掌握.
15.(2022春 新邵县期末)数学课上,老师讲了单项式与多项式相乘:先用单项式乘多项式中的每一项,再把所得的积相加,小丽在练习时,发现了这样一道题:“﹣2x2(3x﹣■+1)=﹣6x3+4x2y﹣2x2”那么“■”中的一项是 .
【分析】利用多项式除以单项式法则计算(﹣6x3+4x2y﹣2x2)÷(﹣2x2)即可得出“■”中的项,然后利用单项式乘多项式的法则进行计算验证即可.
【解答】解:∵(﹣6x3+4x2y﹣2x2)÷(﹣2x2)
=﹣6x3÷(﹣2x2)+4x2y÷(﹣2x2)﹣2x2÷(﹣2x2)
=3x﹣2y+1,
即﹣2x2(3x﹣2y+1)=﹣6x3+4x2y﹣2x2,
∴“■”中的一项是2y.
故答案为:2y.
【点评】此题考查了单项式乘多项式,熟练掌握运算法则是解本题的关键.单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
16.(2022秋 锡山区校级月考)一块长方形地长18米,如果把它的长增加到22米,宽减少3米,面积的大小正好不变,这块长方形地的面积是 平方米.
【分析】根据题意知:原来长方形的长×原长方形的宽=增加后的长×(原来的宽﹣3),据此可列出方程求出长方形的宽是多少,再根据长方形的面积公式S=ab可求出长方形的面积.
【解答】解:设原长方形的宽为x,根据题意得:
18x=22×(x﹣3),
18x=22x﹣66,
22x﹣18x=66,
4x=66,
x=16.5,
18×16.5=297(平方米),
答:这块长方形地的面积是297平方米.
故答案为:297.
【点评】此题考查了多项式乘多项式,重点是列出方程求出原来长方形的宽,再根据长方形的面积公式进行解答.
17.(2022秋 安溪县期中)若a﹣b=3,ab=﹣4,则(a+2)(b﹣2)的值为 .
【分析】先去括号,再合并同类项,最后整体代入计算即可.
【解答】解:∵(a+2)(b﹣2)
=ab﹣2(a﹣b)﹣4,
a﹣b=3,ab=﹣4,
∴原式=﹣4﹣6﹣4
=﹣14,
故答案为:﹣14.
【点评】本题主要考查了多项式乘多项式,掌握多项式与多项式相乘的法则是解题关键.
18.(2022秋 思明区校级期中)若a+b=2,则多项式a2+4b﹣b2的值是 .
【分析】把a2+4b﹣b2化为(a+b)(a﹣b)+4b的形式,再整体代入计算.
【解答】解:∵a+b=2,
∴a2+4b﹣b2
=a2﹣b2+4b
=(a+b)(a﹣b)+4b
=2(a+b)
=4,
故答案为:4.
【点评】本题考查平方差公式,掌握平方差公式的应用是解题关键.
19.(2021秋 东兴区校级期中)已知a+b=8,ab=c2+16,则a+2b+3c= .
【分析】根据已知a+b=8将等号两边平方,可得到a2+2ab+b2=64=4×16.c2+16的16看作ab﹣c2,代入移项、运用完全平方差公式转化为
(a﹣b)2+4c2=0.再根据非负数的性质与已知a+b=8,可求出a、b、c的值.代入即求得计算结果.
【解答】解:∵a+b=8
∴a2+2ab+b2=64
∵ab=c2+16
∴16=ab﹣c2
∴a2+2ab+b2=64=4×16=4(ab﹣c2)=4ab﹣4c2,即(a﹣b)2+4c2=0
∴a=b,c=0
又∵a+b=8
∴a=b=4
∴a+2b+3c=4+2×4+3×0=12
故答案为12
【点评】本题考查完全平方式与非负数的性质.同学们特别要注意我们一般是将式子用数值来代入,但对于本题是将数值16用ab﹣c2来代入.
三、解答题(共66分)
19.(每小题4分,共16分)计算:
(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3. (2)﹣(a2b)3+2a2b (﹣3a2b)2;
(3)4x(1﹣3x)+2(6x2+3x﹣1); (5)(a+2b)(a﹣2b)+(3a﹣2b)2.
【分析】(1)先算幂的乘方,再算同底数幂的乘法,最后合并同类项即可.
(2)先算乘方,后算乘法,最后算加法;
(3)根据单项式乘多项式的法则展开,合并同类项即可;
(4)根据平方差公式、完全平方公式进行化简即可求出答案.
【解答】解:(1)﹣(﹣x2)3 (﹣x2)2﹣x (﹣x3)3
=﹣(﹣x6) x4﹣x (﹣x9)
=x10+x10
=2x10.
(2)﹣(a2b)3+2a2b (﹣3a2b)2;
=﹣a6b3+2a2b 9a4b2
=﹣a6b3+18a6b3
=17a6b3;
(3)原式=4x﹣12x2+12x2+6x﹣2
=10x﹣2;
(4)原式=a2﹣4b2+9a2﹣12ab+4b2
=10a2﹣12ab.
【点评】本题主要考查整式的乘法及乘法公式,解答的关键是对相应的运算法则的掌握.
19.(5分)先化简再求值:[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y,其中x=1,y=﹣1.
【分析】原式中括号中利用平方差公式,以及完全平方公式化简,去括号合并后,利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】原式=(x2﹣4y2﹣x2﹣8xy﹣16y2)÷4y
=(﹣20y2﹣8xy)÷4y
=﹣5y﹣2x,
当x=1,y=﹣1时,原式=5﹣2=3.
【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.
20.(6分)(2022秋 南安市期中)已知(x+a)(x2﹣bx﹣1)展开后不含x的二次项,且含x的一次项系数是﹣4,求a2+b2的值.
【分析】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解答】解:(x+a)(x2﹣bx﹣1)
=x3﹣bx2﹣x+ax2﹣abx﹣a
=x3+(﹣b+a)x2+(﹣1﹣ab)x﹣a,
∵展开后不含x的二次项,且含x的一次项系数是﹣4,
∴﹣b+a=0,﹣1﹣ab=﹣4,
得:a=b,ab=3,
∴a2+b2
=(a﹣b)2+2ab
=02+2×3
=0+6
=6.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
21.(6分)(2022春 滕州市校级月考)如图,在长为3a+2,宽为2b﹣1的长方形铁片上,挖去长为2a+4,宽为b的小长方形铁片.
(1)求剩余部分面积.
(2)求出当a=3,b=2时的面积.
【分析】(1)阴影部分面积=原长方形的面积﹣挖去的长方形的面积,据此即可求解;
(2)把相应的值代入(1)运算即可.
【解答】解:(1)由题意得:
S阴影=S原长方形﹣S挖去的长方形
=(3a+2)(2b﹣1)﹣(2a+4)b
=6ab﹣3a+4b﹣2﹣2ab﹣4b
=4ab﹣3a﹣2;
(2)当a=3,b=2时,
原式=4×3×2﹣3×3﹣2
=24﹣9﹣2
=13.
【点评】本题主要考查多项式乘多项式,单项式乘多项式,解答的关键是对相应的运算法则的掌握与运用.
22.(7分)(2022春 兰溪市期中)已知:x+y=6,xy=3.求下列各式的值:
(1)x2+4xy+y2
(2)x4+y4
【分析】(1)利用完全平方公式变形可得答案;
(2)首先求出x2+y2=30,再根据完全平方公式变形可得答案.
【解答】解:(1)∵x+y=6,xy=3,
∴x2+4xy+y2
=x2+2xy+y2+2xy
=(x+y)2+2xy
=36+6
=42;
(2)∵x+y=6,xy=3,
∴x2+y2=(x+y)2﹣2xy=36﹣6=30,
∴x4+y4=(x2+y2)2﹣2x2y2
=900﹣2×9
=900﹣18
=882.
【点评】本题考查乘法公式的运用,熟练掌握完全平方公式是解题关键.
23.(8分)(2022春 东台市期中)小刚同学计算一道整式乘法:(3x+a)(2x﹣3),由于他抄错了多项式中a前面的符号,把“+”写成“﹣”,得到的结果为6x2+bx+12
(1)求a,b的值;
(2)计算这道整式乘法的正确结果.
【分析】(1)由题意得(3x﹣a)(2x﹣3)=6x2+bx+12,进而得出6x2﹣(2a+9)x+3a=6x2+bx+12,根据对应系数相等即可求出a,b的值;
(2)把a=4代入(3x+a)(2x﹣3),依据多项式乘多项式的法则进行计算,即可得出正确结果.
【解答】解:(1)由题意得:(3x﹣a)(2x﹣3)=6x2+bx+12,
∴6x2﹣(2a+9)x+3a=6x2+bx+12,
∴﹣(2a+9)=b,3a=12,
∴a=4,b=﹣17;
(2)(3x+4)(2x﹣3)
=6x2﹣9x+8x﹣12
=6x2﹣x﹣12.
【点评】本题考查了多项式乘多项式,掌握多项式乘多项式的法则是解决问题的关键.
24.(8分)(2022秋 如皋市期中)在学方差公式”时,张老师出了一道题:计算9×11×101.嘉嘉发现把9写成(10﹣1),把11写成(10+1)后可以连续运用平方差公式进行计算.
请根据上述思路,计算:
(1)9×11×101;
(2).
【分析】(1)将原式化为(10﹣1)×(10+1)×(100+1),连续利用平方差公式进行计算即可;
(2)将改写成(1)后,连续利用平方差公式进行计算即可.
【解答】解:(1)原式=(10﹣1)×(10+1)×(100+1)
=(102﹣1)×(100+1)
=(100﹣1)×(100+1)
=1002﹣1
=10000﹣1
=9999;
(2)原式=(1)×(1)×(1)×(1)×(1)
=(1)×(1)×(1)×(1)
=(1)×(1)×(1)
=(1)×(1)
=1
=1.
【点评】本题考查平方差公式,掌握平方差公式的结构特征是正确应用的前提.
25.(10分)(2022秋 吉林期中)如图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)观察图②.请你直接写出下列三个式子:(a+b)2、(a﹣b)2、ab之间的等量关系式为 ;
(2)若m、n均为实数,且m+n=﹣2,mm=﹣3,运用(1)所得到的公式求m﹣n的值;
(3)如图③,S1、S2分别表示边长为x、y的正方形的面积,且A、B、C三点在一条直线上,若S1+S2=20,AB=x+y=6,求图中阴影部分的面积.
【分析】(1)由图象中小正方形面积=大正方形面积﹣长方形面积求解.
(2)根据(m+n)2﹣(m﹣n)2=4mn求解.
(3)由xx20,x+y=6,S阴影=S△ACF+S△BCD求解.
【解答】解:(1)由图象可得:(a+b)2﹣(a﹣b)2=4ab.
故答案为:(a+b)2﹣(a﹣b)2=4ab.
(2)∵(m+n)2﹣(m﹣n)2=4mn,
∴(m﹣n)2=(m+n)2﹣4mn,
∵m+n=﹣2,mn=﹣3,
∴(m﹣n)2=(﹣2)2﹣4×(﹣3)=16.
(3)∵S1+S2=20,
∴xx20,
∴S阴影=S△ACF+S△BCDx1 x2x1 x2=x1 x2[(x1+x2)2﹣(xx)](62﹣20)=8.
【点评】本题考查完全平方式的应用,解题关键是熟练掌握完全平放式.
