生物人教版(2019)选择性必修2课件 1.2种群的数量变化(共35张ppt)
文档属性
| 名称 | 生物人教版(2019)选择性必修2课件 1.2种群的数量变化(共35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2022-11-26 20:50:52 | ||
图片预览









文档简介
(共35张PPT)
第1章 种群及其动态
第2节 种群数量的变化
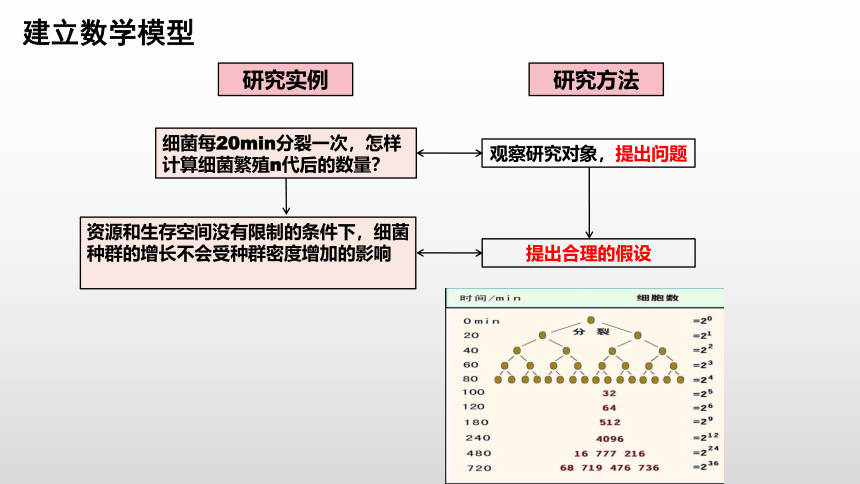
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
观察研究对象,提出问题
研究方法
研究实例
建立数学模型
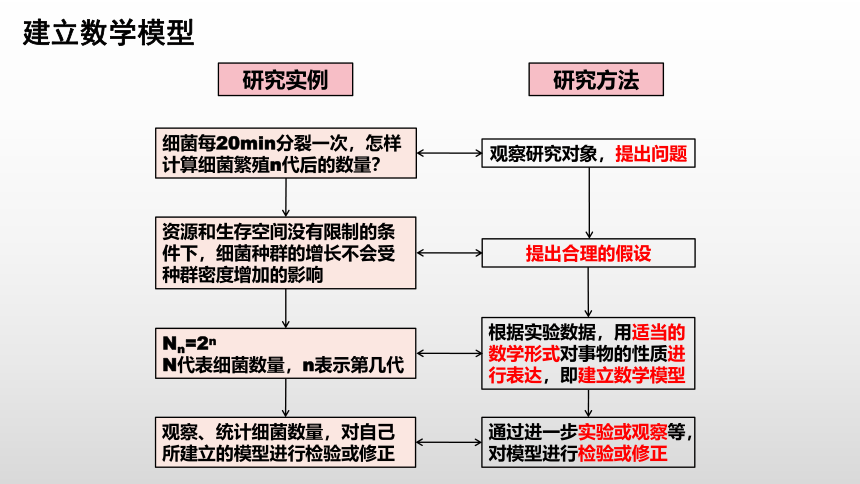
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
观察研究对象,提出问题
提出合理的假设
研究方法
研究实例
建立数学模型
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
研究方法
研究实例
建立数学模型
那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个) 2 4 8 16 32 64 128 216 512
指数形式
21
22
23
24
25
26
27
28
29
①1个细菌第n代细菌数量(Nn)的计算公式是什么?
Nn=1×2n
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
通过进一步实验或观察等,对模型进行检验或修正
研究方法
研究实例
建立数学模型
那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个) 2 4 8 16 32 64 128 216 512
指数形式
21
22
23
24
25
26
27
28
29
②初始数量为N0个细菌第n代细菌数量(Nn)的计算公式是什么?
Nn=N0×2n
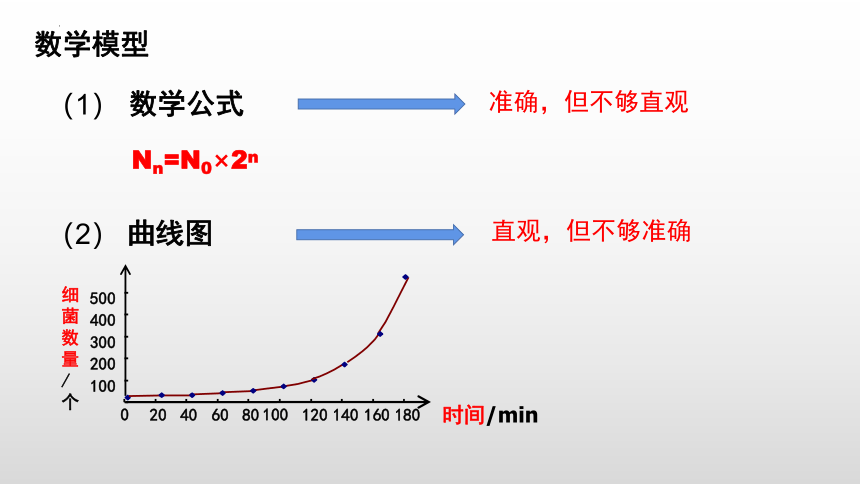
数学模型
Nn=N0×2n
(1)
数学公式
准确,但不够直观
时间/min
细
菌
数
量
/
个
0
100
200
300
400
500
20
40
60
80
100
120
140
160
180
(2)
曲线图
直观,但不够准确
思考与讨论
1.这两个资料中种群增长有什么共同点
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
种群数量增长迅猛,且呈无限增长趋势。
食物充足,缺少天敌等
不能,因食物和空间有限
一. 种群的“J” 增长
自然界有类似细菌在理想条件下种群增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”形。
*注意:
该曲线的起点不是原点。
1.模型假设(产生条件):
食物和空间条件充裕,气候适宜,没有天敌和其他竞争物种等条件下。
2.建立模型(数学公式) :
Nt=N0λt
t年后种群的数量为:
(N0为起始数量, t为时间,Nt表示t年后该种群的数量,λ表示该种群数量是一年前种群数量的倍数。)
λ>1且恒定
3. 实例
①生物迁入适宜其生活的新环境后,一段时间内种群的数量变化;
②实验室条件。
增长率与增长速率
增长率:在单位时间内净增加的个体数占个体总数的比率 :
增长率 增长速率
增长率=增长数量/初始数量
=(Nt+1—Nt)/ Nt
= λ-1(定值)
增长速率:指单位时间种群增长数量:
增长速率=
增长数量/时间
= (Nt+1—Nt)/ 时间
=曲线的斜率
4.“J”型曲线特征
“J”型曲线特征:
____最大值,__________和_______是不变的, ________不断增加。
无
增长倍数(λ) 增长率
增长速率
种群数量
时间
增长率
时间
λ-1
增长速率
时间
5.有关λ的典型曲线解读
λ≠增长率
λ为某时段结束时种群数量为初始数量的倍数
增长率=λ-1
二. 种群的“S”形 增长
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形
1、产生原因:资源和空间有限,种内竞争加剧
ab段:
bc段:
cd段:
de段:
种群基数小,需要适应新环境,增长较缓慢;
资源和空间丰富,出生率升高,种群数量增长迅速;
资源和空间有限。当种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓;
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。种群数量达到最大,且种内斗争最剧
种内竞争对种群数量起调节作用
2.“S”型曲线
概念:
一定的环境条件所能维持的种群最大数量称为环境容纳量
特点:
出生率≈死亡率,种群增长速率为0
关于K值
1.种群数量到达K值后就不再变化了吗?
种群数量达到K值并不是一成不变的,而是围绕K值上下波动
2.K值是不是种群数量的最大值?
不是;种群数量能达到的最大值是种群数量在某一时间点出现的最大值,这个值存在的时间很短,可以大于K值
3.同一种群的K值是固定不变的吗?
大熊猫栖息地遭到破坏后,由于食物的减少和活动范围的缩小,其K值就会变小。这是野生大熊猫种群数量锐减的重要原因。因此,建立自然保护区,给大熊猫更宽广的生存空间,改善它们的栖息环境,从而提高环境容纳量,是保护大熊猫的根本措施
K值不是一成不变的。会受到环境的影响,环境遭受破坏,K值会下降;环境改善时,K值会上升
K/2
a
b
c
g
h
f
e
甲
乙
3“S”型曲线特征
4.K值的不同表示方法
K值:
A.B.C.D
K/2 值
A'.C'.D'
增长类型 “J”型 “S”型
增长率
增长速率
总结
思考与讨论
环境容纳量与现实生活
2.鼠害导致作物减产,蚊,蝇会传播疾病。从环境容纳量的角度思考,对家鼠等有害动物的控制,应当采取什么措施
降低有害动物的环境容纳量
将粮食和其他食物存储在安全处,断绝或减少它们的食物来源
室内采取硬化地面等措施,减少它们挖造巢穴的场所
养殖或释放它们的天敌
搞好环境卫生
三. 种群数量的波动
(1)在自然界,有的种群能够在一段时间内维持数量的相对稳定。
(2)但大多数生物的种群来说,种群数量总是在波动中。
东亚飞蝗种群数量的波动
(3) 种群数量波动产生的影响
影响结果 原因分析 实例
易成灾
种群处于波动状态,说明制约其种群数量变化的因素较少或也处于不稳定中,在某些特定条件下可能出现种群爆发
蝗灾、鼠灾、赤潮等是种群数量爆发增长的结果
种群的延长需要有一定的个体数量为基础,当一个种群的数量过少,种群可能会由于近亲繁殖等原因而衰退、消亡
有的鲸濒临灭绝、大熊猫等珍稀动物不加强保护也极易灭绝
(不利条件)
易消亡
核心点二 探究培养液中酵母菌种群数量的变化
1.实验原理
(1)酵母菌属于兼性厌氧型微生物,有氧呼吸时产生二氧化碳和水,无氧呼吸时产生二氧化碳和酒精。
(2)用液体培养基(培养液)培养酵母菌,种群的增长受培养液的成分、空间、pH、温度等因素的影响。
(3)在理想的环境中,酵母菌种群数量呈“J”形增长;在资源和空间有限的环境下,酵母菌种群数量呈“S”形增长。
2.实验步骤
计数室
计数室(中间大方格)的长和宽各为1mm,深度为0.1mm,其体积为______mm3 ,合_________mL。
1mm
0.1
1×10-4
3.血细胞计数板的使用:
放大
1
4
9
10
11
12
13
14
15
16
5
2
3
6
7
8
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
22
23
24
25
共400个小方格
共400个小方格
计数4个中方格,100个小方格
计数5个中方格,80个小方格
4.计算公式
25×16型
酵母菌的种群密度=中方格中酵母菌数量的平均值×25×104×稀释倍数
16×25型
酵母菌的种群密度=中方格中酵母菌数量的平均值×16×104×稀释倍数
(1)酵母菌的计数方法:抽样检测
(2)先将盖玻片放在计数室上,再滴加培养液在盖玻片的边缘(若先滴加培养液,再盖盖玻片,导致计数结果偏高)
(3)取样前为什么轻轻振荡试管?
使酵母菌分布均匀,取样准确
(4)如果一个小方格中酵母菌过多不便计数,怎么办?
先稀释培养液,再取样计数
(5)对于压在小方格界线上的酵母菌,应当怎样计数?
类似“样方法”处理
(6)本探究需要另外设置对照组吗?
无需,自身前后对照
(7)需要做重复实验吗?
需要重复,提高准确率
第一天 第二天 第三天 第四天 第五天 第六天
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
每个方格菌数 1
2
3
4
5
稀释 倍数
平均值
总平 均值
如何更直观的显示出实验结果?
5记录表格设计示例:
——曲线图
活菌数
6实验结果与分析
(1)酵母菌增长曲线图
食物和空间充裕,出生率>死亡率
空间资源有限。种群密度增大,种内竞争加剧,出生率≈死亡率
营养消耗、pH变化、有害产物积累,出生率<死亡率
(2)趋势:先增加后减少。
(3)局限:无法区分细胞死活,计数值比实际值偏大
第1章 种群及其动态
第2节 种群数量的变化
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
观察研究对象,提出问题
研究方法
研究实例
建立数学模型
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
观察研究对象,提出问题
提出合理的假设
研究方法
研究实例
建立数学模型
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
研究方法
研究实例
建立数学模型
那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个) 2 4 8 16 32 64 128 216 512
指数形式
21
22
23
24
25
26
27
28
29
①1个细菌第n代细菌数量(Nn)的计算公式是什么?
Nn=1×2n
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
通过进一步实验或观察等,对模型进行检验或修正
研究方法
研究实例
建立数学模型
那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个) 2 4 8 16 32 64 128 216 512
指数形式
21
22
23
24
25
26
27
28
29
②初始数量为N0个细菌第n代细菌数量(Nn)的计算公式是什么?
Nn=N0×2n
数学模型
Nn=N0×2n
(1)
数学公式
准确,但不够直观
时间/min
细
菌
数
量
/
个
0
100
200
300
400
500
20
40
60
80
100
120
140
160
180
(2)
曲线图
直观,但不够准确
思考与讨论
1.这两个资料中种群增长有什么共同点
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
种群数量增长迅猛,且呈无限增长趋势。
食物充足,缺少天敌等
不能,因食物和空间有限
一. 种群的“J” 增长
自然界有类似细菌在理想条件下种群增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”形。
*注意:
该曲线的起点不是原点。
1.模型假设(产生条件):
食物和空间条件充裕,气候适宜,没有天敌和其他竞争物种等条件下。
2.建立模型(数学公式) :
Nt=N0λt
t年后种群的数量为:
(N0为起始数量, t为时间,Nt表示t年后该种群的数量,λ表示该种群数量是一年前种群数量的倍数。)
λ>1且恒定
3. 实例
①生物迁入适宜其生活的新环境后,一段时间内种群的数量变化;
②实验室条件。
增长率与增长速率
增长率:在单位时间内净增加的个体数占个体总数的比率 :
增长率 增长速率
增长率=增长数量/初始数量
=(Nt+1—Nt)/ Nt
= λ-1(定值)
增长速率:指单位时间种群增长数量:
增长速率=
增长数量/时间
= (Nt+1—Nt)/ 时间
=曲线的斜率
4.“J”型曲线特征
“J”型曲线特征:
____最大值,__________和_______是不变的, ________不断增加。
无
增长倍数(λ) 增长率
增长速率
种群数量
时间
增长率
时间
λ-1
增长速率
时间
5.有关λ的典型曲线解读
λ≠增长率
λ为某时段结束时种群数量为初始数量的倍数
增长率=λ-1
二. 种群的“S”形 增长
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形
1、产生原因:资源和空间有限,种内竞争加剧
ab段:
bc段:
cd段:
de段:
种群基数小,需要适应新环境,增长较缓慢;
资源和空间丰富,出生率升高,种群数量增长迅速;
资源和空间有限。当种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓;
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。种群数量达到最大,且种内斗争最剧
种内竞争对种群数量起调节作用
2.“S”型曲线
概念:
一定的环境条件所能维持的种群最大数量称为环境容纳量
特点:
出生率≈死亡率,种群增长速率为0
关于K值
1.种群数量到达K值后就不再变化了吗?
种群数量达到K值并不是一成不变的,而是围绕K值上下波动
2.K值是不是种群数量的最大值?
不是;种群数量能达到的最大值是种群数量在某一时间点出现的最大值,这个值存在的时间很短,可以大于K值
3.同一种群的K值是固定不变的吗?
大熊猫栖息地遭到破坏后,由于食物的减少和活动范围的缩小,其K值就会变小。这是野生大熊猫种群数量锐减的重要原因。因此,建立自然保护区,给大熊猫更宽广的生存空间,改善它们的栖息环境,从而提高环境容纳量,是保护大熊猫的根本措施
K值不是一成不变的。会受到环境的影响,环境遭受破坏,K值会下降;环境改善时,K值会上升
K/2
a
b
c
g
h
f
e
甲
乙
3“S”型曲线特征
4.K值的不同表示方法
K值:
A.B.C.D
K/2 值
A'.C'.D'
增长类型 “J”型 “S”型
增长率
增长速率
总结
思考与讨论
环境容纳量与现实生活
2.鼠害导致作物减产,蚊,蝇会传播疾病。从环境容纳量的角度思考,对家鼠等有害动物的控制,应当采取什么措施
降低有害动物的环境容纳量
将粮食和其他食物存储在安全处,断绝或减少它们的食物来源
室内采取硬化地面等措施,减少它们挖造巢穴的场所
养殖或释放它们的天敌
搞好环境卫生
三. 种群数量的波动
(1)在自然界,有的种群能够在一段时间内维持数量的相对稳定。
(2)但大多数生物的种群来说,种群数量总是在波动中。
东亚飞蝗种群数量的波动
(3) 种群数量波动产生的影响
影响结果 原因分析 实例
易成灾
种群处于波动状态,说明制约其种群数量变化的因素较少或也处于不稳定中,在某些特定条件下可能出现种群爆发
蝗灾、鼠灾、赤潮等是种群数量爆发增长的结果
种群的延长需要有一定的个体数量为基础,当一个种群的数量过少,种群可能会由于近亲繁殖等原因而衰退、消亡
有的鲸濒临灭绝、大熊猫等珍稀动物不加强保护也极易灭绝
(不利条件)
易消亡
核心点二 探究培养液中酵母菌种群数量的变化
1.实验原理
(1)酵母菌属于兼性厌氧型微生物,有氧呼吸时产生二氧化碳和水,无氧呼吸时产生二氧化碳和酒精。
(2)用液体培养基(培养液)培养酵母菌,种群的增长受培养液的成分、空间、pH、温度等因素的影响。
(3)在理想的环境中,酵母菌种群数量呈“J”形增长;在资源和空间有限的环境下,酵母菌种群数量呈“S”形增长。
2.实验步骤
计数室
计数室(中间大方格)的长和宽各为1mm,深度为0.1mm,其体积为______mm3 ,合_________mL。
1mm
0.1
1×10-4
3.血细胞计数板的使用:
放大
1
4
9
10
11
12
13
14
15
16
5
2
3
6
7
8
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
22
23
24
25
共400个小方格
共400个小方格
计数4个中方格,100个小方格
计数5个中方格,80个小方格
4.计算公式
25×16型
酵母菌的种群密度=中方格中酵母菌数量的平均值×25×104×稀释倍数
16×25型
酵母菌的种群密度=中方格中酵母菌数量的平均值×16×104×稀释倍数
(1)酵母菌的计数方法:抽样检测
(2)先将盖玻片放在计数室上,再滴加培养液在盖玻片的边缘(若先滴加培养液,再盖盖玻片,导致计数结果偏高)
(3)取样前为什么轻轻振荡试管?
使酵母菌分布均匀,取样准确
(4)如果一个小方格中酵母菌过多不便计数,怎么办?
先稀释培养液,再取样计数
(5)对于压在小方格界线上的酵母菌,应当怎样计数?
类似“样方法”处理
(6)本探究需要另外设置对照组吗?
无需,自身前后对照
(7)需要做重复实验吗?
需要重复,提高准确率
第一天 第二天 第三天 第四天 第五天 第六天
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
每个方格菌数 1
2
3
4
5
稀释 倍数
平均值
总平 均值
如何更直观的显示出实验结果?
5记录表格设计示例:
——曲线图
活菌数
6实验结果与分析
(1)酵母菌增长曲线图
食物和空间充裕,出生率>死亡率
空间资源有限。种群密度增大,种内竞争加剧,出生率≈死亡率
营养消耗、pH变化、有害产物积累,出生率<死亡率
(2)趋势:先增加后减少。
(3)局限:无法区分细胞死活,计数值比实际值偏大
