五年级上册数学第六单元 多边形面积 基础训练卷(含答案)
文档属性
| 名称 | 五年级上册数学第六单元 多边形面积 基础训练卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 235.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 20:11:33 | ||
图片预览


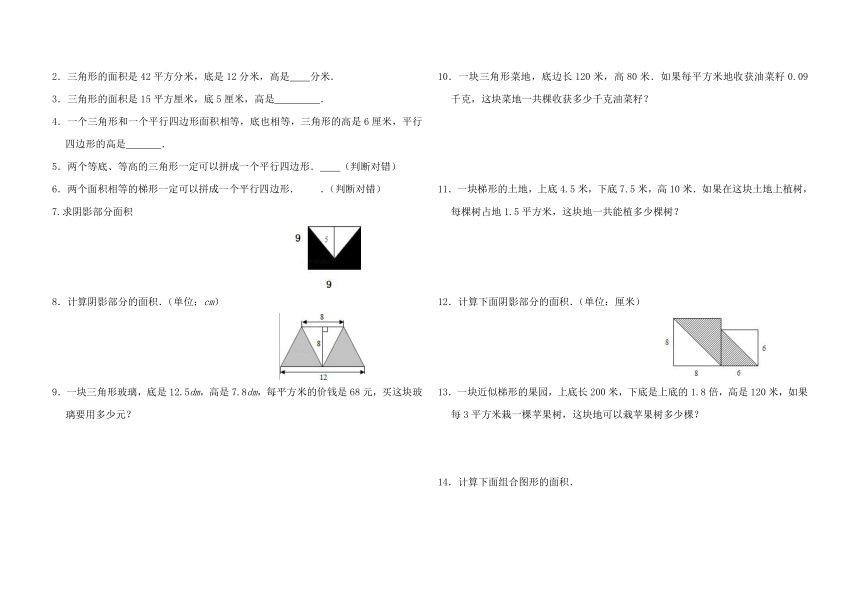
文档简介
五年级上册数学第六单元 多边形面积 基础训练卷
知识点一、面积公式应用
例1.一个平行四边形的底是2.6厘米,高是4厘米,面积是 ,
一个三角形的底是2.5厘米,面积是10平方厘米,高是 .
例2、 一个平行四边形相邻两条边分别是6厘米、4厘米,量得一条边上的高为5厘米,这个平行四边形的面积是( )平方厘米。
例3、一个直角三角形的三条边分别是10厘米,6厘米和8厘米,这个三角形的面积是 平方厘米,斜边上的高是 厘米.
例4.一个平行四边形的底是10厘米,高6.4厘米,与它等底等高的三角形的面积是 平方厘米.
例5.两个完全一样的梯形可以拼成一个 ,拼成图形的底等于梯形的 ,拼成图形的高等于梯形的 .
例6.如果用S表示梯形的面积,a、b分别表示上底和下底,那么它的高是( )
A.S÷2÷(a+bB.S×2×(a+b) C.2S÷(a+b) D.S÷2(a+b)
例7.一个直角梯形的上底是9㎝,下底是11㎝,高是9㎝,它的面积是( )㎝ ,在梯形内剪下一个最大的正方形,正方形的面积是( )㎝ 。
例8.如图是阴影部分的面积相比较( )
A.甲>乙 B.甲<乙 C.相等
知识点二、三角形与平行四边形面积之间的关系
例1.三角形的面积大小与它的底和高有关. .(判断对错)
例2.平行四边形的面积等于三角形面积的2倍. .(判断对错)
例3.两个面积相等的梯形,一定能拼成一个平行四边形. .(判断对错)
例4.三角形的底越大,面积就越大. (判断对错)
例5.若平行四边形和三角形的面积相等,底也相等,平行四边形的高是8,那么三角形的高是4. .(判断对错)
例6.两个三角形与一个平行四边形的底相等,面积也相等.平行四边形的高是3厘米,三角形的高是( )厘米.
A.1.5 B.3 C.6 D.9
例7.一个三角形与一个平行四边形的面积相等,底也相等.三角形的高是2分米,平行四边形的高是( )分米.
A.1 B.2 C.4
例8.一个平行四边形和一个三角形的高相等,面积也相等,已知平行四边形的底是4厘米,那么三角形的底是( )厘米.
A.4 B.8 C.2
例9.如图,阴影部分的面积是12㎝ ,则平行四边形的面积是( )㎝ 。
例10.在右面的平行四边形中,阴影部分和空白部分的面积相比较,下面说法正确的是( )。
A.阴影部分面积大 B.空白部分面积大
C.一样大 D.无法确定
知识点三、面积的变化规律
例1.平行四边形的高和底都缩小到原来的,面积也会缩小到原来的. .(判断对错)
例2.三角形的底和高都扩大4倍,它的面积就扩大( )倍.
A.4 B.8 C.16
例3.一个平行四边形,底扩大到原来的3倍,高扩大到原来的4倍,面积( )
A.扩大到原来的12倍 B.不变
C.扩大到原来的7倍
例4.一个梯形的上底、下底、高分别扩大2倍,它的面积扩大( )倍.
A.2 B.4 C.6 D.8
知识点四、长方形与平行四边形之间的关系
例1.把一个长方形拉成一个一般平行四边形,比较它们的面积结果是( )
A.相等 B.长方形面积大
C.平行四边形面积大
例2.把一个平行四边形拉成一个长方形,它的面积( )
A.比原来大 B.比原来小 C.没变 D.无法比较
例3.把一根铁丝围成的长方形拉成平行四边形,它的( )不变.
A.面积 B.周长 C.面积和周长 D.高
例4.图中正方形ABCD的周长是24dm,求出平行四边形CDEF的面积。
知识点五、实际应用
例1.操作及图形计算.在下面的梯形中剪去一个最大的三角形(剩下独立的一部分),剩下的面积是多少?(用虚线表示剪的痕迹)
例2.计算下面各图的面积.(单位:cm)
例3.在一张长17厘米、宽5厘米的长方形纸上,要剪出边长为2厘米的正方形,最多剪出这样的正方形几个?
例4.下图是墙面示意图,砌这面墙平均每平方米用砖160块,一共用砖多少块?
课后作业:
1.一个平行四边形的底是10分米,高6分米,面积是 平方分米,与它等底等高的三角形面积是 平方分米.
2.三角形的面积是42平方分米,底是12分米,高是 分米.
3.三角形的面积是15平方厘米,底5厘米,高是 .
4.一个三角形和一个平行四边形面积相等,底也相等,三角形的高是6厘米,平行四边形的高是 .
5.两个等底、等高的三角形一定可以拼成一个平行四边形. (判断对错)
6.两个面积相等的梯形一定可以拼成一个平行四边形. .(判断对错)
7.求阴影部分面积
8.计算阴影部分的面积.(单位:cm)
9.一块三角形玻璃,底是12.5dm,高是7.8dm,每平方米的价钱是68元,买这块玻璃要用多少元?
10.一块三角形菜地,底边长120米,高80米.如果每平方米地收获油菜籽0.09千克,这块菜地一共棵收获多少千克油菜籽?
11.一块梯形的土地,上底4.5米,下底7.5米,高10米.如果在这块土地上植树,每棵树占地1.5平方米,这块地一共能植多少棵树?
12.计算下面阴影部分的面积.(单位:厘米)
13.一块近似梯形的果园,上底长200米,下底是上底的1.8倍,高是120米,如果每3平方米栽一棵苹果树,这块地可以栽苹果树多少棵?
14.计算下面组合图形的面积.
15.一块梯形广告牌,上底是4m,下底是8.5m,高是6.4m.如果要油饰这块广告牌,每平方米用油漆0.6kg,共需要多少千克油漆?
答案:
知识点一、面积公式应用
例1.答案:10.4平方厘米 /8厘米
例2、答案:20
例3、【解答】解:三角形的面积:6×8÷2
=48÷2
=24(平方厘米);
斜边上的高:24×2÷10
=48÷10
=4.8(厘米);
答:这个三角形的面积是24平方厘米;斜边上的高是4.8厘米.
故答案为:24,4.8.
例4.答案:32
例5.答案:平行四边形/ 上下底之和/高
例6.故选:C.
例7.答案:90,81
例8.故答案为:C.
知识点二、三角形与平行四边形面积之间的关系
例1.故答案为:正确
例2.故答案为:×
例3.故答案为:×
例4.故答案为:×
例5.故答案为:×
例6.故答案为:C.
例7.故选:A.
例8.故选:B.
例9.答案:24
例10.答案:C
知识点三、面积的变化规律
例1.故答案为:×
例2.故选:C.
例3.故答案为:A
例4.故选:B.
知识点四、长方形与平行四边形之间的关系
例1.故答案为:B
例2.故答案为:A.
例3.故选:B.
例4.答案:36平方分米
知识点五、实际应用
例1.(16+8.8)×7÷2﹣16×7÷2
=24.8×7÷2﹣56
=86.8﹣56
=30.8(平方厘米),
答:剩下的面积是30.8平方厘米.
例2.【解答】解:
(3.2+4.8)×3.3÷2+3.2×3.5÷2
=8×3.3÷2+11.2÷2
=13.2+5.6
=18.8(平方厘米)
答:图形的面积是18.8平方厘米.
例3.【解答】解:17÷2=8(条)…1(厘米)
5÷2=2(条)…1(厘米)
8×2=16(个)
答:最多剪出这样的正方形16个.
【点评】本题的重点是求出各条边上能剪几个长2厘米的线段再进行解答.
例4.答案:40.6平方米;6496块
课后作业:
1.故答案为:60,30.
2.故答案为:7
3.答案:6厘米
4.故答案为:3厘米.
5.故答案为:×
6.故答案为:×
7.【解答】解:9×9﹣9×5÷2
=81﹣22.5
=58.5
答:阴影部分面积是58.5
8.【解答】解:(8+12)×8÷2﹣8×8÷2
=20×8÷2﹣32
=80﹣32
=48(平方厘米)
答:阴影部分的面积是48平方厘米.
9.【解答】解:12.5×7.8÷2÷100×68,
=97.5÷2÷100×68,
=48.75÷100×68,
=33.15(元);
答:买这块玻璃需要33.15元.
10.【解答】解:120×80÷2×0.09
=4800×0.09
=432(千克),
答:这块菜地一共棵收获432千克油菜籽.
11.【解答】解:(4.5+7.5)×10÷2÷1.5
=12×10÷2÷1.5
=120÷2÷1.5
=60÷1.5
=40(棵)
答:这块地一共能植40棵树.
12.【解答】解:8×8÷2+6×6÷2
=32+18
=50(平方厘米)
答:阴影部分的面积等于42平方厘米.
13.【分析】首先根据梯形的面积公式:s=(a+b)×h÷2,求出这个果园的面积,再用果园的面积除以3就是栽的棵数.
【解答】解:200×1.8=360(米)
(200+360)×120÷2÷3
=560×120÷2÷3
=33600÷3
=11200(棵);
答:这块果园可以栽11200棵果树.
14.【解答】解:6.5×5+(4+8)×5÷2
=32.5+12×5÷2
=32.5+30
=62.5(平方厘米)
答:组合图形的面积为62.5平方厘米.
15.【分析】先求出这个梯形的面积,然后再用该面积乘0.6千克就是一共需要多少千克油漆的质量.
【解答】解:(4+8.5)×6.4÷2×0.6
=12.5×6.4÷2×0.6
=40×0.6
=24(千克)
答:共需要24千克油漆.
知识点一、面积公式应用
例1.一个平行四边形的底是2.6厘米,高是4厘米,面积是 ,
一个三角形的底是2.5厘米,面积是10平方厘米,高是 .
例2、 一个平行四边形相邻两条边分别是6厘米、4厘米,量得一条边上的高为5厘米,这个平行四边形的面积是( )平方厘米。
例3、一个直角三角形的三条边分别是10厘米,6厘米和8厘米,这个三角形的面积是 平方厘米,斜边上的高是 厘米.
例4.一个平行四边形的底是10厘米,高6.4厘米,与它等底等高的三角形的面积是 平方厘米.
例5.两个完全一样的梯形可以拼成一个 ,拼成图形的底等于梯形的 ,拼成图形的高等于梯形的 .
例6.如果用S表示梯形的面积,a、b分别表示上底和下底,那么它的高是( )
A.S÷2÷(a+bB.S×2×(a+b) C.2S÷(a+b) D.S÷2(a+b)
例7.一个直角梯形的上底是9㎝,下底是11㎝,高是9㎝,它的面积是( )㎝ ,在梯形内剪下一个最大的正方形,正方形的面积是( )㎝ 。
例8.如图是阴影部分的面积相比较( )
A.甲>乙 B.甲<乙 C.相等
知识点二、三角形与平行四边形面积之间的关系
例1.三角形的面积大小与它的底和高有关. .(判断对错)
例2.平行四边形的面积等于三角形面积的2倍. .(判断对错)
例3.两个面积相等的梯形,一定能拼成一个平行四边形. .(判断对错)
例4.三角形的底越大,面积就越大. (判断对错)
例5.若平行四边形和三角形的面积相等,底也相等,平行四边形的高是8,那么三角形的高是4. .(判断对错)
例6.两个三角形与一个平行四边形的底相等,面积也相等.平行四边形的高是3厘米,三角形的高是( )厘米.
A.1.5 B.3 C.6 D.9
例7.一个三角形与一个平行四边形的面积相等,底也相等.三角形的高是2分米,平行四边形的高是( )分米.
A.1 B.2 C.4
例8.一个平行四边形和一个三角形的高相等,面积也相等,已知平行四边形的底是4厘米,那么三角形的底是( )厘米.
A.4 B.8 C.2
例9.如图,阴影部分的面积是12㎝ ,则平行四边形的面积是( )㎝ 。
例10.在右面的平行四边形中,阴影部分和空白部分的面积相比较,下面说法正确的是( )。
A.阴影部分面积大 B.空白部分面积大
C.一样大 D.无法确定
知识点三、面积的变化规律
例1.平行四边形的高和底都缩小到原来的,面积也会缩小到原来的. .(判断对错)
例2.三角形的底和高都扩大4倍,它的面积就扩大( )倍.
A.4 B.8 C.16
例3.一个平行四边形,底扩大到原来的3倍,高扩大到原来的4倍,面积( )
A.扩大到原来的12倍 B.不变
C.扩大到原来的7倍
例4.一个梯形的上底、下底、高分别扩大2倍,它的面积扩大( )倍.
A.2 B.4 C.6 D.8
知识点四、长方形与平行四边形之间的关系
例1.把一个长方形拉成一个一般平行四边形,比较它们的面积结果是( )
A.相等 B.长方形面积大
C.平行四边形面积大
例2.把一个平行四边形拉成一个长方形,它的面积( )
A.比原来大 B.比原来小 C.没变 D.无法比较
例3.把一根铁丝围成的长方形拉成平行四边形,它的( )不变.
A.面积 B.周长 C.面积和周长 D.高
例4.图中正方形ABCD的周长是24dm,求出平行四边形CDEF的面积。
知识点五、实际应用
例1.操作及图形计算.在下面的梯形中剪去一个最大的三角形(剩下独立的一部分),剩下的面积是多少?(用虚线表示剪的痕迹)
例2.计算下面各图的面积.(单位:cm)
例3.在一张长17厘米、宽5厘米的长方形纸上,要剪出边长为2厘米的正方形,最多剪出这样的正方形几个?
例4.下图是墙面示意图,砌这面墙平均每平方米用砖160块,一共用砖多少块?
课后作业:
1.一个平行四边形的底是10分米,高6分米,面积是 平方分米,与它等底等高的三角形面积是 平方分米.
2.三角形的面积是42平方分米,底是12分米,高是 分米.
3.三角形的面积是15平方厘米,底5厘米,高是 .
4.一个三角形和一个平行四边形面积相等,底也相等,三角形的高是6厘米,平行四边形的高是 .
5.两个等底、等高的三角形一定可以拼成一个平行四边形. (判断对错)
6.两个面积相等的梯形一定可以拼成一个平行四边形. .(判断对错)
7.求阴影部分面积
8.计算阴影部分的面积.(单位:cm)
9.一块三角形玻璃,底是12.5dm,高是7.8dm,每平方米的价钱是68元,买这块玻璃要用多少元?
10.一块三角形菜地,底边长120米,高80米.如果每平方米地收获油菜籽0.09千克,这块菜地一共棵收获多少千克油菜籽?
11.一块梯形的土地,上底4.5米,下底7.5米,高10米.如果在这块土地上植树,每棵树占地1.5平方米,这块地一共能植多少棵树?
12.计算下面阴影部分的面积.(单位:厘米)
13.一块近似梯形的果园,上底长200米,下底是上底的1.8倍,高是120米,如果每3平方米栽一棵苹果树,这块地可以栽苹果树多少棵?
14.计算下面组合图形的面积.
15.一块梯形广告牌,上底是4m,下底是8.5m,高是6.4m.如果要油饰这块广告牌,每平方米用油漆0.6kg,共需要多少千克油漆?
答案:
知识点一、面积公式应用
例1.答案:10.4平方厘米 /8厘米
例2、答案:20
例3、【解答】解:三角形的面积:6×8÷2
=48÷2
=24(平方厘米);
斜边上的高:24×2÷10
=48÷10
=4.8(厘米);
答:这个三角形的面积是24平方厘米;斜边上的高是4.8厘米.
故答案为:24,4.8.
例4.答案:32
例5.答案:平行四边形/ 上下底之和/高
例6.故选:C.
例7.答案:90,81
例8.故答案为:C.
知识点二、三角形与平行四边形面积之间的关系
例1.故答案为:正确
例2.故答案为:×
例3.故答案为:×
例4.故答案为:×
例5.故答案为:×
例6.故答案为:C.
例7.故选:A.
例8.故选:B.
例9.答案:24
例10.答案:C
知识点三、面积的变化规律
例1.故答案为:×
例2.故选:C.
例3.故答案为:A
例4.故选:B.
知识点四、长方形与平行四边形之间的关系
例1.故答案为:B
例2.故答案为:A.
例3.故选:B.
例4.答案:36平方分米
知识点五、实际应用
例1.(16+8.8)×7÷2﹣16×7÷2
=24.8×7÷2﹣56
=86.8﹣56
=30.8(平方厘米),
答:剩下的面积是30.8平方厘米.
例2.【解答】解:
(3.2+4.8)×3.3÷2+3.2×3.5÷2
=8×3.3÷2+11.2÷2
=13.2+5.6
=18.8(平方厘米)
答:图形的面积是18.8平方厘米.
例3.【解答】解:17÷2=8(条)…1(厘米)
5÷2=2(条)…1(厘米)
8×2=16(个)
答:最多剪出这样的正方形16个.
【点评】本题的重点是求出各条边上能剪几个长2厘米的线段再进行解答.
例4.答案:40.6平方米;6496块
课后作业:
1.故答案为:60,30.
2.故答案为:7
3.答案:6厘米
4.故答案为:3厘米.
5.故答案为:×
6.故答案为:×
7.【解答】解:9×9﹣9×5÷2
=81﹣22.5
=58.5
答:阴影部分面积是58.5
8.【解答】解:(8+12)×8÷2﹣8×8÷2
=20×8÷2﹣32
=80﹣32
=48(平方厘米)
答:阴影部分的面积是48平方厘米.
9.【解答】解:12.5×7.8÷2÷100×68,
=97.5÷2÷100×68,
=48.75÷100×68,
=33.15(元);
答:买这块玻璃需要33.15元.
10.【解答】解:120×80÷2×0.09
=4800×0.09
=432(千克),
答:这块菜地一共棵收获432千克油菜籽.
11.【解答】解:(4.5+7.5)×10÷2÷1.5
=12×10÷2÷1.5
=120÷2÷1.5
=60÷1.5
=40(棵)
答:这块地一共能植40棵树.
12.【解答】解:8×8÷2+6×6÷2
=32+18
=50(平方厘米)
答:阴影部分的面积等于42平方厘米.
13.【分析】首先根据梯形的面积公式:s=(a+b)×h÷2,求出这个果园的面积,再用果园的面积除以3就是栽的棵数.
【解答】解:200×1.8=360(米)
(200+360)×120÷2÷3
=560×120÷2÷3
=33600÷3
=11200(棵);
答:这块果园可以栽11200棵果树.
14.【解答】解:6.5×5+(4+8)×5÷2
=32.5+12×5÷2
=32.5+30
=62.5(平方厘米)
答:组合图形的面积为62.5平方厘米.
15.【分析】先求出这个梯形的面积,然后再用该面积乘0.6千克就是一共需要多少千克油漆的质量.
【解答】解:(4+8.5)×6.4÷2×0.6
=12.5×6.4÷2×0.6
=40×0.6
=24(千克)
答:共需要24千克油漆.
