苏科版九年级数学下册7.1 正切 课件(共22张PPT)
文档属性
| 名称 | 苏科版九年级数学下册7.1 正切 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 307.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 21:32:44 | ||
图片预览


文档简介
(共22张PPT)
7.1 正切
A
C
B
D
设疑自探
设疑自探
A
C
B
D
更陡!
8米
12米
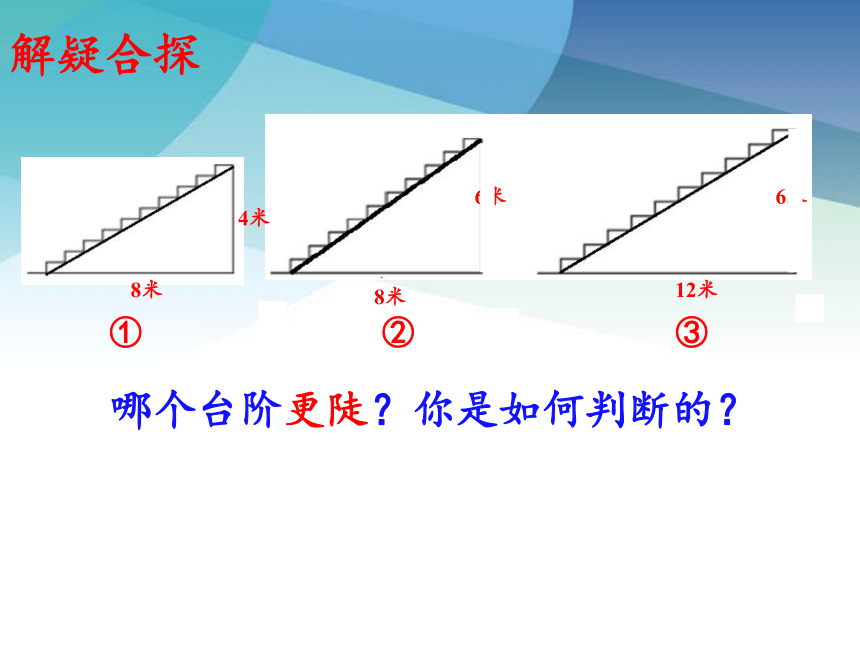
6米
6米
8米
4米
解疑合探
哪个台阶更陡?你是如何判断的?
①
③
②
8
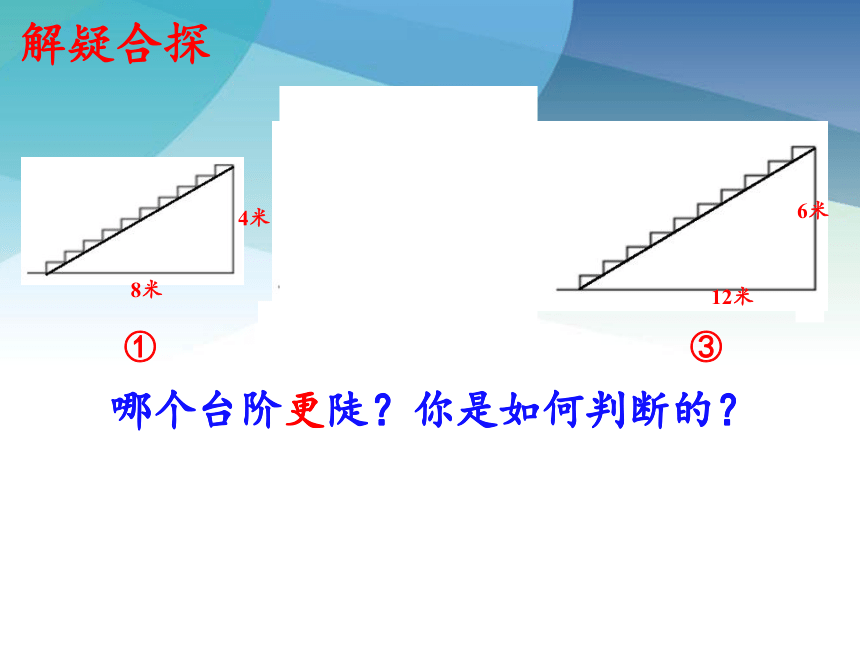
12米
6
6米
8米
4米
①
③
②
解疑合探
哪个台阶更陡?你是如何判断的?
哪个台阶更陡?你是如何判断的?
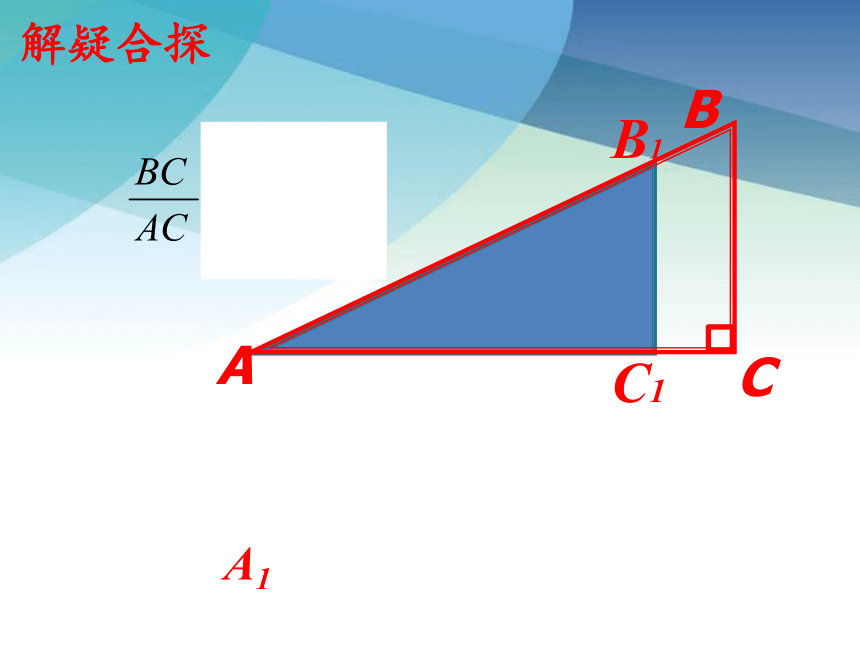
B1
C1
A
B
C
解疑合探
A1
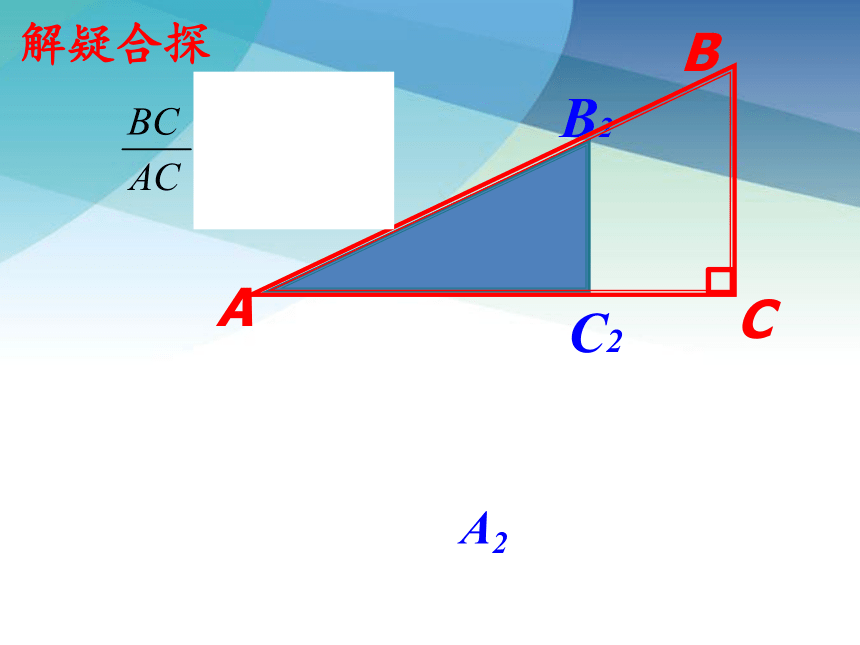
B2
C2
A
B
C
解疑合探
A2
B1
C1
A
B
C
B2
C2
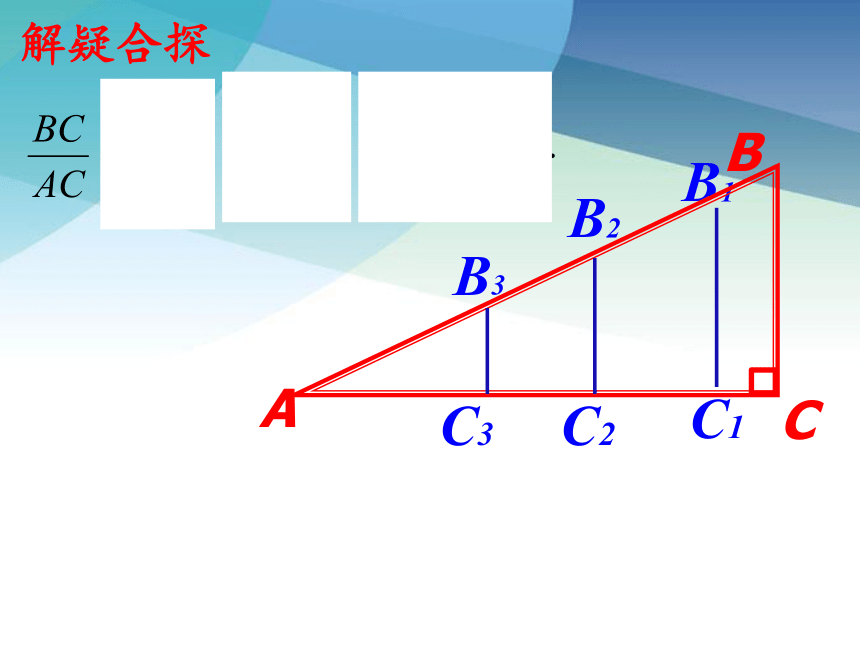
B3
C3
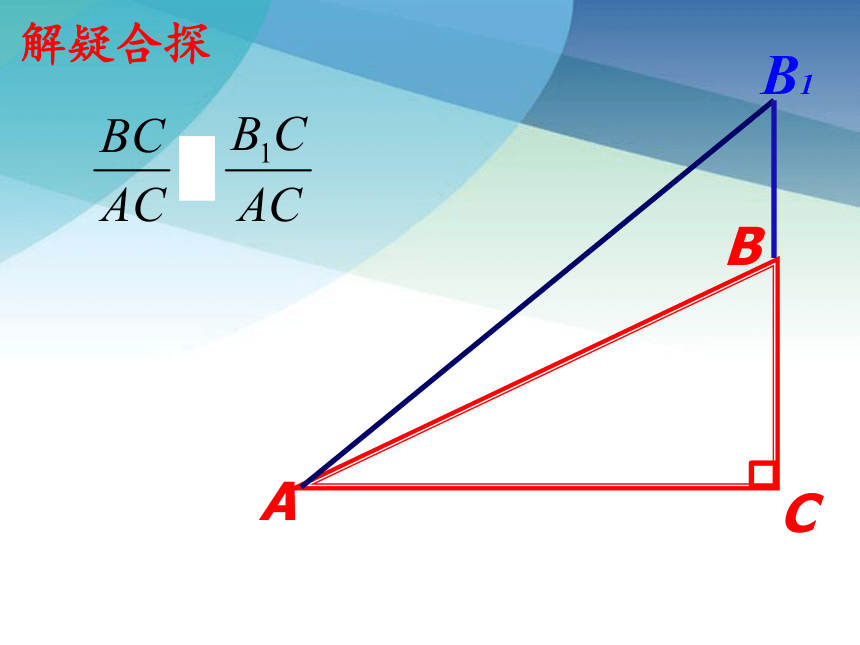
解疑合探
B1
A
B
C
解疑合探
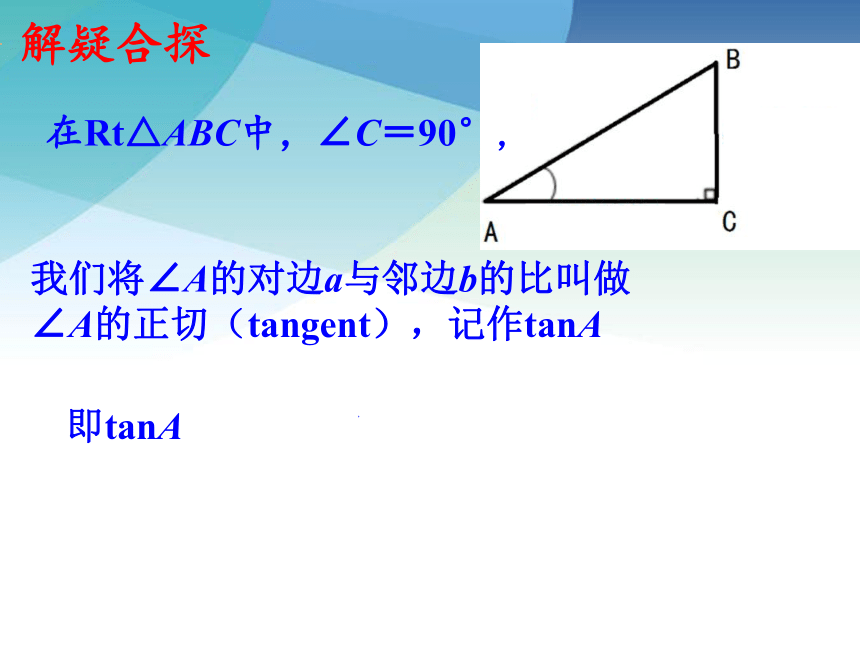
在Rt△ABC中,∠C=90°,
我们将∠A的对边a与邻边b的比叫做∠A的正切(tangent),记作tanA
即tanA= = = .
解疑合探
A
B
C
对边a
邻边b
┌
tanA=
斜边c
1. tanA是在直角三角形中定义的, ∠A是一个锐角;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
A
B
C
对边a
邻边b
┌
tanA=
斜边c
你能写出tanB吗?
1. tanA是在直角三角形中定义的, ∠A是一个锐角;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
∠B的邻边a
∠B的对边b
判断真假:
A
B
C
(1)
C
┍
A
B
7m
10m
(2)
3.如图 (2)
( ).
2.如图 (2)
( ).
1. 如图 (1)
( ).
错
错
对
质疑共探
A
B
C
∠B对边a
∠A邻边b
┌
tanA=
斜边c
1. ∠A是一个锐角,tanA是在直角三角形中定义的;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
3. tanA是一个比值,无单位;
4.正切揭示了直角三角形中边与角的关系
例1 如图,在Rt△ABC中,∠C=90°,AC=8,
AB=10,求tanA、tanB.
质疑共探
D
变式:
在Rt△ABC中,∠C=90°,AB=10,tanA=
你能求出哪些量呢?
1 如图,在Rt△ABC中,锐角A的邻边和斜边
同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
质疑共探
如图(2),等边三角形ABC中,AB=AC=BC
2 如图(1),在Rt△ABC中,AB=AC
质疑共探
你能用今天所学的知识求出哪些角的正切值?
⑴
⑵
B1
A
B
C
解疑合探
<
tan∠BAC
tan∠B1AC
<
颗粒归仓
回顾所学,我想说…
悬疑再探
颗粒归仓
悬疑再探
1 学习了一个重要概念
3 体会并感受了重要的数学思想
函数思想
数形结合思想
方程思想
转化思想
2 探究了几个重要结论
从特殊到一般思想
直角三角形
两锐角关系
三边关系
三角形的
内角和
勾股定理
边角关系
悬疑再探
锐角三
角函数
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角正切函数关系,来对山川地势进行测量并作计算.
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成的, 16世纪,德国数学家雷提库斯把锐角三角函数定义为直角三角形的边长之比,并采用了六个函数(正切、正弦、余弦、余切、正割、余割)。三角函数在建筑,航海及天文等方面测量、计算中有着重要的作用.
悬疑再探
你能沿着本节探究学习正切函数的基本思路和经验,去尝试发现直角三角形的边角关系的其它类型的函数吗?
7.1 正切
A
C
B
D
设疑自探
设疑自探
A
C
B
D
更陡!
8米
12米
6米
6米
8米
4米
解疑合探
哪个台阶更陡?你是如何判断的?
①
③
②
8
12米
6
6米
8米
4米
①
③
②
解疑合探
哪个台阶更陡?你是如何判断的?
哪个台阶更陡?你是如何判断的?
B1
C1
A
B
C
解疑合探
A1
B2
C2
A
B
C
解疑合探
A2
B1
C1
A
B
C
B2
C2
B3
C3
解疑合探
B1
A
B
C
解疑合探
在Rt△ABC中,∠C=90°,
我们将∠A的对边a与邻边b的比叫做∠A的正切(tangent),记作tanA
即tanA= = = .
解疑合探
A
B
C
对边a
邻边b
┌
tanA=
斜边c
1. tanA是在直角三角形中定义的, ∠A是一个锐角;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
A
B
C
对边a
邻边b
┌
tanA=
斜边c
你能写出tanB吗?
1. tanA是在直角三角形中定义的, ∠A是一个锐角;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
∠B的邻边a
∠B的对边b
判断真假:
A
B
C
(1)
C
┍
A
B
7m
10m
(2)
3.如图 (2)
( ).
2.如图 (2)
( ).
1. 如图 (1)
( ).
错
错
对
质疑共探
A
B
C
∠B对边a
∠A邻边b
┌
tanA=
斜边c
1. ∠A是一个锐角,tanA是在直角三角形中定义的;
友情提示:
解疑合探
2. tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
3. tanA是一个比值,无单位;
4.正切揭示了直角三角形中边与角的关系
例1 如图,在Rt△ABC中,∠C=90°,AC=8,
AB=10,求tanA、tanB.
质疑共探
D
变式:
在Rt△ABC中,∠C=90°,AB=10,tanA=
你能求出哪些量呢?
1 如图,在Rt△ABC中,锐角A的邻边和斜边
同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
质疑共探
如图(2),等边三角形ABC中,AB=AC=BC
2 如图(1),在Rt△ABC中,AB=AC
质疑共探
你能用今天所学的知识求出哪些角的正切值?
⑴
⑵
B1
A
B
C
解疑合探
<
tan∠BAC
tan∠B1AC
<
颗粒归仓
回顾所学,我想说…
悬疑再探
颗粒归仓
悬疑再探
1 学习了一个重要概念
3 体会并感受了重要的数学思想
函数思想
数形结合思想
方程思想
转化思想
2 探究了几个重要结论
从特殊到一般思想
直角三角形
两锐角关系
三边关系
三角形的
内角和
勾股定理
边角关系
悬疑再探
锐角三
角函数
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角正切函数关系,来对山川地势进行测量并作计算.
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成的, 16世纪,德国数学家雷提库斯把锐角三角函数定义为直角三角形的边长之比,并采用了六个函数(正切、正弦、余弦、余切、正割、余割)。三角函数在建筑,航海及天文等方面测量、计算中有着重要的作用.
悬疑再探
你能沿着本节探究学习正切函数的基本思路和经验,去尝试发现直角三角形的边角关系的其它类型的函数吗?
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
