高中数学人教A版2019必修第二册 《复数的加、减运算及其几何意义》名师课件(共34张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 《复数的加、减运算及其几何意义》名师课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 09:44:04 | ||
图片预览








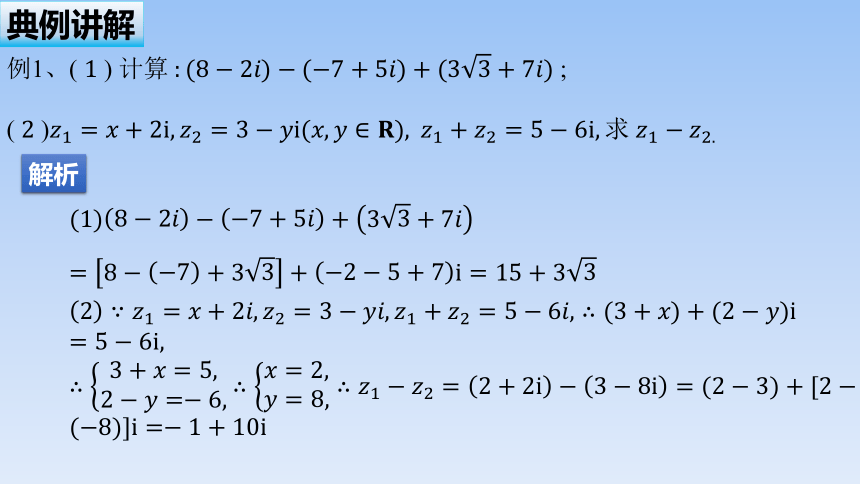


文档简介
(共34张PPT)
复数的几何意义是什么?
复数的几何意义
类比实数的运算法则能否得到复数的运算法则?
(1) 虚数单位i
(2) 复数的分类?
(3) 复数相等的等价条件?
复习引入
人教A版同步教材名师课件
复数的加、减运算及其几何意义
学习目标
学 习 目 标 核心素养
借助多项式加法与减法的运算性质,理解复数加法与减法运算的概念、运算公式与加法运算律 数学运算
借助平面向量的加、减法法则,理解复数加、减法的几何意义 直观想象
学习目标
课程目标:
1.掌握复数代数形式的加、减运算法则;
2.了解复数代数形式的加、减运算的几何意义.
数学学科素养
1.逻辑推理:根据复数与平面向量的对应关系推导其几何意义;
2.数学运算:根据复数加、减运算及有其几何意义求相关问题;
3.数学建模:结合复数加、减运算的几何意义和平面图形,数形结合,综合应用.
1、复数的加法法则:设是任意两复数,那么它们的和:
(1)复数的加法运算法则是一种规定.当时与实数加法法则保持一致
(2)很明显,两个复数的和仍然是一个复数,对于复数的加法可以推广到多个复数相加的情形.
探究新知
设
则
显然:
同理可得:
实数加法运算的交换律、结合律在复数集C中依然成立
复数的加法满足交换律,结合律吗?
复数的加法满足交换律、结合律,即对任意
探究新知
y
x
O
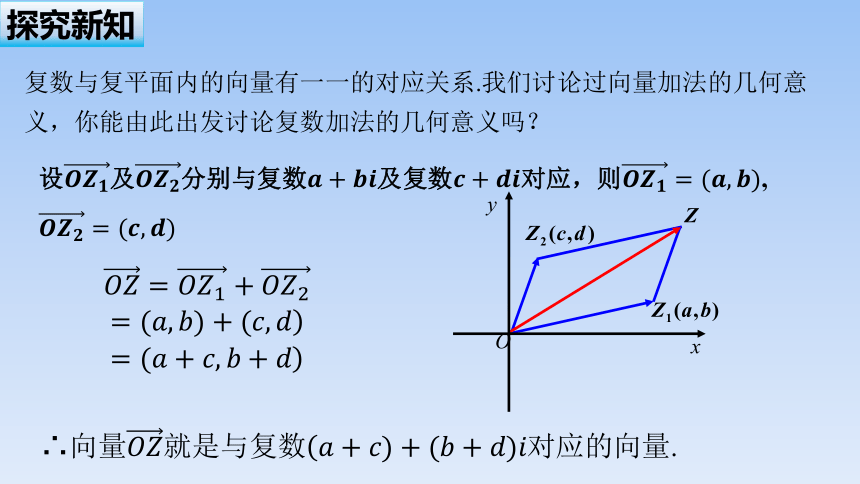
设及分别与复数及复数对应,则,
∴向量就是与复数对应的向量.
复数与复平面内的向量有一一的对应关系.我们讨论过向量加法的几何意义,你能由此出发讨论复数加法的几何意义吗?
探究新知
我们规定,复数的减法是加法的逆运算,即把满足 的复数叫做复数减去复数的差,记作
事实上,由复数相等的定义,有:
由此,得
所以
即:
两个复数相减就是把实部与实部、虚部与虚部分别相减,即
探究新知
类比复数加法的几何意义,请指出复数减法的几何意义?
y
x
O
探究新知
设及分别与复数及复数对应,则,
∴向量就是与复数对应的向量.
典例讲解
解析
例2、(1)计算(3-2i)+(-4i+5)-(6-3i).
(2)若(a+bi)-(2a-3bi)-3i=2+i,求实数a,b.
(1)原式=(3+5-6)+[-2+(-4)-(-3)]i=2-3i.
(2)因为(a+bi)-(2a-3bi)-3i=(a-2a)+[b-(-3b)-3]i=-a+(4b-3)i,
即-a+(4b-3)i=2+i,
典例讲解
解析
复数的加法运算类似于多项式的合并同类项,首先正确确定各个复数的实部、虚部,再将所有实部和虚部分别求和,最后将实部和作为实部,虚部和作为虚部,写出复数的代数形式.注意减法要将减数的实部、虚部变为相反数进行求和.
方法归纳
变式训练
则=_________.
A.-4 B.7 C.-8 D.5
解析
,
由复数相等的充要条件可知
解得.
D
变式训练
2.(1)已知求z1+z2, z1-z2.
(1)z1+z2=2+3+(-1+2)=1+5,
z1-z2=2+3-(-1+2)=3+.
(2) =1+.
(3)原式即为(x-3)+(-2-y)=3y+(2x-1),
所以解得x=0,y=-1.
(2)计算
(3)若求实数.
解析
变式训练
解析
3. 计算
将上述1009个式子左右分别相加,得原式
.
解法二:
,
……
=
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
,
则在复平面内对应的点的坐标为,位于第四象限.
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
,
.
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
对应的点的坐标为.
∵复数z对应的点在第二象限内,
即
方法归纳
(1)先利用加法法则求出,然后根据复数的几何意义确定对应点所在的象限.
(2)根据复数的减法法则以及复数模的定义即可求出.
(3)先求出复数z在复平面内对应点的坐标,再根据题意列不等式(组)求解.
变式训练
4.(1)已知,其中为实数, 为虚数单位,若,则的值为( )
A.4 B.-1 C.6 D.0
(2)设在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(3)复数在复平面内对应的点位于第__________象限.
在复平面内对应的点的坐标为所以复数z在复平面内对应的点在第二象限,故选B.
解析
.
在复平面内对应的点的坐标为位于第二象限.
例4、在复平面内,A,B,C分别对应复数z1=1+i,z2=5+i,z3=3+3i,以AB,AC为邻边作一个平行四边形ABDC,求D点对应的复数z4及AD的长.
如图所示:对应复数z3-z1,对应复数z2-z1,
对应复数z4-z1.由向量的平行四边形法则,
得=+,
所以z4-z1=(z2-z1)+(z3-z1),
所以z4=z2+z3-z1=(5+i)+(3+3i)-(1+i)=7+3i,
所以AD的长为||=|z4-z1|
=|(7+3i)-(1+i)|=|6+2i|=2.
典例讲解
解析
例5、已知复平面内有平行四边形ABCD,O为原点,点A对应的复数为,向量对应的复数为,向量对应的复数为
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
典例讲解
解析
,
,.
, 向量对应的复数为,即.
,
由得 ,∴点D对应的复数为5.
例5、已知复平面内有平行四边形ABCD,O为原点,点A对应的复数为,向量对应的复数为,向量对应的复数为
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
典例讲解
解析
方法归纳
利用向量的加法“首尾相接”和减法“指向被减向量”的特点,在三角形内可求得和、差向量及其对应的复数.注意向量对应的复数是(终点对应的复数减去起点对应的复数).
变式训练
5.在复平面内, ABCD的点A、B对应的复数分别为zA=,zB=,且C、D对应的复数zC 与zD 满足zC-2zD=,求zC与zD.
= ,
如图所示,在 ABCD中,
所以zB-zA=zC-zD,即zC-zD==4,①
又zC-2zD=,②
由①②解得:zC=,zD=.
解析
典例讲解
例6、设求
解析
典例讲解
例6、设求
解析
解法二:易知,
将已知数值代入.
解法三:作出对应的向量,并利用平行四边形法则作.
不共线(若2或0,与题设矛盾),
∴平行四边形为菱形.
,即四边形为正方形,
方法归纳
在解决有关复数模的问题时,应结合复数复数模的几何意义和平面几何等知识,将代数问题转化为几何问题,从而达到优化解题过程的目的.
该结论应牢记,做题时可直接运用.
变式训练
6.已知 求
解析
又∵与轴正半轴的夹角为,∴点A在轴上,即A(1,0).
由于
三点均在以原点为圆心,1为半径的圆上,如图所示,
由平行四边形法则和余弦定理易得
故∠AOC=60°,
∴平行四边形OACB为菱形,且△BOC,△COA都是等边三角形,即
变式训练
6.已知 求
解析
∵
当堂练习
1.若复数满足的虚部是( )
A.-2 B.4 C.-3 D.3
B
D
3.在平行四边形ABCD中,对角线AC与BD相交于点O,若向量对应的复数分别是对应的复数是( )
D
当堂练习
4.在复平面内,对应的复数分别为则对应的复数为( )
A.-1-5i B.-1+5i C.3-4i D.3+4i
A
归纳小结
复数加减法的运算法则
应用
复数加减法的几何意义
平行四边形法则和三角形法则
课本P77练习:1、2、4
作 业
复数的几何意义是什么?
复数的几何意义
类比实数的运算法则能否得到复数的运算法则?
(1) 虚数单位i
(2) 复数的分类?
(3) 复数相等的等价条件?
复习引入
人教A版同步教材名师课件
复数的加、减运算及其几何意义
学习目标
学 习 目 标 核心素养
借助多项式加法与减法的运算性质,理解复数加法与减法运算的概念、运算公式与加法运算律 数学运算
借助平面向量的加、减法法则,理解复数加、减法的几何意义 直观想象
学习目标
课程目标:
1.掌握复数代数形式的加、减运算法则;
2.了解复数代数形式的加、减运算的几何意义.
数学学科素养
1.逻辑推理:根据复数与平面向量的对应关系推导其几何意义;
2.数学运算:根据复数加、减运算及有其几何意义求相关问题;
3.数学建模:结合复数加、减运算的几何意义和平面图形,数形结合,综合应用.
1、复数的加法法则:设是任意两复数,那么它们的和:
(1)复数的加法运算法则是一种规定.当时与实数加法法则保持一致
(2)很明显,两个复数的和仍然是一个复数,对于复数的加法可以推广到多个复数相加的情形.
探究新知
设
则
显然:
同理可得:
实数加法运算的交换律、结合律在复数集C中依然成立
复数的加法满足交换律,结合律吗?
复数的加法满足交换律、结合律,即对任意
探究新知
y
x
O
设及分别与复数及复数对应,则,
∴向量就是与复数对应的向量.
复数与复平面内的向量有一一的对应关系.我们讨论过向量加法的几何意义,你能由此出发讨论复数加法的几何意义吗?
探究新知
我们规定,复数的减法是加法的逆运算,即把满足 的复数叫做复数减去复数的差,记作
事实上,由复数相等的定义,有:
由此,得
所以
即:
两个复数相减就是把实部与实部、虚部与虚部分别相减,即
探究新知
类比复数加法的几何意义,请指出复数减法的几何意义?
y
x
O
探究新知
设及分别与复数及复数对应,则,
∴向量就是与复数对应的向量.
典例讲解
解析
例2、(1)计算(3-2i)+(-4i+5)-(6-3i).
(2)若(a+bi)-(2a-3bi)-3i=2+i,求实数a,b.
(1)原式=(3+5-6)+[-2+(-4)-(-3)]i=2-3i.
(2)因为(a+bi)-(2a-3bi)-3i=(a-2a)+[b-(-3b)-3]i=-a+(4b-3)i,
即-a+(4b-3)i=2+i,
典例讲解
解析
复数的加法运算类似于多项式的合并同类项,首先正确确定各个复数的实部、虚部,再将所有实部和虚部分别求和,最后将实部和作为实部,虚部和作为虚部,写出复数的代数形式.注意减法要将减数的实部、虚部变为相反数进行求和.
方法归纳
变式训练
则=_________.
A.-4 B.7 C.-8 D.5
解析
,
由复数相等的充要条件可知
解得.
D
变式训练
2.(1)已知求z1+z2, z1-z2.
(1)z1+z2=2+3+(-1+2)=1+5,
z1-z2=2+3-(-1+2)=3+.
(2) =1+.
(3)原式即为(x-3)+(-2-y)=3y+(2x-1),
所以解得x=0,y=-1.
(2)计算
(3)若求实数.
解析
变式训练
解析
3. 计算
将上述1009个式子左右分别相加,得原式
.
解法二:
,
……
=
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
,
则在复平面内对应的点的坐标为,位于第四象限.
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
,
.
典例讲解
例3、(1)设在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)若复数z满足=___________.
(3)复平面内,若所对应的点在第二象限内,则实数m的取值范围是___________.
解析
对应的点的坐标为.
∵复数z对应的点在第二象限内,
即
方法归纳
(1)先利用加法法则求出,然后根据复数的几何意义确定对应点所在的象限.
(2)根据复数的减法法则以及复数模的定义即可求出.
(3)先求出复数z在复平面内对应点的坐标,再根据题意列不等式(组)求解.
变式训练
4.(1)已知,其中为实数, 为虚数单位,若,则的值为( )
A.4 B.-1 C.6 D.0
(2)设在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(3)复数在复平面内对应的点位于第__________象限.
在复平面内对应的点的坐标为所以复数z在复平面内对应的点在第二象限,故选B.
解析
.
在复平面内对应的点的坐标为位于第二象限.
例4、在复平面内,A,B,C分别对应复数z1=1+i,z2=5+i,z3=3+3i,以AB,AC为邻边作一个平行四边形ABDC,求D点对应的复数z4及AD的长.
如图所示:对应复数z3-z1,对应复数z2-z1,
对应复数z4-z1.由向量的平行四边形法则,
得=+,
所以z4-z1=(z2-z1)+(z3-z1),
所以z4=z2+z3-z1=(5+i)+(3+3i)-(1+i)=7+3i,
所以AD的长为||=|z4-z1|
=|(7+3i)-(1+i)|=|6+2i|=2.
典例讲解
解析
例5、已知复平面内有平行四边形ABCD,O为原点,点A对应的复数为,向量对应的复数为,向量对应的复数为
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
典例讲解
解析
,
,.
, 向量对应的复数为,即.
,
由得 ,∴点D对应的复数为5.
例5、已知复平面内有平行四边形ABCD,O为原点,点A对应的复数为,向量对应的复数为,向量对应的复数为
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
典例讲解
解析
方法归纳
利用向量的加法“首尾相接”和减法“指向被减向量”的特点,在三角形内可求得和、差向量及其对应的复数.注意向量对应的复数是(终点对应的复数减去起点对应的复数).
变式训练
5.在复平面内, ABCD的点A、B对应的复数分别为zA=,zB=,且C、D对应的复数zC 与zD 满足zC-2zD=,求zC与zD.
= ,
如图所示,在 ABCD中,
所以zB-zA=zC-zD,即zC-zD==4,①
又zC-2zD=,②
由①②解得:zC=,zD=.
解析
典例讲解
例6、设求
解析
典例讲解
例6、设求
解析
解法二:易知,
将已知数值代入.
解法三:作出对应的向量,并利用平行四边形法则作.
不共线(若2或0,与题设矛盾),
∴平行四边形为菱形.
,即四边形为正方形,
方法归纳
在解决有关复数模的问题时,应结合复数复数模的几何意义和平面几何等知识,将代数问题转化为几何问题,从而达到优化解题过程的目的.
该结论应牢记,做题时可直接运用.
变式训练
6.已知 求
解析
又∵与轴正半轴的夹角为,∴点A在轴上,即A(1,0).
由于
三点均在以原点为圆心,1为半径的圆上,如图所示,
由平行四边形法则和余弦定理易得
故∠AOC=60°,
∴平行四边形OACB为菱形,且△BOC,△COA都是等边三角形,即
变式训练
6.已知 求
解析
∵
当堂练习
1.若复数满足的虚部是( )
A.-2 B.4 C.-3 D.3
B
D
3.在平行四边形ABCD中,对角线AC与BD相交于点O,若向量对应的复数分别是对应的复数是( )
D
当堂练习
4.在复平面内,对应的复数分别为则对应的复数为( )
A.-1-5i B.-1+5i C.3-4i D.3+4i
A
归纳小结
复数加减法的运算法则
应用
复数加减法的几何意义
平行四边形法则和三角形法则
课本P77练习:1、2、4
作 业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
