华师大版 2022七年级数学上册1.2 人人都能学会数学 授课课件共41张PPT)
文档属性
| 名称 | 华师大版 2022七年级数学上册1.2 人人都能学会数学 授课课件共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 904.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 21:49:55 | ||
图片预览










文档简介
(共41张PPT)
第1章 走进数学世界
第2课时 人人都能学会数学
第1章 走进数学世界
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
从生活中感知数学
从数图中认识数学
课时导入
复习提问
引出问题
华罗庚的故事
宇宙之大,粒子之微,火箭之速,
化工之巧,地球之 变,生物之谜,日
用之繁,无处不用数学.
——华罗庚
我国著名的数学家华罗庚说:“聪明在于学习,天
才由于积累.”这句话正是他一生的真实写照.
课时导入
华罗庚,1910年出生于江苏省金坛县,1924年毕业于该县公立初级中学.以后,他又到上海中华职业学校读书,用不到一年半的时间,就读完了两年的课程.15岁的时候,华罗庚迫于家境困难而辍学.返回家乡后,他一面帮助父亲在小杂货店里干活、记账,一面钻研数学.
课时导入
父亲不愿意让他读书,而是让他干活.就是在这种生活艰难、无人指导的困境下,在一间斗室里,他以昏暗的油灯为伴,孜孜不倦地坚持自学.20岁时,他的一篇论文《苏家驹之代数的五次方程式解法不能成立之理由》发表在上海《科学》杂志上,显示出了这位20岁青年的数学才华.然而就在同一年,华罗庚患了严重的伤寒病和关节炎.在与疾病的斗争中,他
课时导入
意志顽强,坚韧不拔,终于战胜了病魔,但他的左腿瘸了.就是在此期间,他仍然努力钻研数学,接连取得了许多重大的科研成果.一般人从初中到大学毕业要八年时间,而华罗庚完全依靠自学,只用了六年半的时间.华罗庚正是凭着这种刻苦钻研的精神,终于成为举世公认的大数学家.
知识点
从生活中感知数学
知1-导
感悟新知
1
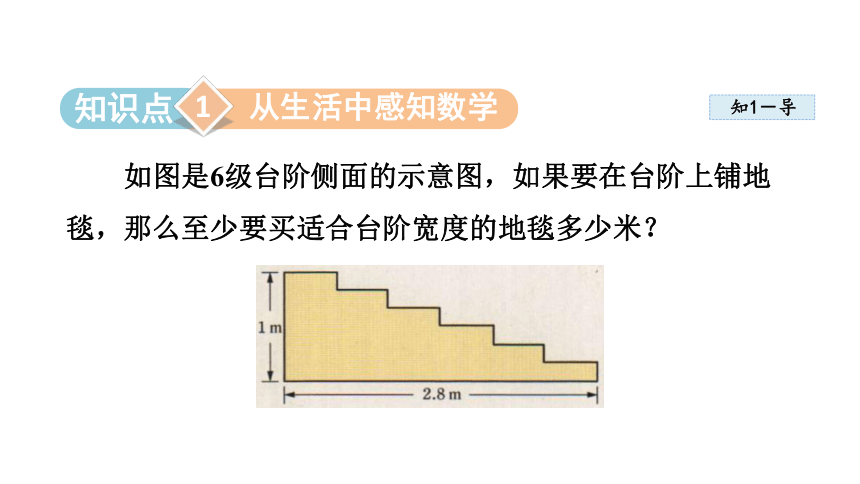
如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,那么至少要买适合台阶宽度的地毯多少米?
知1-导
感悟新知
要在台阶上铺地毯,实际上并不需要测出每一级台阶的长度.我们把上页图想象为由一根绳子围成的图形,将它拉成为一个长和宽分别为2. 8米和1米的长方形. 因此,台阶的总长就是
2.8 + 1 = 3.8 (米),
也就是至少要买适合台阶宽度的地毯3. 8米.
知1-讲
感悟新知
数学并不神秘,不只是天才才能学会数学,只要我们刻苦努力,对数学感兴趣,人人都能学会数学,相信你通过阅读课本中的材料一定可以从中受到启发.只要对数学有浓厚的兴趣,善于发现问题和提出问题,善于独立思考问题,再加上持之以恒的学习态度,相信每一位同学都能学会数学.
知1-练
感悟新知
例 1
猜谜语是人们最喜爱的一项有益思维训练的活动,利用数或算式制作谜语更具有特色,根据下面的数或算式各猜一个成语.
(1) (2)0000;(3)1 0002=100×100×100;
(4)1 510;(5)3 322.
解:(1)七上八下.(2)万无一失.(3)千方百计.
(4)一五一十.(5)三三两两.
猜数学谜语主要是提高学生学习数学的兴趣,增强数学趣味性.
知1-练
感悟新知
导引:寻找数的分布情况或数据中缺少的数,找到规律以后就可以写出符合规律的成语.
知1-练
感悟新知
五一期间,小明和爸爸、妈妈三人来到西安参观某生态园,该园的面积约有800 000 m2,若按比例尺 1∶
2 000缩小后,其面积大约相当于( )
A.一个篮球场的面积
B.一张乒乓球台台面的面积
C.《陕西日报》一个版面的面积
D.《数学》课本封面的面积
C
例2
知1-练
感悟新知
解:先求出该园按比例尺1∶2 000缩小后的面积:
800 000÷2 0002=0.2(m2),然后看给出的四个选项,显然A和B都不止0.2 m2,《数学》课本封面又不够0.2 m2.
误区警示 :
在生活中,估计问题时,最容易犯的错误就是凭直觉去猜测,正确的方法是凭相关的数据进行分析.
知1-练
感悟新知
观察下列等式:
31=3,32=9,33=27,34=81,35=243, 36=729,
37=2 187…… 则3+32+33+34+…+32 019 的末尾数
字是( )
A.3 B.2 C.9 D.0
C
例 3
知1-练
感悟新知
解:观察31=3,32=9,33=27,34=81,35=243,36=729,37=2 187……知它们的末尾数字规律是3,9,7,1四个数字为一个循环, 再观察3+9+7+1+3+9+7+1+3+9+7+1+…的末尾数字规律为3,2,9,0 四个数字为一个循环,2 019÷4=504……3,故3+32+33+34+…+32 019 的末尾数字是9.
知1-练
感悟新知
方法规律:
1.观察规律的三种主要途径:
(1)从数的特征观察;
(2)从图形的结构观察;
(3) 通过对简单、特殊情况的观察,再推广到一般情况.
2.规律探究的基本原则:
(1)遵循类推原则,项找项的规律,和找和的规律,差找差的规律,积找积的规律;
(2)遵循有序原则,从特殊开始或从简单开始,发现规律,再验证运用规律.
知1-练
感悟新知
在平静的湖水中,一艘快艇的最高速度是20米/秒,一艘气垫船也以20米/秒的速度和它并排前进.气垫船说:“快艇兄弟,我们就用这样的速度到那条流速为4米/秒的河中去比赛,先顺流而下1 000米,再逆流回到起点,看谁先完成.”请你算一算(掉头时间不计),比赛的结果怎样?若河水的流速为10米/秒,结果又怎样?若河水的流速为20米/秒呢?(假设水流对气垫船的速度没有影响)
例4
知1-练
感悟新知
解:由于水流对气垫船的速度没有影响,
所以气垫船所用时间为
快艇顺流所用时间为
逆流所用时间为
总时间约为41.7+62.5=104.2(秒).
100<104.2,故气垫船先到.
知1-练
感悟新知
若水流速度为10米/秒,则快艇所用总时间为
若水流速度为20米/秒,则快艇逆流速度为0米/秒,
不能完成比赛.
故水流速度为10米/秒时气垫船先到,水流速度为
20米/秒时不能完成比赛.
1.小说《达·芬奇密码》中的一个故事里出现了一
串神秘的数,将这串神秘的数按从小到大的顺序
排列为:1,1,2,3,5,8,…,则这串数的第
9个数是( )
A.13 B.21 C.34 D.55
知1-练
感悟新知
2.要从一张长为40厘米,宽为20厘米的长方形纸片
中,剪出长为18厘米,宽为12厘米的长方形纸片,
最多能剪出( )
A.1张 B.2张 C.3张 D.4张
知1-练
感悟新知
3.如图,有两个完全重合的长方形,将其中一个始终保持不动,另一个长方形绕其中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是( )
A.图① B.图②
C.图③ D.图④
知1-练
感悟新知
4.如图,将一张正方形纸片沿对角线折叠一次,然后在得到的三角形三个角上各挖去一个圆洞,将正方形纸片展开,得到的图案是( )
知1-练
感悟新知
知2-导
感悟新知
知识点
从数图中认识数学
2
去掉一个最高分和一个最低分
在歌手电视大奖赛上,全部评委亮分之后,在计算平均分时,往往要先去掉一个最高分和一个最低分.你知道这是为什么吗?
大奖赛上,去掉一个最高分和一个最低分的目的,
是要略去评委评分中可能出现的异常值,使得一个或两个评委的个人意愿不致影响参赛歌手的总成绩.
知2-导
感悟新知
我们不妨看一个极端的例子.某大奖赛有7名评委,
他们给甲乙两选手打的分数分别是:
甲:9. 55, 9.55, 9.55, 9.55, 9. 55, 9.60, 9.90;
乙:9. 50, 9.60, 9.60, 9.60, 9.60, 9.60, 9.70.
凭直觉,你认为哪个选手比较好一点?
我们用两种方式来计算一下.
(1)直接算7个分数的平均数.
甲的平均分:(9.55×5 + 9.60 +9.90) ÷7 = 9.607;
乙的平均分:(9. 50 + 9. 60×5 +9. 70) ÷7 = 9. 60.
知2-导
感悟新知
(2)去掉一个最高分和一个最低分,计算剩下5个分数的平均数.
甲的平均分:(9.55×4 +9.60)÷ 5 = 9.56;
乙的平均分:(9.60×5)÷ 5 = 9.60.
显然,用第二种方式比较符合直觉(乙比较好一些).
由于评委给甲打分时出现极端的最高分(9. 90),所以直
接计算7个分数的平均数会出现偏差,而采用“去掉一
个最高分和一个最低分”就可避免这样的偏差,显得较
为公平.
知2-练
感悟新知
如图所示,四边形ABCG和四边形CFED是两个相同的平行四边形,AB=BC=CG=GA=1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿平行四边形的边循环运动,行走2 016厘米后停下,则这只蚂蚁停在________点.
例 5
A
知2-讲
感悟新知
总 结
由题意可知蚂蚁由A点开始按ABCDEFCGA的顺序走一圈的路程为8×1=8(厘米),因为2 016÷8=252,所以蚂蚁停在A点.
知2-练
感悟新知
生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数(如图),正方形的方框内的四个数的和是32,那么第一个数是________.
4
例6
知2-练
感悟新知
(2)玛丽也在上面的日历上圈出2×2个数(如图1),斜内的四个数的和是42,则它们分别___________.
(3)莉莉也在日历上圈出5个数(如图2),呈十字框形,它们的和是50,则中间的数是________.
图2
图1
7,8,13,14
10
知2-练
感悟新知
(4)某月有5个星期日的和是75,则这个月中最后一个
星期日是________号;
(5)若干个偶数按每行8个数排成下图:
29
知2-练
感悟新知
①图中方框内的9个数的和与中间的数有什么关系;
②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是________;
③托马斯也画了一个斜框,斜框内9个数的和为270,则斜框的中间一个数是________.
40
30
解:和是中间的数的9倍.
知2-讲
感悟新知
总 结
(1)设第一个数是x,其他的数为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,解得x=4;
(2)设第一个数是x,其他的数为x+1,x+6,x+7,
则x+x+1+x+6+x+7=42,解得x=7.x+1=
8,x+6=13,x+7=14;
(3)设中间的数是x,则5x=50,解得x =10;
知2-讲
感悟新知
总 结
(4)设最后一个星期日是x,则x+x-7+x-14+x-
21+x-28=75,解得x=29;
(5)①和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,设中间
的数是x,则9x=360,解得x=40.
③设中间的数是x,则9x=270,解得x=30.
知2-练
感悟新知
在用黑色围棋进行摆放图案的游戏中,小雨同学摆放了如图所示的各图案,请根据图中的信息完成下列问题.
例 7
知2-练
感悟新知
(1)填写下表:
(2)第50个图案中有________颗围棋;
(3)小雨同学如果继续摆放下去,那么第n个图案就要用____________颗围棋;
3
图案编号 ① ② ③ …
图案中棋子的总数 3 …
10
1 326
知2-练
感悟新知
(4)如果小雨同学手上刚好有90颗围棋,那么他按照这种规律从第1个图案摆放下去,是否可以摆放成完整的图案后刚好90颗围棋一颗不剩?如果可以,那么刚好摆放完成几个完整的图案?如果不可以,那么最多可以摆放多少个完整的图案?还剩下几颗围棋?(只答结果,不说明理由)
解:不可以,最多可以摆放6个完整的图案,还剩下7颗围棋.
1.小王同学利用计算机设计了一个计算程序,输入和输出的数据如下表:
当输入的数据是8时,输出的数据是( )
A. B. C. D.
知2-练
感悟新知
输入 1 2 3 4 5 …
输出 …
知2-练
感悟新知
2. (2015·广安)在市委、市政府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城 市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明
C.城 D.国
知2-练
感悟新知
3.观察图中图形的构成规律,根据此规律,第8个图形中有________个圆.
课堂小结
人人都能学会数学
解决操作性问题一般有两种思路:
一种是结合操作过程展开空间想象,这种方法有利
于培养我们的空间想象能力,提高我们的思维能力;另
一种是通过动手操作来解答,这种方法正确率高,有利
于培养我们的动手操作能力.
第1章 走进数学世界
第2课时 人人都能学会数学
第1章 走进数学世界
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
从生活中感知数学
从数图中认识数学
课时导入
复习提问
引出问题
华罗庚的故事
宇宙之大,粒子之微,火箭之速,
化工之巧,地球之 变,生物之谜,日
用之繁,无处不用数学.
——华罗庚
我国著名的数学家华罗庚说:“聪明在于学习,天
才由于积累.”这句话正是他一生的真实写照.
课时导入
华罗庚,1910年出生于江苏省金坛县,1924年毕业于该县公立初级中学.以后,他又到上海中华职业学校读书,用不到一年半的时间,就读完了两年的课程.15岁的时候,华罗庚迫于家境困难而辍学.返回家乡后,他一面帮助父亲在小杂货店里干活、记账,一面钻研数学.
课时导入
父亲不愿意让他读书,而是让他干活.就是在这种生活艰难、无人指导的困境下,在一间斗室里,他以昏暗的油灯为伴,孜孜不倦地坚持自学.20岁时,他的一篇论文《苏家驹之代数的五次方程式解法不能成立之理由》发表在上海《科学》杂志上,显示出了这位20岁青年的数学才华.然而就在同一年,华罗庚患了严重的伤寒病和关节炎.在与疾病的斗争中,他
课时导入
意志顽强,坚韧不拔,终于战胜了病魔,但他的左腿瘸了.就是在此期间,他仍然努力钻研数学,接连取得了许多重大的科研成果.一般人从初中到大学毕业要八年时间,而华罗庚完全依靠自学,只用了六年半的时间.华罗庚正是凭着这种刻苦钻研的精神,终于成为举世公认的大数学家.
知识点
从生活中感知数学
知1-导
感悟新知
1
如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,那么至少要买适合台阶宽度的地毯多少米?
知1-导
感悟新知
要在台阶上铺地毯,实际上并不需要测出每一级台阶的长度.我们把上页图想象为由一根绳子围成的图形,将它拉成为一个长和宽分别为2. 8米和1米的长方形. 因此,台阶的总长就是
2.8 + 1 = 3.8 (米),
也就是至少要买适合台阶宽度的地毯3. 8米.
知1-讲
感悟新知
数学并不神秘,不只是天才才能学会数学,只要我们刻苦努力,对数学感兴趣,人人都能学会数学,相信你通过阅读课本中的材料一定可以从中受到启发.只要对数学有浓厚的兴趣,善于发现问题和提出问题,善于独立思考问题,再加上持之以恒的学习态度,相信每一位同学都能学会数学.
知1-练
感悟新知
例 1
猜谜语是人们最喜爱的一项有益思维训练的活动,利用数或算式制作谜语更具有特色,根据下面的数或算式各猜一个成语.
(1) (2)0000;(3)1 0002=100×100×100;
(4)1 510;(5)3 322.
解:(1)七上八下.(2)万无一失.(3)千方百计.
(4)一五一十.(5)三三两两.
猜数学谜语主要是提高学生学习数学的兴趣,增强数学趣味性.
知1-练
感悟新知
导引:寻找数的分布情况或数据中缺少的数,找到规律以后就可以写出符合规律的成语.
知1-练
感悟新知
五一期间,小明和爸爸、妈妈三人来到西安参观某生态园,该园的面积约有800 000 m2,若按比例尺 1∶
2 000缩小后,其面积大约相当于( )
A.一个篮球场的面积
B.一张乒乓球台台面的面积
C.《陕西日报》一个版面的面积
D.《数学》课本封面的面积
C
例2
知1-练
感悟新知
解:先求出该园按比例尺1∶2 000缩小后的面积:
800 000÷2 0002=0.2(m2),然后看给出的四个选项,显然A和B都不止0.2 m2,《数学》课本封面又不够0.2 m2.
误区警示 :
在生活中,估计问题时,最容易犯的错误就是凭直觉去猜测,正确的方法是凭相关的数据进行分析.
知1-练
感悟新知
观察下列等式:
31=3,32=9,33=27,34=81,35=243, 36=729,
37=2 187…… 则3+32+33+34+…+32 019 的末尾数
字是( )
A.3 B.2 C.9 D.0
C
例 3
知1-练
感悟新知
解:观察31=3,32=9,33=27,34=81,35=243,36=729,37=2 187……知它们的末尾数字规律是3,9,7,1四个数字为一个循环, 再观察3+9+7+1+3+9+7+1+3+9+7+1+…的末尾数字规律为3,2,9,0 四个数字为一个循环,2 019÷4=504……3,故3+32+33+34+…+32 019 的末尾数字是9.
知1-练
感悟新知
方法规律:
1.观察规律的三种主要途径:
(1)从数的特征观察;
(2)从图形的结构观察;
(3) 通过对简单、特殊情况的观察,再推广到一般情况.
2.规律探究的基本原则:
(1)遵循类推原则,项找项的规律,和找和的规律,差找差的规律,积找积的规律;
(2)遵循有序原则,从特殊开始或从简单开始,发现规律,再验证运用规律.
知1-练
感悟新知
在平静的湖水中,一艘快艇的最高速度是20米/秒,一艘气垫船也以20米/秒的速度和它并排前进.气垫船说:“快艇兄弟,我们就用这样的速度到那条流速为4米/秒的河中去比赛,先顺流而下1 000米,再逆流回到起点,看谁先完成.”请你算一算(掉头时间不计),比赛的结果怎样?若河水的流速为10米/秒,结果又怎样?若河水的流速为20米/秒呢?(假设水流对气垫船的速度没有影响)
例4
知1-练
感悟新知
解:由于水流对气垫船的速度没有影响,
所以气垫船所用时间为
快艇顺流所用时间为
逆流所用时间为
总时间约为41.7+62.5=104.2(秒).
100<104.2,故气垫船先到.
知1-练
感悟新知
若水流速度为10米/秒,则快艇所用总时间为
若水流速度为20米/秒,则快艇逆流速度为0米/秒,
不能完成比赛.
故水流速度为10米/秒时气垫船先到,水流速度为
20米/秒时不能完成比赛.
1.小说《达·芬奇密码》中的一个故事里出现了一
串神秘的数,将这串神秘的数按从小到大的顺序
排列为:1,1,2,3,5,8,…,则这串数的第
9个数是( )
A.13 B.21 C.34 D.55
知1-练
感悟新知
2.要从一张长为40厘米,宽为20厘米的长方形纸片
中,剪出长为18厘米,宽为12厘米的长方形纸片,
最多能剪出( )
A.1张 B.2张 C.3张 D.4张
知1-练
感悟新知
3.如图,有两个完全重合的长方形,将其中一个始终保持不动,另一个长方形绕其中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是( )
A.图① B.图②
C.图③ D.图④
知1-练
感悟新知
4.如图,将一张正方形纸片沿对角线折叠一次,然后在得到的三角形三个角上各挖去一个圆洞,将正方形纸片展开,得到的图案是( )
知1-练
感悟新知
知2-导
感悟新知
知识点
从数图中认识数学
2
去掉一个最高分和一个最低分
在歌手电视大奖赛上,全部评委亮分之后,在计算平均分时,往往要先去掉一个最高分和一个最低分.你知道这是为什么吗?
大奖赛上,去掉一个最高分和一个最低分的目的,
是要略去评委评分中可能出现的异常值,使得一个或两个评委的个人意愿不致影响参赛歌手的总成绩.
知2-导
感悟新知
我们不妨看一个极端的例子.某大奖赛有7名评委,
他们给甲乙两选手打的分数分别是:
甲:9. 55, 9.55, 9.55, 9.55, 9. 55, 9.60, 9.90;
乙:9. 50, 9.60, 9.60, 9.60, 9.60, 9.60, 9.70.
凭直觉,你认为哪个选手比较好一点?
我们用两种方式来计算一下.
(1)直接算7个分数的平均数.
甲的平均分:(9.55×5 + 9.60 +9.90) ÷7 = 9.607;
乙的平均分:(9. 50 + 9. 60×5 +9. 70) ÷7 = 9. 60.
知2-导
感悟新知
(2)去掉一个最高分和一个最低分,计算剩下5个分数的平均数.
甲的平均分:(9.55×4 +9.60)÷ 5 = 9.56;
乙的平均分:(9.60×5)÷ 5 = 9.60.
显然,用第二种方式比较符合直觉(乙比较好一些).
由于评委给甲打分时出现极端的最高分(9. 90),所以直
接计算7个分数的平均数会出现偏差,而采用“去掉一
个最高分和一个最低分”就可避免这样的偏差,显得较
为公平.
知2-练
感悟新知
如图所示,四边形ABCG和四边形CFED是两个相同的平行四边形,AB=BC=CG=GA=1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿平行四边形的边循环运动,行走2 016厘米后停下,则这只蚂蚁停在________点.
例 5
A
知2-讲
感悟新知
总 结
由题意可知蚂蚁由A点开始按ABCDEFCGA的顺序走一圈的路程为8×1=8(厘米),因为2 016÷8=252,所以蚂蚁停在A点.
知2-练
感悟新知
生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数(如图),正方形的方框内的四个数的和是32,那么第一个数是________.
4
例6
知2-练
感悟新知
(2)玛丽也在上面的日历上圈出2×2个数(如图1),斜内的四个数的和是42,则它们分别___________.
(3)莉莉也在日历上圈出5个数(如图2),呈十字框形,它们的和是50,则中间的数是________.
图2
图1
7,8,13,14
10
知2-练
感悟新知
(4)某月有5个星期日的和是75,则这个月中最后一个
星期日是________号;
(5)若干个偶数按每行8个数排成下图:
29
知2-练
感悟新知
①图中方框内的9个数的和与中间的数有什么关系;
②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是________;
③托马斯也画了一个斜框,斜框内9个数的和为270,则斜框的中间一个数是________.
40
30
解:和是中间的数的9倍.
知2-讲
感悟新知
总 结
(1)设第一个数是x,其他的数为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,解得x=4;
(2)设第一个数是x,其他的数为x+1,x+6,x+7,
则x+x+1+x+6+x+7=42,解得x=7.x+1=
8,x+6=13,x+7=14;
(3)设中间的数是x,则5x=50,解得x =10;
知2-讲
感悟新知
总 结
(4)设最后一个星期日是x,则x+x-7+x-14+x-
21+x-28=75,解得x=29;
(5)①和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,设中间
的数是x,则9x=360,解得x=40.
③设中间的数是x,则9x=270,解得x=30.
知2-练
感悟新知
在用黑色围棋进行摆放图案的游戏中,小雨同学摆放了如图所示的各图案,请根据图中的信息完成下列问题.
例 7
知2-练
感悟新知
(1)填写下表:
(2)第50个图案中有________颗围棋;
(3)小雨同学如果继续摆放下去,那么第n个图案就要用____________颗围棋;
3
图案编号 ① ② ③ …
图案中棋子的总数 3 …
10
1 326
知2-练
感悟新知
(4)如果小雨同学手上刚好有90颗围棋,那么他按照这种规律从第1个图案摆放下去,是否可以摆放成完整的图案后刚好90颗围棋一颗不剩?如果可以,那么刚好摆放完成几个完整的图案?如果不可以,那么最多可以摆放多少个完整的图案?还剩下几颗围棋?(只答结果,不说明理由)
解:不可以,最多可以摆放6个完整的图案,还剩下7颗围棋.
1.小王同学利用计算机设计了一个计算程序,输入和输出的数据如下表:
当输入的数据是8时,输出的数据是( )
A. B. C. D.
知2-练
感悟新知
输入 1 2 3 4 5 …
输出 …
知2-练
感悟新知
2. (2015·广安)在市委、市政府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城 市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明
C.城 D.国
知2-练
感悟新知
3.观察图中图形的构成规律,根据此规律,第8个图形中有________个圆.
课堂小结
人人都能学会数学
解决操作性问题一般有两种思路:
一种是结合操作过程展开空间想象,这种方法有利
于培养我们的空间想象能力,提高我们的思维能力;另
一种是通过动手操作来解答,这种方法正确率高,有利
于培养我们的动手操作能力.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
