2021-2022学年山西省各地华东师大版数学八年级上册第十三章 全等三角形 期末试题选编(含解析)
文档属性
| 名称 | 2021-2022学年山西省各地华东师大版数学八年级上册第十三章 全等三角形 期末试题选编(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 792.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览



文档简介
第十三章 全等三角形
一、单选题
1.(2022·山西临汾·八年级期末)三角形中,到三边距离相等的点是( )
A.三条高线所在直线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边的垂直平分线的交点
2.(2022·山西晋中·八年级期末)木工师傅将一个含45度角的三角尺和一个重锤如图放置,就能检查一根横梁是否水平,能解释这一现象的数学知识是( )
A.垂线段最短 B.等腰三角形的“三线合一”
C.角平分线的性质定理 D.线段垂直平分线的性质定理
3.(2022·山西晋中·八年级期末)如图,△ABC中,边AC,AB的垂直平分线相交于点D,若,,则的大小是( )
A.28° B.30° C.32° D.60°
4.(2022·山西运城·八年级期末)如图,在中,,BD平分交AC于点D.若,则的大小为( )
A.66° B.70° C.72° D.75°
5.(2022·山西吕梁·八年级期末)若等腰三角形一腰上的中垂线与另一腰所在直线相交,且交角为50°,则它的底角为( )
A.50° B.70° C.80° D.20°或70°
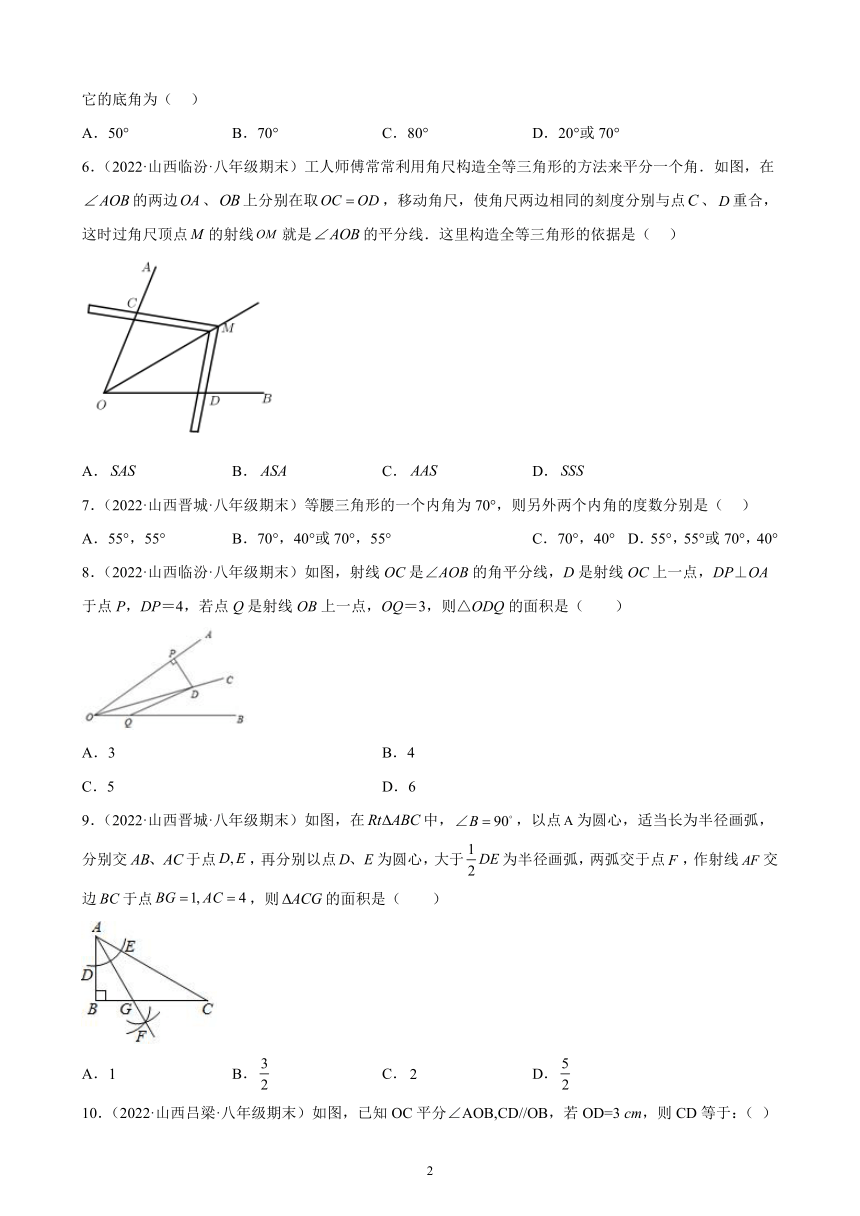
6.(2022·山西临汾·八年级期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.这里构造全等三角形的依据是( )
A. B. C. D.
7.(2022·山西晋城·八年级期末)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55° C.70°,40° D.55°,55°或70°,40°
8.(2022·山西临汾·八年级期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3 B.4
C.5 D.6
9.(2022·山西晋城·八年级期末)如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A. B. C. D.
10.(2022·山西吕梁·八年级期末)如图,已知OC平分∠AOB,CD//OB,若OD=3 cm,则CD等于:( )
A.1.5cm B.2cm C.3cm D.4cm
二、填空题
11.(2022·山西·运城市盐湖区教育科技局教学研究室八年级期末)如图,在中,AD是的角平分线,于E,F、G分别是边AB、AC上的点,连接DF、DG,且,和的面积分别为50和15,则的面积为________.
12.(2022·山西晋城·八年级期末)如图,在中,是边上的中线,E是边上一点,过点C作交的延长线于点F,当,,时,的长是____________.
13.(2022·山西晋中·八年级期末)如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则______度.
14.(2022·山西临汾·八年级期末)如图,点E,F在BC上,BE=CF,∠A=∠D.请添加一个条件________________,使△ABF≌△DCE
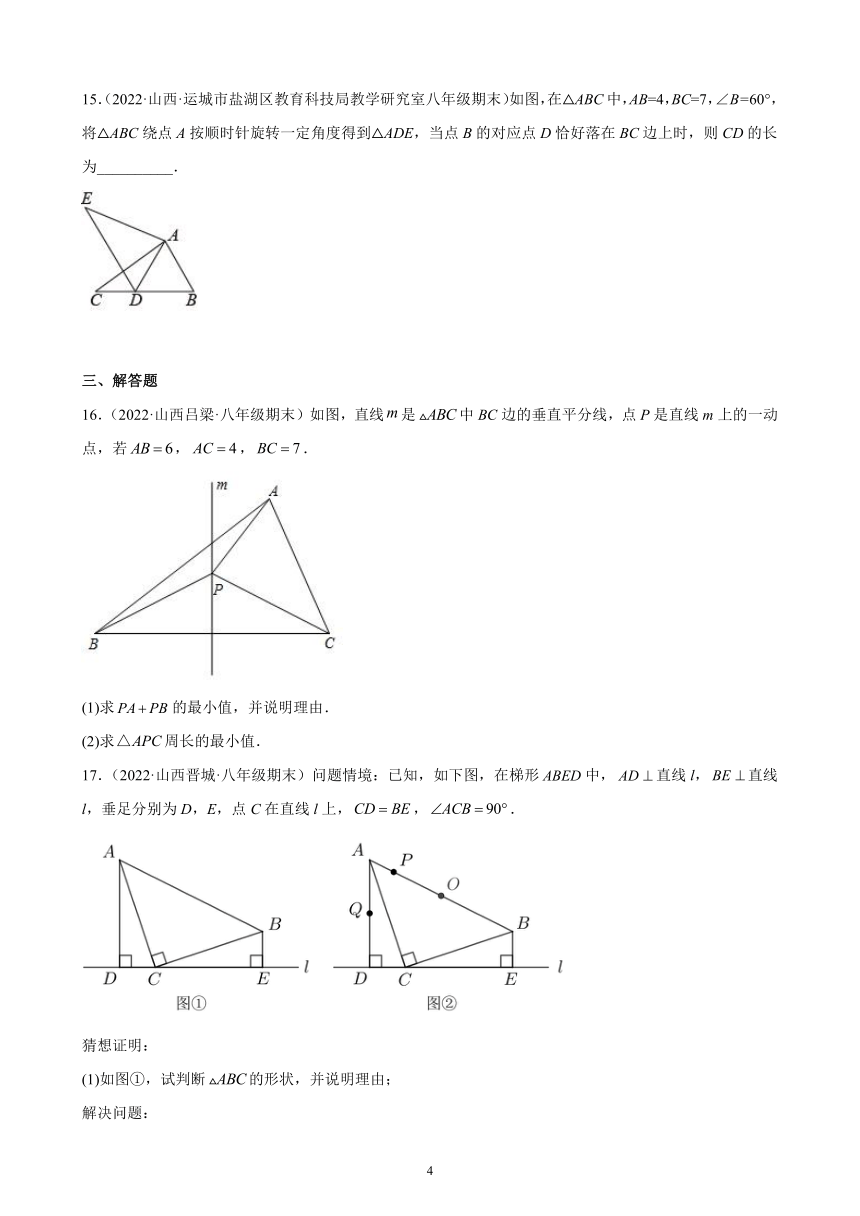
15.(2022·山西·运城市盐湖区教育科技局教学研究室八年级期末)如图,在△ABC中,AB=4,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为__________.
三、解答题
16.(2022·山西吕梁·八年级期末)如图,直线是中BC边的垂直平分线,点P是直线m上的一动点,若,,.
(1)求的最小值,并说明理由.
(2)求周长的最小值.
17.(2022·山西晋城·八年级期末)问题情境:已知,如下图,在梯形中,直线l,直线l,垂足分别为D,E,点C在直线l上,,.
猜想证明:
(1)如图①,试判断的形状,并说明理由;
解决问题:
(2)如图①,若,求梯形的面积;
拓展提升:
(3)如图②,设梯形的周长为m,边中点O处有两个动点P,Q同时出发,沿着的方向移动,点Q的速度是点P速度的3倍,当点P第一次到达点B时,两点同时停止移动.
①两点同时停止移动时,点Q移动的路程与点P移动的路程之差____________.(填“>”“<”或“=”)
②移动过程中点P能否和点Q相遇?如果能,则用直线a连接相遇点和点O,并探索直线a与的位置关系,写出推理过程:如不能,说明理由.
18.(2022·山西临汾·八年级期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,,则BE_________CF.
②如图2,若0°<∠BCA<180°,请添加一个关于与∠BCA关系的条件__________________,使①中的结论仍然成立,并说明理由;
(2)如图3.若线CD经过∠BCA的外部,,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由
19.(2022·山西太原·八年级期末)综合与实践:
已知,等腰三角形纸片ABC中,AB=AC,∠BAC=36°.现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应任务.
作法:如图1所示, ①分别作AB,AC的垂直平分线,交于点P; ②连接PA,PB,PC. 结论:沿线段PA,PB,PC剪开,即可得到三个等腰三角形, 理由:∵点P在线段AB的垂直平分线上, ∴_____(依据). 同理,PA=PC. ∴PA=PB=PC. ∴△PAB、△PBC、△PAC都是等腰三角形
任务:
(1)上述过程中,横线上的结论为_____,括号中的依据为_____.
(2)受小文的启发,同学们想到另一种思路:如图2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E.在此基础上构造两条线段(以图中标有字母的点为端点)作为裁剪线,也可解决问题!请在图2中画出一种裁剪方案,直接写出得到的三个等腰三角形及相应顶角的度数.
(3)如图3,等腰三角形纸片ABC中,AB=AC,∠BAC=108°,请从A,B两题中任选一题作答、我选择_____题.
A.请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
B.请在图3中设计出一种裁剪方案,将该三角形纸片分成四个等腰三角形,且四个三角形互不全等(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
20.(2022·山西运城·八年级期末)如图,在和中,,,,CE的延长线交BD于点F.
(1)求证:.
(2)若,请直接写出的度数.
(3)过点A作于点H,求证:.
21.(2022·山西晋中·八年级期末)如图,点 A,B,C,D 在同一条直线上,且 AB=CD,请从以下三个条件:①AE∥DF;②AE=DF;③EC=FB 中,再选两个作为已知条件,另一个作为结论, 推出一个正确的命题,并证明这个命题.
已知:AB=CD, , ;
求证: .(填写序号即可)
证明:
参考答案:
1.C
【解析】利用角平分线的性质可确定三角形中到三边距离相等的点满足的条件.
解:三角形三个内角的平分线的交点到三角形三边的距离相等.
故选:C.
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.掌握角平分线的性质是解题的关键.
2.B
【解析】利用等腰三角形的性质即可确定答案.
解:由题意可知,三角尺是等腰的,等腰三角形底边上的高与底边上的中线重合,若重锤的线经过三角尺底边的中点刻度,说明重锤与三角形底边上的高是重合的,而重锤是和水平面互相垂直的,所以说明此时的横梁是水平的,如果重锤的线没有经过三角尺底边的中点刻度,则说明横梁不是水平的, 因此能解释这一现象的数学知识是等腰三角形的三线合一.
故选:B.
本题考查等腰三角形的性质,理解等腰三角形三线合一(顶角平分线,底边上的中线,底边上的高相互重合)的性质是解题的关键.
3.B
【解析】根据线段垂直平分线的性质得到DA=DB=DC,根据等腰三角形的性质得到∠ACD=∠CAD=32°,∠DAB=∠DBA=28°,由三角形的内角和定理得到∠ADC=116°,∠ADB=124°,于是得到结论.
解:∵D是线段AC、AB的垂直平分线的交点,
∴DA=DB=DC,
∴∠ACD=∠CAD=32°,∠DAB=∠DBA=28°,
∴∠ADC=116°,∠ADB=124°,
∴∠CDB=120°,
∴∠BCD=(180°-120°)=30°,
故选:B.
本题考查了线段的垂直平分线的性质,解题的关键是根据线段的垂直平分线得到相等的线段.
4.C
【解析】根据等边对等角,可得∠ABD=∠A,根据角平分线的性质,∠ABD=∠CBD=,根据三角形内角和为180°列等式,将其它角都代换成计算即可.
∵BD=AD
∴∠ABD=∠A
∵BD平分
∴∠ABD=∠CBD=,
∴∠A=
∵,
∴
∴
故选 C.
本题考查三角形,掌握角平分线、等腰三角形的性质和三角形内角和定理是解题关键.
5.D
【解析】分三角形是锐角三角形或者钝角三角形两种情况进行讨论即可.
解:如图1,三角形是锐角三角形时,底角为
如图2,三角形是钝角三角形时,底角为
综上所述,它的底角为20°或70.
故选:D.
此题考查了等腰三角形的性质以及线段垂直平分线的性质,解题的关键是作出图形分情况进行讨论.
6.D
【解析】根据全等三角形的判定条件判断即可.
解:由题意可知
在中
∴(SSS)
∴
∴就是的平分线
故选:D
本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.
7.D
【解析】先根据等腰三角形的定义,分的内角为顶角和的内角为底角两种情况,再分别根据三角形的内角和定理即可得.
(1)当的内角为这个等腰三角形的顶角
则另外两个内角均为底角,它们的度数为
(2)当的内角为这个等腰三角形的底角
则另两个内角一个为底角,一个为顶角
底角为,顶角为
综上,另外两个内角的度数分别是或
故选:D.
本题考查了等腰三角形的定义、三角形的内角和定理,根据等腰三角形的定义,正确分两种情况讨论是解题关键.
8.D
【解析】过点D作DH⊥OB于点H,如图,根据角平分线的性质可得DH=DP=4,再根据三角形的面积即可求出结果.
解:过点D作DH⊥OB于点H,如图,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=4,
∴△ODQ的面积=.
故选:D.
本题主要考查了角平分线的性质,属于基本题型,熟练掌握角平分线的性质定理是解题关键.
9.C
【解析】利用基本作图得到AG平分∠BAC,利用角平分线的性质得到G点到AC的距离为1,然后根据三角形面积公式计算△ACG的面积.
解:由作法得平分,
点到的距离等于的长,即点到的距离为,
所以的面积.
故选C.
本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了交平分线的性质.
10.C
试题解析:∵OC平分∠AOB,
∴∠AOC=∠BOC;
又∵CD∥OB,
∴∠C=BOC,
∴∠C=∠AOC;
故选C.
11.20
【解析】过点D作于点H.由角平分线的性质可得出,利用“HL”分别证明,,再由全等三角形的面积相等即可求解.
如图,过点D作于点H.
∵AD是的角平分线,
∴.
又∵,,
∴(HL),
∴,
∴.
∵AD=AD,
∴(HL),
∴,
∴.
故答案为:20.
本题考查角平分线的性质定理,全等三角形的判定和性质.正确的作出辅助线构造全等三角形是解题关键.
12.3
【解析】根据垂直平分线的性质可得,根据平行线的性质可得,继而证明,得出,求得的长,即可求得的长.
解:∵是边上的中线,,
∴,
,
,
在与中
,
,
,,
,
.
故答案为:3.
本题考查了全等三角形的性质与判定,垂直平分线的性质,平行线的性质,综合运用以上知识是解题的关键.
13.47
【解析】根据旋转角的定义、旋转的性质、等腰三角形的性质以及三角形内角和定理进行解答.
解:∵秋千旋转了86°,小艾同学的位置也从A点运动到了A'点,
∴
∴
故答案为:47.
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.
14.∠B=∠C(答案不唯一)
【解析】求出BF=CE,再根据全等三角形的判定定理判断即可.
解:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
添加∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
故答案为:∠B=∠C(答案不唯一).
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键.
15.3
由旋转的性质可得:AD=AB,
,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=4,BC=7,
∴CD=BC BD=7 4=3.
故答案为:3.
16.(1)6,理由见解析
(2)10
【解析】(1)根据线段的性质即可得到结论;
(2)根据题意知点C关于直线m的对称点为点B,故当点P与点D重合时,AP+CP值的最小,求出AB长度即可得到结论.
(1)
解:当A,B,P三点共线时,PA+PB最小短
;
原因:两点之间,线段最短.
(2)
∵直线m是BC的垂直平分线,点P在m上,
∴点C关于直线m的对称点是点B,
则,
∵,
∵,
要使周长最小,
即最小,
当点P是直线m与AB的交点时,最小,
即,此时.
本题考查了轴对称一最短路线问题的应用,解此题的关键是找出P的位置.
17.(1)是等腰直角三角形,理由见解析
(2)32
(3)①=;②移动过程中点P能和Q点相遇,直线a垂直平分
【解析】(1)先得到,然后证明,得到,即可得到结论成立;
(2)由全等三角形的性质,得到,然后求出面积即可;
(3)①由动点的行程问题进行计算,即可得到答案;
②由题意可知,点Q比点P多走了一圈,然后列出等式,即可求出答案.
(1)
解:是等腰直角三角形.
理由:∵直线l,直线l,
∴;
又∵,
∴.
又∵,
∴.
在和中,
∴.
即:.
∴是等腰直角三角形.
(2)
解:根据(1)可得,
∴,
∴,
∴梯形的面积.
(3)
解:①∵点Q的速度是点P速度的3倍,
∴两点同时停止移动时,点Q移动的路程与点P移动的路程之差为;
故答案为:=;
②移动过程中点P能和Q点相遇.
设t秒后相遇,则点Q比点P多走一圈,
∴,
∴,
∴当点P走过的路程,与点Q相遇,
∵,
∴点P与边上的C点重合,连接,
∵且O为的中点,
∴直线a垂直平分.
本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,垂直平分线的判定,动点问题,解题的关键是熟练掌握所学的知识,正确的进行解题.
18.(1)①BE=CF;②,理由见解析
(2)EF=BE+AF,理由见解析
【解析】(1)①由∠BCA=90°,∠BEC=∠CFA=α=90°,可得∠CBE=∠ACF,从而可证△BCE≌△CAF,故BE=CF.
②若BE=CF,则可使得△BCE≌△CAF.根据题目已知条件添加条件,再使得一对角相等,△BCE≌△CAF便可得证.
(2)题干已知条件可证△BCE≌△CAF,故BE=CF,EC=FA,从而可证明EF=BE+AF.
(1)①∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°-∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
②α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°-∠BEC=180°-α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°-α.
又∵α+∠BCA=180°,
∴∠BCA=180°-α.
∴∠BCA=∠BCE+∠ACF=180°-α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
故答案为:①BE=CF;②
(2)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°-∠BCA=180°-α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°-∠BEC=180°-α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
19.(1)PA=PB;线段垂直平分线上的点到线段两个端点的距离相等
(2)△ADE的顶角为108°,△BDE的顶角为36°,△BDC的顶角为36°,或△ADE的顶角为108°,△BCE的顶角为72°,△DCE的顶角为144°
(3)A:作图见解析(方法不唯一);或B:作图见解析(方法不唯一)
【解析】(1)读懂推理过程即可完成;
(2)连接BD、CE,由作法及三角形内角和即可求得各等腰三角形顶角的度数;或连接DE、CE,由作法及三角形内角和即可求得各等腰三角形顶角的度数;
(3)选A:分别以B、C为圆心,AB长为半径画弧,两弧与BC相交,连接点A与这两个交点即可得到三个等腰三角形;
选B:以B为圆心,AB长为半径画弧,与BC相交于D,连接AD,在等腰△ABD中,利用图1或图2中的裁剪方法即可得到所要求的四个等腰三角形.
(1)
∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理,PA=PC.
∴PA=PB=PC.
∴△PAB、△PBC、△PAC都是等腰三角形.
故答案为:PA=PB;线段垂直平分线上的点到线段两个端点的距离相等
(2)
如图,连接BD、DE,由作法知,BC=BD=BE,则△BCD、△BDE是等腰三角形,
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
∵BC=BD,
∴∠BDC=∠ACB=72°,
∴∠DBC=36°,
∴∠EBD=∠ABC ∠DBC=36°,
∵BD=BE,
∴∠BED=∠BDE =72°,
∴∠AED=180° ∠BED=108°,
∴∠EDA=180° ∠BAC ∠AED=36°,
∴AE=DE,
即△ADE是等腰三角形.
综上,△ADE的顶角为108°,△BDE的顶角为36°,△BDC的顶角为36°;
如图,连接DE、CE,则BC=BE,
∴△BCE是等腰三角形,且顶角为72°,∠BEC=∠BCE=54°,
∴∠DCE=∠ACB←∠BCE=18°,
连接BD,由上一种裁剪方法知,BD平分∠ABC,
则△BCD≌△BED(SAS),
∴CD=DE,
即△DCE是等腰三角形,且顶角∠EDC=180° 2×18°=144°,
∴∠ADE=180° ∠EDC=36°=∠BAC,
∴AE=DE,
即△AED是等腰三角形,且顶角;
综上,△ADE的顶角为108°,△BCE的顶角为72°,△DCE的顶角为144°.
(3)
选A:分别以B、C为圆心,AB长为半径画弧,两弧与BC相交于点D、E,连接AD、AE 则△ABD、△ACE、△ADE三个三角形都是等腰三角形,如下图所示;
裁剪线段为AD、AE;
选B:以B为圆心,AB长为半径画弧,与BC相交于D,连接AD,对于等腰△ABD,按照图1中的裁剪方法,即可得到四个等腰三角形:△ACD、△ADE、△DEF、△BEF,其中裁剪线为AD、DE、EF.
本题考查了尺规作图、线段的垂直平分线性质定理、等腰三角形的判定与性质,掌握线段垂直平分线的性质定理、等腰三角形的判定与性质是关键.
20.(1)见解析
(2)50°
(3)见解析
【解析】(1)根据SAS可证得;
(2)由,可得,故,即可得出的度数;
(3)连接AF,过点A作于点J.由可得:,,即可得出.可证得,得:,由,可得出,即可证得结论.
(1)
证明:∵.
∴.
在和中,
,
∴.
(2)
∵,
∴,
∴.
∴,
∵,
∴.
故答案为:50°.
(3)
证明:如图,连接AF,过点A作于点J.
∵,
∴,,
∵,.
∴,
∴.
在和中,
,
∴,
∴.
在和中,
∴,
∴,
∴.
此题考查了全等的证明和性质,掌握全等的证明和性质是解题的关键.
21.①,②,③,证明见解析.
【解析】先确定选择哪对三角形,对应三角形全等条件求解,再根据全等三角形的性质解题.
已知:AB=CD, ① , ② ; 求证: ③
证明:
∵AB=CD
∴AB+BC=CD+BC,即 AC=DB
∵AE∥DF
∴∠A=∠D
又∵AE=DF
∴△ACE≌△DBF(SAS)
∴EC=FB
本题考查三角形全等的识别方法的开放性题目,答案可多种,掌握相关知识是解题关键.
一、单选题
1.(2022·山西临汾·八年级期末)三角形中,到三边距离相等的点是( )
A.三条高线所在直线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边的垂直平分线的交点
2.(2022·山西晋中·八年级期末)木工师傅将一个含45度角的三角尺和一个重锤如图放置,就能检查一根横梁是否水平,能解释这一现象的数学知识是( )
A.垂线段最短 B.等腰三角形的“三线合一”
C.角平分线的性质定理 D.线段垂直平分线的性质定理
3.(2022·山西晋中·八年级期末)如图,△ABC中,边AC,AB的垂直平分线相交于点D,若,,则的大小是( )
A.28° B.30° C.32° D.60°
4.(2022·山西运城·八年级期末)如图,在中,,BD平分交AC于点D.若,则的大小为( )
A.66° B.70° C.72° D.75°
5.(2022·山西吕梁·八年级期末)若等腰三角形一腰上的中垂线与另一腰所在直线相交,且交角为50°,则它的底角为( )
A.50° B.70° C.80° D.20°或70°
6.(2022·山西临汾·八年级期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.这里构造全等三角形的依据是( )
A. B. C. D.
7.(2022·山西晋城·八年级期末)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55° C.70°,40° D.55°,55°或70°,40°
8.(2022·山西临汾·八年级期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3 B.4
C.5 D.6
9.(2022·山西晋城·八年级期末)如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A. B. C. D.
10.(2022·山西吕梁·八年级期末)如图,已知OC平分∠AOB,CD//OB,若OD=3 cm,则CD等于:( )
A.1.5cm B.2cm C.3cm D.4cm
二、填空题
11.(2022·山西·运城市盐湖区教育科技局教学研究室八年级期末)如图,在中,AD是的角平分线,于E,F、G分别是边AB、AC上的点,连接DF、DG,且,和的面积分别为50和15,则的面积为________.
12.(2022·山西晋城·八年级期末)如图,在中,是边上的中线,E是边上一点,过点C作交的延长线于点F,当,,时,的长是____________.
13.(2022·山西晋中·八年级期末)如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则______度.
14.(2022·山西临汾·八年级期末)如图,点E,F在BC上,BE=CF,∠A=∠D.请添加一个条件________________,使△ABF≌△DCE
15.(2022·山西·运城市盐湖区教育科技局教学研究室八年级期末)如图,在△ABC中,AB=4,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为__________.
三、解答题
16.(2022·山西吕梁·八年级期末)如图,直线是中BC边的垂直平分线,点P是直线m上的一动点,若,,.
(1)求的最小值,并说明理由.
(2)求周长的最小值.
17.(2022·山西晋城·八年级期末)问题情境:已知,如下图,在梯形中,直线l,直线l,垂足分别为D,E,点C在直线l上,,.
猜想证明:
(1)如图①,试判断的形状,并说明理由;
解决问题:
(2)如图①,若,求梯形的面积;
拓展提升:
(3)如图②,设梯形的周长为m,边中点O处有两个动点P,Q同时出发,沿着的方向移动,点Q的速度是点P速度的3倍,当点P第一次到达点B时,两点同时停止移动.
①两点同时停止移动时,点Q移动的路程与点P移动的路程之差____________.(填“>”“<”或“=”)
②移动过程中点P能否和点Q相遇?如果能,则用直线a连接相遇点和点O,并探索直线a与的位置关系,写出推理过程:如不能,说明理由.
18.(2022·山西临汾·八年级期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,,则BE_________CF.
②如图2,若0°<∠BCA<180°,请添加一个关于与∠BCA关系的条件__________________,使①中的结论仍然成立,并说明理由;
(2)如图3.若线CD经过∠BCA的外部,,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由
19.(2022·山西太原·八年级期末)综合与实践:
已知,等腰三角形纸片ABC中,AB=AC,∠BAC=36°.现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应任务.
作法:如图1所示, ①分别作AB,AC的垂直平分线,交于点P; ②连接PA,PB,PC. 结论:沿线段PA,PB,PC剪开,即可得到三个等腰三角形, 理由:∵点P在线段AB的垂直平分线上, ∴_____(依据). 同理,PA=PC. ∴PA=PB=PC. ∴△PAB、△PBC、△PAC都是等腰三角形
任务:
(1)上述过程中,横线上的结论为_____,括号中的依据为_____.
(2)受小文的启发,同学们想到另一种思路:如图2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E.在此基础上构造两条线段(以图中标有字母的点为端点)作为裁剪线,也可解决问题!请在图2中画出一种裁剪方案,直接写出得到的三个等腰三角形及相应顶角的度数.
(3)如图3,等腰三角形纸片ABC中,AB=AC,∠BAC=108°,请从A,B两题中任选一题作答、我选择_____题.
A.请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
B.请在图3中设计出一种裁剪方案,将该三角形纸片分成四个等腰三角形,且四个三角形互不全等(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
20.(2022·山西运城·八年级期末)如图,在和中,,,,CE的延长线交BD于点F.
(1)求证:.
(2)若,请直接写出的度数.
(3)过点A作于点H,求证:.
21.(2022·山西晋中·八年级期末)如图,点 A,B,C,D 在同一条直线上,且 AB=CD,请从以下三个条件:①AE∥DF;②AE=DF;③EC=FB 中,再选两个作为已知条件,另一个作为结论, 推出一个正确的命题,并证明这个命题.
已知:AB=CD, , ;
求证: .(填写序号即可)
证明:
参考答案:
1.C
【解析】利用角平分线的性质可确定三角形中到三边距离相等的点满足的条件.
解:三角形三个内角的平分线的交点到三角形三边的距离相等.
故选:C.
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.掌握角平分线的性质是解题的关键.
2.B
【解析】利用等腰三角形的性质即可确定答案.
解:由题意可知,三角尺是等腰的,等腰三角形底边上的高与底边上的中线重合,若重锤的线经过三角尺底边的中点刻度,说明重锤与三角形底边上的高是重合的,而重锤是和水平面互相垂直的,所以说明此时的横梁是水平的,如果重锤的线没有经过三角尺底边的中点刻度,则说明横梁不是水平的, 因此能解释这一现象的数学知识是等腰三角形的三线合一.
故选:B.
本题考查等腰三角形的性质,理解等腰三角形三线合一(顶角平分线,底边上的中线,底边上的高相互重合)的性质是解题的关键.
3.B
【解析】根据线段垂直平分线的性质得到DA=DB=DC,根据等腰三角形的性质得到∠ACD=∠CAD=32°,∠DAB=∠DBA=28°,由三角形的内角和定理得到∠ADC=116°,∠ADB=124°,于是得到结论.
解:∵D是线段AC、AB的垂直平分线的交点,
∴DA=DB=DC,
∴∠ACD=∠CAD=32°,∠DAB=∠DBA=28°,
∴∠ADC=116°,∠ADB=124°,
∴∠CDB=120°,
∴∠BCD=(180°-120°)=30°,
故选:B.
本题考查了线段的垂直平分线的性质,解题的关键是根据线段的垂直平分线得到相等的线段.
4.C
【解析】根据等边对等角,可得∠ABD=∠A,根据角平分线的性质,∠ABD=∠CBD=,根据三角形内角和为180°列等式,将其它角都代换成计算即可.
∵BD=AD
∴∠ABD=∠A
∵BD平分
∴∠ABD=∠CBD=,
∴∠A=
∵,
∴
∴
故选 C.
本题考查三角形,掌握角平分线、等腰三角形的性质和三角形内角和定理是解题关键.
5.D
【解析】分三角形是锐角三角形或者钝角三角形两种情况进行讨论即可.
解:如图1,三角形是锐角三角形时,底角为
如图2,三角形是钝角三角形时,底角为
综上所述,它的底角为20°或70.
故选:D.
此题考查了等腰三角形的性质以及线段垂直平分线的性质,解题的关键是作出图形分情况进行讨论.
6.D
【解析】根据全等三角形的判定条件判断即可.
解:由题意可知
在中
∴(SSS)
∴
∴就是的平分线
故选:D
本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.
7.D
【解析】先根据等腰三角形的定义,分的内角为顶角和的内角为底角两种情况,再分别根据三角形的内角和定理即可得.
(1)当的内角为这个等腰三角形的顶角
则另外两个内角均为底角,它们的度数为
(2)当的内角为这个等腰三角形的底角
则另两个内角一个为底角,一个为顶角
底角为,顶角为
综上,另外两个内角的度数分别是或
故选:D.
本题考查了等腰三角形的定义、三角形的内角和定理,根据等腰三角形的定义,正确分两种情况讨论是解题关键.
8.D
【解析】过点D作DH⊥OB于点H,如图,根据角平分线的性质可得DH=DP=4,再根据三角形的面积即可求出结果.
解:过点D作DH⊥OB于点H,如图,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=4,
∴△ODQ的面积=.
故选:D.
本题主要考查了角平分线的性质,属于基本题型,熟练掌握角平分线的性质定理是解题关键.
9.C
【解析】利用基本作图得到AG平分∠BAC,利用角平分线的性质得到G点到AC的距离为1,然后根据三角形面积公式计算△ACG的面积.
解:由作法得平分,
点到的距离等于的长,即点到的距离为,
所以的面积.
故选C.
本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了交平分线的性质.
10.C
试题解析:∵OC平分∠AOB,
∴∠AOC=∠BOC;
又∵CD∥OB,
∴∠C=BOC,
∴∠C=∠AOC;
故选C.
11.20
【解析】过点D作于点H.由角平分线的性质可得出,利用“HL”分别证明,,再由全等三角形的面积相等即可求解.
如图,过点D作于点H.
∵AD是的角平分线,
∴.
又∵,,
∴(HL),
∴,
∴.
∵AD=AD,
∴(HL),
∴,
∴.
故答案为:20.
本题考查角平分线的性质定理,全等三角形的判定和性质.正确的作出辅助线构造全等三角形是解题关键.
12.3
【解析】根据垂直平分线的性质可得,根据平行线的性质可得,继而证明,得出,求得的长,即可求得的长.
解:∵是边上的中线,,
∴,
,
,
在与中
,
,
,,
,
.
故答案为:3.
本题考查了全等三角形的性质与判定,垂直平分线的性质,平行线的性质,综合运用以上知识是解题的关键.
13.47
【解析】根据旋转角的定义、旋转的性质、等腰三角形的性质以及三角形内角和定理进行解答.
解:∵秋千旋转了86°,小艾同学的位置也从A点运动到了A'点,
∴
∴
故答案为:47.
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.
14.∠B=∠C(答案不唯一)
【解析】求出BF=CE,再根据全等三角形的判定定理判断即可.
解:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
添加∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
故答案为:∠B=∠C(答案不唯一).
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键.
15.3
由旋转的性质可得:AD=AB,
,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=4,BC=7,
∴CD=BC BD=7 4=3.
故答案为:3.
16.(1)6,理由见解析
(2)10
【解析】(1)根据线段的性质即可得到结论;
(2)根据题意知点C关于直线m的对称点为点B,故当点P与点D重合时,AP+CP值的最小,求出AB长度即可得到结论.
(1)
解:当A,B,P三点共线时,PA+PB最小短
;
原因:两点之间,线段最短.
(2)
∵直线m是BC的垂直平分线,点P在m上,
∴点C关于直线m的对称点是点B,
则,
∵,
∵,
要使周长最小,
即最小,
当点P是直线m与AB的交点时,最小,
即,此时.
本题考查了轴对称一最短路线问题的应用,解此题的关键是找出P的位置.
17.(1)是等腰直角三角形,理由见解析
(2)32
(3)①=;②移动过程中点P能和Q点相遇,直线a垂直平分
【解析】(1)先得到,然后证明,得到,即可得到结论成立;
(2)由全等三角形的性质,得到,然后求出面积即可;
(3)①由动点的行程问题进行计算,即可得到答案;
②由题意可知,点Q比点P多走了一圈,然后列出等式,即可求出答案.
(1)
解:是等腰直角三角形.
理由:∵直线l,直线l,
∴;
又∵,
∴.
又∵,
∴.
在和中,
∴.
即:.
∴是等腰直角三角形.
(2)
解:根据(1)可得,
∴,
∴,
∴梯形的面积.
(3)
解:①∵点Q的速度是点P速度的3倍,
∴两点同时停止移动时,点Q移动的路程与点P移动的路程之差为;
故答案为:=;
②移动过程中点P能和Q点相遇.
设t秒后相遇,则点Q比点P多走一圈,
∴,
∴,
∴当点P走过的路程,与点Q相遇,
∵,
∴点P与边上的C点重合,连接,
∵且O为的中点,
∴直线a垂直平分.
本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,垂直平分线的判定,动点问题,解题的关键是熟练掌握所学的知识,正确的进行解题.
18.(1)①BE=CF;②,理由见解析
(2)EF=BE+AF,理由见解析
【解析】(1)①由∠BCA=90°,∠BEC=∠CFA=α=90°,可得∠CBE=∠ACF,从而可证△BCE≌△CAF,故BE=CF.
②若BE=CF,则可使得△BCE≌△CAF.根据题目已知条件添加条件,再使得一对角相等,△BCE≌△CAF便可得证.
(2)题干已知条件可证△BCE≌△CAF,故BE=CF,EC=FA,从而可证明EF=BE+AF.
(1)①∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°-∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
②α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°-∠BEC=180°-α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°-α.
又∵α+∠BCA=180°,
∴∠BCA=180°-α.
∴∠BCA=∠BCE+∠ACF=180°-α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
故答案为:①BE=CF;②
(2)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°-∠BCA=180°-α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°-∠BEC=180°-α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
19.(1)PA=PB;线段垂直平分线上的点到线段两个端点的距离相等
(2)△ADE的顶角为108°,△BDE的顶角为36°,△BDC的顶角为36°,或△ADE的顶角为108°,△BCE的顶角为72°,△DCE的顶角为144°
(3)A:作图见解析(方法不唯一);或B:作图见解析(方法不唯一)
【解析】(1)读懂推理过程即可完成;
(2)连接BD、CE,由作法及三角形内角和即可求得各等腰三角形顶角的度数;或连接DE、CE,由作法及三角形内角和即可求得各等腰三角形顶角的度数;
(3)选A:分别以B、C为圆心,AB长为半径画弧,两弧与BC相交,连接点A与这两个交点即可得到三个等腰三角形;
选B:以B为圆心,AB长为半径画弧,与BC相交于D,连接AD,在等腰△ABD中,利用图1或图2中的裁剪方法即可得到所要求的四个等腰三角形.
(1)
∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理,PA=PC.
∴PA=PB=PC.
∴△PAB、△PBC、△PAC都是等腰三角形.
故答案为:PA=PB;线段垂直平分线上的点到线段两个端点的距离相等
(2)
如图,连接BD、DE,由作法知,BC=BD=BE,则△BCD、△BDE是等腰三角形,
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
∵BC=BD,
∴∠BDC=∠ACB=72°,
∴∠DBC=36°,
∴∠EBD=∠ABC ∠DBC=36°,
∵BD=BE,
∴∠BED=∠BDE =72°,
∴∠AED=180° ∠BED=108°,
∴∠EDA=180° ∠BAC ∠AED=36°,
∴AE=DE,
即△ADE是等腰三角形.
综上,△ADE的顶角为108°,△BDE的顶角为36°,△BDC的顶角为36°;
如图,连接DE、CE,则BC=BE,
∴△BCE是等腰三角形,且顶角为72°,∠BEC=∠BCE=54°,
∴∠DCE=∠ACB←∠BCE=18°,
连接BD,由上一种裁剪方法知,BD平分∠ABC,
则△BCD≌△BED(SAS),
∴CD=DE,
即△DCE是等腰三角形,且顶角∠EDC=180° 2×18°=144°,
∴∠ADE=180° ∠EDC=36°=∠BAC,
∴AE=DE,
即△AED是等腰三角形,且顶角;
综上,△ADE的顶角为108°,△BCE的顶角为72°,△DCE的顶角为144°.
(3)
选A:分别以B、C为圆心,AB长为半径画弧,两弧与BC相交于点D、E,连接AD、AE 则△ABD、△ACE、△ADE三个三角形都是等腰三角形,如下图所示;
裁剪线段为AD、AE;
选B:以B为圆心,AB长为半径画弧,与BC相交于D,连接AD,对于等腰△ABD,按照图1中的裁剪方法,即可得到四个等腰三角形:△ACD、△ADE、△DEF、△BEF,其中裁剪线为AD、DE、EF.
本题考查了尺规作图、线段的垂直平分线性质定理、等腰三角形的判定与性质,掌握线段垂直平分线的性质定理、等腰三角形的判定与性质是关键.
20.(1)见解析
(2)50°
(3)见解析
【解析】(1)根据SAS可证得;
(2)由,可得,故,即可得出的度数;
(3)连接AF,过点A作于点J.由可得:,,即可得出.可证得,得:,由,可得出,即可证得结论.
(1)
证明:∵.
∴.
在和中,
,
∴.
(2)
∵,
∴,
∴.
∴,
∵,
∴.
故答案为:50°.
(3)
证明:如图,连接AF,过点A作于点J.
∵,
∴,,
∵,.
∴,
∴.
在和中,
,
∴,
∴.
在和中,
∴,
∴,
∴.
此题考查了全等的证明和性质,掌握全等的证明和性质是解题的关键.
21.①,②,③,证明见解析.
【解析】先确定选择哪对三角形,对应三角形全等条件求解,再根据全等三角形的性质解题.
已知:AB=CD, ① , ② ; 求证: ③
证明:
∵AB=CD
∴AB+BC=CD+BC,即 AC=DB
∵AE∥DF
∴∠A=∠D
又∵AE=DF
∴△ACE≌△DBF(SAS)
∴EC=FB
本题考查三角形全等的识别方法的开放性题目,答案可多种,掌握相关知识是解题关键.
