数学人教A版(2019)选择性必修第二册4.1.1 数列的概念与简单表示法(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.1.1 数列的概念与简单表示法(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 13:26:57 | ||
图片预览








文档简介
(共22张PPT)
4.1.1 数列的概念与简单表示法
第二章 数列
情景引入
古语云:“勤学如春起之苗,不见其增,日有所长”如果对“春起之苗”每日用精密仪器度量,则每日的高度值按日期排在一起,可组成一个数列. 那么什么叫数列呢
探究新知
1. 王芳从一岁到17岁,每年生日那天测量身高,将这些身高数据(单位:厘米)依次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168 ①
记王芳第的身高为,那么=75 , =87, =168.我们发现中的反映了身高按岁数从1到17的顺序排列时的确定位置,即=75 是排在第1位的数,=87是排在第2位的数 =168是排在第17位的数,它们之间不能交换位置,所以①具有确定顺序的一列数.
探究新知
2. 在两河流域发掘的一块泥板(编号K90,约生产于公元
前7世纪)上,有一列依次表示一个月中从第1天到第15天,
每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240. ②
记第月亮可见部分的数为, 那么=5 , =10, =240.这里,中的反映了月亮可见部分的数按日期从1~15顺序排列时的确定位置,即=5是排在第1位的数,=10是排在第2位的数=240是排在第15位的数,它们之间不能交换位置,所以,②也是具有确定顺序的一列数.
探究新知
3.的次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
,,,,…. ③
思考:你能仿照上面的叙述,说明③也是具有确定顺序的一列数吗?
记第个数为,那么,,,,….这里,中的反映了的次幂按1次幂、2次幂、3次幂、4次幂……的顺序排列时的确定位置,即是排在第1位的数,是排在第2位的数,是排在第3位的数,…,它们之间不能交换位置.
所以③是具有确定顺序的一列数.
归纳: 上述例子的共同特征是什么?
探究新知
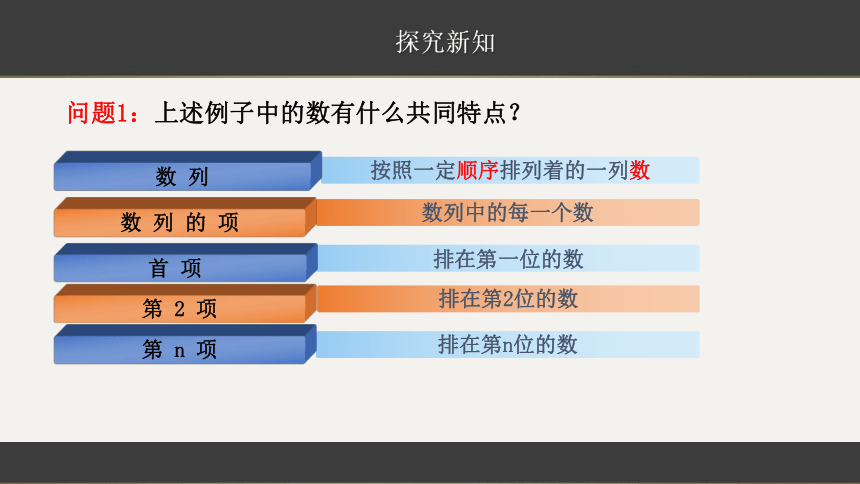
按照一定顺序排列着的一列数
数列中的每一个数
排在第一位的数
排在第2位的数
排在第n位的数
数 列
数 列 的 项
首 项
第 2 项
第 n 项
问题1:上述例子中的数有什么共同特点?
探究新知
思考1:数列③ ,35 改为 3,2,1, 35
请问:是不是同一数列?
不是
思考1:数列④ 改为 1,-1,1,
请问:是不是同一数列?
不是
探究新知
(辨析数列的概念:)
(1) “1, 2, 3, 4, 5”与“5, 4, 3, 2, 1”是同一个数列吗?与“1, 3, 2, 4, 5呢?
——数列的有序性
(2) 数列中的数可以重复吗?
问题2:数列与集合有什么区别?
集合讲究:无序性、互异性、确定性,
——可重复
数列讲究:有序性、可重复性、确定性.
探究新知
数列的一般形式可以写成:
简记为 ,其中叫做数列的第n 项.
思考: {an} 与an的意思一样吗?
{an}表示一个数列:a1,a2,a3,…,an,…. ;
an表示数列{an}中的第n项.
探究新知
问题3:数列如何分类?
(1)按项数分:
项数有限的数列叫有穷数列
项数无限的数列叫无穷数列
(2)按项之间的大小关系:
递增数列,
递减数列,
摆动数列,
常数列。
有穷数列
无穷数列
有穷数列
无穷数列
无穷数列
递增数列
递增数列
递减数列
摆动数列
常数列
探究新知
CCTV-2中央电视台开心辞典节目中曾经出现过这样的一道题:
观察以下几个数的特点,按照其中的规律写出括号里的数.
37
2,5,10,17,26, ( ) , 50 , ...
项
序号 1 2 3 4 5 6 7 ... n
n
a
=
2
n
+1
通项公式
通项公式的概念:
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
探究新知
第1项
第2项
第3项
第n项
或
探究新知
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.
项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)
(函数值)
通项公式
探究新知
问题4:你能从中得到什么启示?数列的实质是什么?
y=f(x)
an
n
函数值
自变量
项
通项公式
序号(正整数或它的有限子集)
数列的项 是n的函数可以认为数列是一种特殊的函数.
函数解析式 =就是数列的通项公式.
以前我们学过的函数的自变量通常是连续变化.的,而数列是自变量为离散的数的函数.
探究新知
问题5:数列有哪些表示方法?
1、通项公式法
2、图象法
{
3、列表法
数列的表示法:
你能做出下列两个数列的图象吗?
(1)全体正偶数按从小到大顺序构成的数列 :
2,4,6,8,……,2n,…
(2)正方形数构成的数列 1,4,9,16,…,n2 ,…
探究新知
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
0
是些孤立点
探究新知
1
2
3
4
1
2
3
4
5
6
7
8
9
0
-1
2
探究新知
1
2
3
4
5
1
2
3
4
5
0
-1
我们好孤单!
我们好孤单!
数列用图象表示时的特点——一群孤立的点
数列是定义域为正整数集或是它的有限子集{1,2,3,……n }的函数.
探究新知
例1. 根据下列数列{an}的通项公式,写出数列的前5项,并画出它们的图象.
探究新知
例2.写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(3)9,99,999,9 999.
思 考 :
根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明.
?
注意:①一些数列的通项公式不是唯一的
②不是每一个数列都能写出它的通项公式
③
练一练
探究新知
写出下列数列的一个通项公式,使它的前4项分别是下列各数:
(3) 0,1,0,1;
课堂小结
常见数列通项公式求法:
(1)常见数列:正整数列,奇数列,偶数列,平方数列等直接写通项公式;
(2) 分数列:观察分子、分母的特点后写通项公式;
(3) 指数数列:观察底数、指数的特点后写通项公式;
(4) 各项符号一正一负:
4.1.1 数列的概念与简单表示法
第二章 数列
情景引入
古语云:“勤学如春起之苗,不见其增,日有所长”如果对“春起之苗”每日用精密仪器度量,则每日的高度值按日期排在一起,可组成一个数列. 那么什么叫数列呢
探究新知
1. 王芳从一岁到17岁,每年生日那天测量身高,将这些身高数据(单位:厘米)依次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168 ①
记王芳第的身高为,那么=75 , =87, =168.我们发现中的反映了身高按岁数从1到17的顺序排列时的确定位置,即=75 是排在第1位的数,=87是排在第2位的数 =168是排在第17位的数,它们之间不能交换位置,所以①具有确定顺序的一列数.
探究新知
2. 在两河流域发掘的一块泥板(编号K90,约生产于公元
前7世纪)上,有一列依次表示一个月中从第1天到第15天,
每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240. ②
记第月亮可见部分的数为, 那么=5 , =10, =240.这里,中的反映了月亮可见部分的数按日期从1~15顺序排列时的确定位置,即=5是排在第1位的数,=10是排在第2位的数=240是排在第15位的数,它们之间不能交换位置,所以,②也是具有确定顺序的一列数.
探究新知
3.的次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
,,,,…. ③
思考:你能仿照上面的叙述,说明③也是具有确定顺序的一列数吗?
记第个数为,那么,,,,….这里,中的反映了的次幂按1次幂、2次幂、3次幂、4次幂……的顺序排列时的确定位置,即是排在第1位的数,是排在第2位的数,是排在第3位的数,…,它们之间不能交换位置.
所以③是具有确定顺序的一列数.
归纳: 上述例子的共同特征是什么?
探究新知
按照一定顺序排列着的一列数
数列中的每一个数
排在第一位的数
排在第2位的数
排在第n位的数
数 列
数 列 的 项
首 项
第 2 项
第 n 项
问题1:上述例子中的数有什么共同特点?
探究新知
思考1:数列③ ,35 改为 3,2,1, 35
请问:是不是同一数列?
不是
思考1:数列④ 改为 1,-1,1,
请问:是不是同一数列?
不是
探究新知
(辨析数列的概念:)
(1) “1, 2, 3, 4, 5”与“5, 4, 3, 2, 1”是同一个数列吗?与“1, 3, 2, 4, 5呢?
——数列的有序性
(2) 数列中的数可以重复吗?
问题2:数列与集合有什么区别?
集合讲究:无序性、互异性、确定性,
——可重复
数列讲究:有序性、可重复性、确定性.
探究新知
数列的一般形式可以写成:
简记为 ,其中叫做数列的第n 项.
思考: {an} 与an的意思一样吗?
{an}表示一个数列:a1,a2,a3,…,an,…. ;
an表示数列{an}中的第n项.
探究新知
问题3:数列如何分类?
(1)按项数分:
项数有限的数列叫有穷数列
项数无限的数列叫无穷数列
(2)按项之间的大小关系:
递增数列,
递减数列,
摆动数列,
常数列。
有穷数列
无穷数列
有穷数列
无穷数列
无穷数列
递增数列
递增数列
递减数列
摆动数列
常数列
探究新知
CCTV-2中央电视台开心辞典节目中曾经出现过这样的一道题:
观察以下几个数的特点,按照其中的规律写出括号里的数.
37
2,5,10,17,26, ( ) , 50 , ...
项
序号 1 2 3 4 5 6 7 ... n
n
a
=
2
n
+1
通项公式
通项公式的概念:
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
探究新知
第1项
第2项
第3项
第n项
或
探究新知
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.
项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)
(函数值)
通项公式
探究新知
问题4:你能从中得到什么启示?数列的实质是什么?
y=f(x)
an
n
函数值
自变量
项
通项公式
序号(正整数或它的有限子集)
数列的项 是n的函数可以认为数列是一种特殊的函数.
函数解析式 =就是数列的通项公式.
以前我们学过的函数的自变量通常是连续变化.的,而数列是自变量为离散的数的函数.
探究新知
问题5:数列有哪些表示方法?
1、通项公式法
2、图象法
{
3、列表法
数列的表示法:
你能做出下列两个数列的图象吗?
(1)全体正偶数按从小到大顺序构成的数列 :
2,4,6,8,……,2n,…
(2)正方形数构成的数列 1,4,9,16,…,n2 ,…
探究新知
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
0
是些孤立点
探究新知
1
2
3
4
1
2
3
4
5
6
7
8
9
0
-1
2
探究新知
1
2
3
4
5
1
2
3
4
5
0
-1
我们好孤单!
我们好孤单!
数列用图象表示时的特点——一群孤立的点
数列是定义域为正整数集或是它的有限子集{1,2,3,……n }的函数.
探究新知
例1. 根据下列数列{an}的通项公式,写出数列的前5项,并画出它们的图象.
探究新知
例2.写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(3)9,99,999,9 999.
思 考 :
根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明.
?
注意:①一些数列的通项公式不是唯一的
②不是每一个数列都能写出它的通项公式
③
练一练
探究新知
写出下列数列的一个通项公式,使它的前4项分别是下列各数:
(3) 0,1,0,1;
课堂小结
常见数列通项公式求法:
(1)常见数列:正整数列,奇数列,偶数列,平方数列等直接写通项公式;
(2) 分数列:观察分子、分母的特点后写通项公式;
(3) 指数数列:观察底数、指数的特点后写通项公式;
(4) 各项符号一正一负:
