人教A版(2019)数学必修第二册8_6_3平面与平面垂直课件(共39张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第二册8_6_3平面与平面垂直课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 13:36:48 | ||
图片预览





文档简介
(共39张PPT)
平面与平面垂直
本节目标
学 习 目 标 核 心 素 养
1.理解二面角的有关概念,会作二面角的平面角,能求简单二面角平面角的大小.(难点、易错点) 2.了解面面垂直的定义,掌握面面垂直的判定定理和性质定理,初步学会用定理证明垂直关系.(重点) 3.熟悉线线垂直、线面垂直的转化.(重点) 1. 通过学习面面垂直的判定定理和性质定理,提升直观想象、逻辑推理的数学素养.
2. 通过学习二面角,提升直观想象、逻辑推理、数学运算的数学素养.
课前预习
预习课本P155~161,思考并完成以下问题
1.什么叫做二面角?什么叫做二面角的平面角?
2.两个平面互相垂直是怎样定义的?两个平面互相垂直的判定定理是什么?
3.平面与平面垂直的性质定理是什么?
课前小测
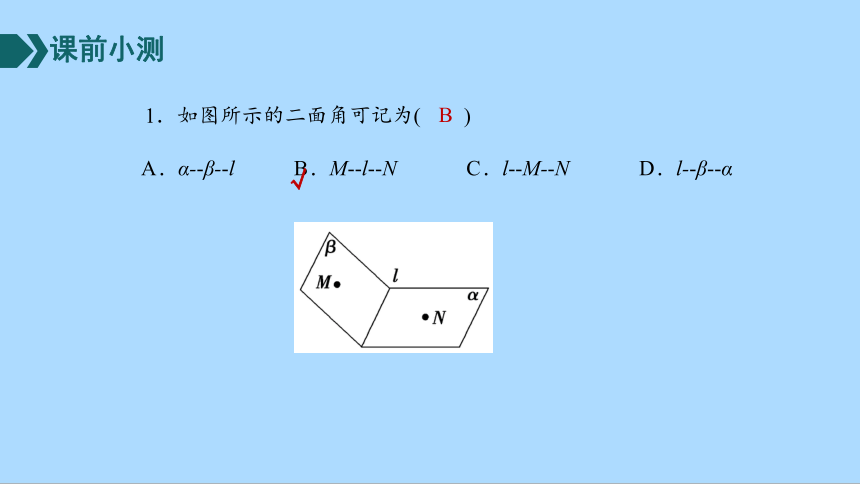
1.如图所示的二面角可记为( )
A.α- β- l B.M -l -N C.l -M- N D.l- β -α
B
√
2.已知直线l⊥平面α,则经过l且和α垂直的平面( )
A.有一个 B.有两个
C.有无数个 D.不存在
C
经过l的任一平面都和α垂直
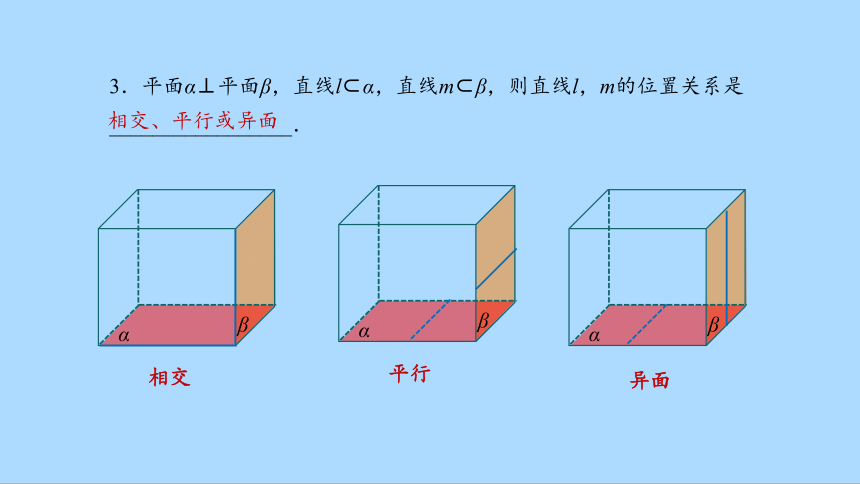
3.平面α⊥平面β,直线l α,直线m β,则直线l,m的位置关系是_________________.
α
β
相交
α
β
平行
α
β
异面
相交、平行或异面
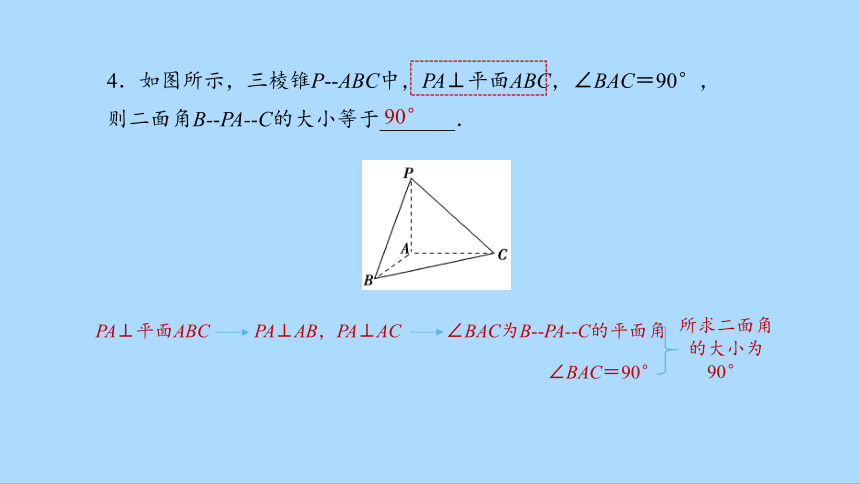
4.如图所示,三棱锥P -ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B- PA- C的大小等于_______.
PA⊥平面ABC
PA⊥AB,PA⊥AC
∠BAC为B -PA- C的平面角
∠BAC=90°
所求二面角的大小为90°
90°
考点精讲
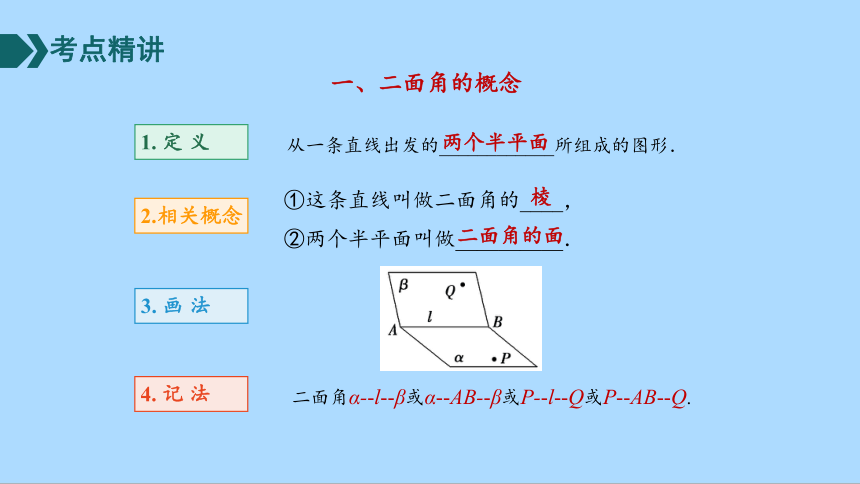
一、二面角的概念
1. 定 义
从一条直线出发的____________所组成的图形.
①这条直线叫做二面角的____,
②两个半平面叫做__________.
2.相关概念
两个半平面
棱
二面角的面
3. 画 法
4. 记 法
二面角α- l -β或α -AB- β或P- l -Q或P -AB -Q.
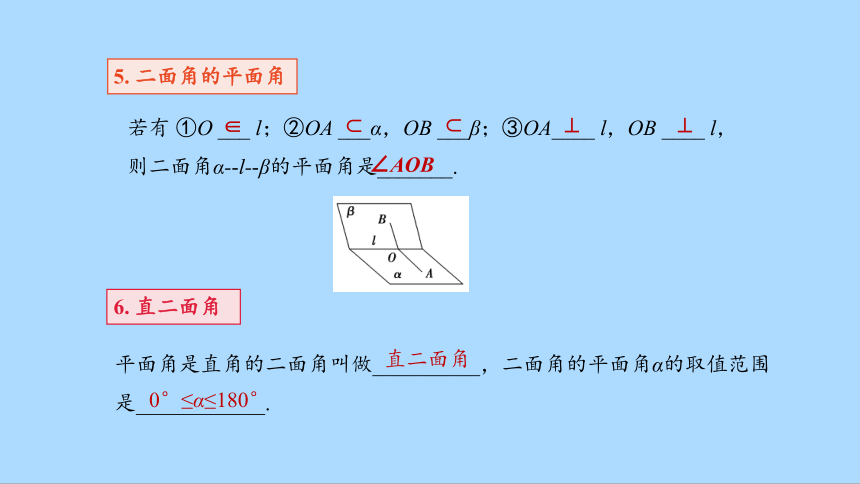
5. 二面角的平面角
若有 ①O ___ l;②OA ___α,OB ___β;③OA____ l,OB ____ l,
则二面角α- l- β的平面角是_______.
∈
⊥
⊥
∠AOB
6. 直二面角
平面角是直角的二面角叫做__________,二面角的平面角α的取值范围是____________.
直二面角
0°≤α≤180°
思考1:二面角的平面角的大小,是否与角的顶点在棱上的位置有关?
提示: 无关.如图,根据等角定理可知,∠AOB=∠A′O′B′,即二面角的平面角的大小与角的顶点的位置无关,只与二面角的大小有关.
二、平面与平面垂直
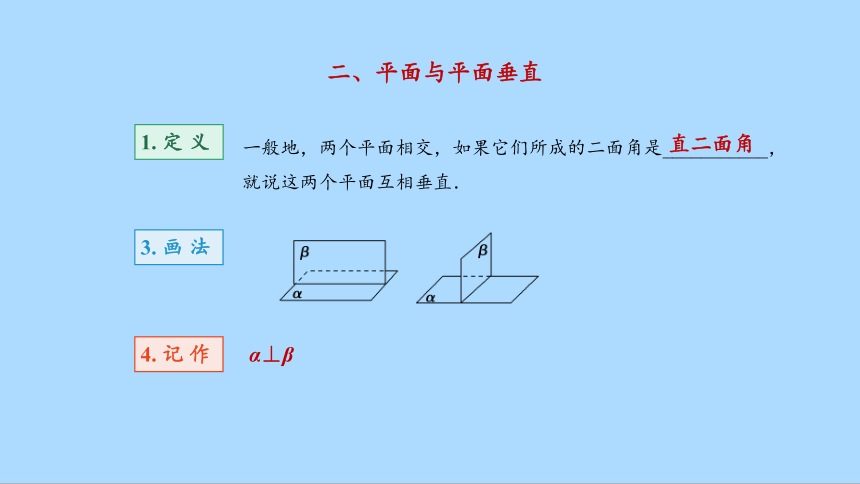
1. 定 义
3. 画 法
4. 记 作
一般地,两个平面相交,如果它们所成的二面角是___________,就说这两个平面互相垂直.
直二面角
α⊥β
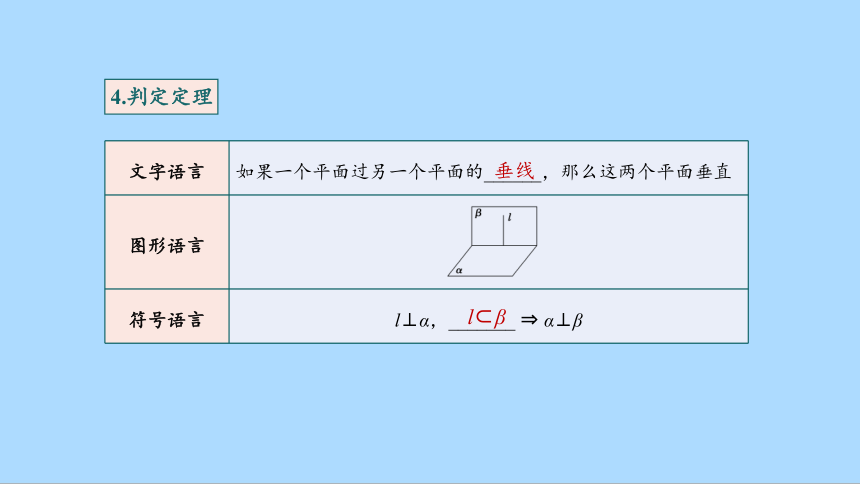
4.判定定理
文字语言 如果一个平面过另一个平面的______,那么这两个平面垂直
图形语言
符号语言 l⊥α,_______ α⊥β
垂线
l β
思考2:两个平面垂直,则一个平面内的任何一条直线都垂直于另一个平面吗?
提示:不一定,只有在一个平面内垂直于交线的直线才垂直于另一个平面.
三.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的_______,那么这条直线与另一个平面________.
符号语言 a⊥β
图形语言
作用 ①面面垂直 ________垂直
②作面的垂线
交线
垂直
线面
思考3:如果α⊥β,则α内的直线必垂直于β内的无数条直线吗?
提示:正确.若设α∩β=l,a α,b β,b⊥l,则a⊥b,故β内与b平行的无数条直线均垂直于α内的任意直线.
题型一 二面角的计算问题
典例剖析
【例1】如图,已知三棱锥A -BCD的各棱长均为2,求二面角A -CD- B的余弦值.
M
H
如图,取CD的中点M,连接AM,BM,则AM⊥CD,BM⊥CD.
由二面角的定义可知∠AMB为二面角A CD B的平面角.
方法技巧
1
2
3
1.求二面角大小的步骤
找出这个平面角;
证明这个角是二面角的平面角;
作出这个角所在的三角形,解这个三角形,求出角的大小.
2.确定二面角的平面角的方法
过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角,如图所示.
定义法
在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.
垂面法
活学活用
1.如图,AC⊥平面BCD,BD⊥CD, AC= AD,求平面 ABD 与平面BCD 所成的二面角的大小.
因为AC⊥平面 BCD,BD 平面 BCD,所以BD⊥AC.
又因为BD⊥CD,AC∩CD=C,
所以BD⊥平面 ACD.
因为AD 平面 ACD,所以AD⊥BD,
所以∠ADC即为平面 ABD 与平面 BCD 所成二面角的平面角.
在Rt△ACD中,AC= AD,所以∠ADC=30°.
题型二 平面与平面垂直的判定
【例2】 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC. 求证:平面ABC⊥平面SBC.
∠BSA=∠CSA=60°,SA=SB=SC,所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.取BC的中点D,如图所示,
连接AD,SD,则AD⊥BC,SD⊥BC,所以∠ADS为二面角A -BC- S的平面角.
在Rt△BSC中,因为SB=SC=a,所以SD= a,BD= a.
在Rt△ABD中,AD= a,在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A -BC -S为直二面角,故平面ABC⊥平面SBC.
法一
【例2】 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC. 求证:平面ABC⊥平面SBC.
法二
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
因为△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又因为AD 平面ABC,所以平面ABC⊥平面SBC.
方法技巧
证明面面垂直常用的方法
两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
定义法
即说明两个半平面所成的二面角是直二面角
判定定理法
在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为线面垂直;
性质法
活学活用
2.如图所示,四边形ABCD是边长为a的菱形,PC⊥平面ABCD,E是PA的中点,求证:平面BDE⊥平面ABCD.
连接AC,设AC∩BD=O,连接OE.
因为O为AC中点,E为PA的中点,
所以EO是△PAC的中位线,
所以EO∥PC.
因为PC⊥平面ABCD,所以EO⊥平面ABCD.
又因为EO 平面BDE,
所以平面BDE⊥平面ABCD.
题型三 面面垂直性质定理的应用
【例3】如图,在三棱锥P -ABC中,PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥AB.
如图,在平面PAB内,作AD⊥PB于点D.
平面PAB⊥平面PBC
平面PAB∩平面PBC=PB
AD 平面PAB
AD⊥PB
AD⊥平面PBC
BC 平面PBC
AD⊥BC
PA⊥平面ABC,BC 平面ABC
PA⊥BC
PA∩AD=A
BC⊥平面PAB
AB 平面PAB
BC⊥AB
方法技巧
(1) 线面垂直的判定定理;
(2) 面面垂直的性质定理;
(3) 若a∥b,a⊥α,则b⊥α (a、b为直线,α为平面);
(4) 若a⊥α,α∥β,则a⊥β (a为直线,α,β为平面);
证明或判定线面垂直的常用方法
∵平面VAB⊥平面ABCD,且BC⊥AB,平面VAB∩平面ABCD=AB,BC 平面ABCD.
∴BC⊥平面VAB,
又VA 平面VAB,∴BC⊥VA,
又VB⊥平面VAD,∴VB⊥VA,
又VB∩BC=B,∴VA⊥平面VBC,
∵VA 平面VAC,∴平面VBC⊥平面VAC.
活学活用
3.如图,四棱锥V- ABCD的底面是矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD. 求证:平面VBC⊥平面VAC.
难点突破
[探究问题]
试总结线线垂直、线面垂直、面面垂直之间的转化关系.
[提示] 垂直问题转化关系如下所示:
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:(1)DE=DA;
设BD=a,如图,作DF∥BC交CE于F,
则CF=DB=a.因为CE⊥平面ABC,
所以BC⊥CF,DF⊥EC,
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(2)平面BDM⊥平面ECA;
取CA的中点N,连接MN,BN,则
所以四边形MNBD为平行四边形,所以MD∥BN.
又因为EC⊥平面ABC,所以EC⊥BN,EC⊥MD.
又DE=DA,M为EA的中点,所以DM⊥AE.
所以DM⊥平面AEC,所以平面BDM⊥平面ECA.
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(3)平面DEA⊥平面ECA.
由(2)知DM⊥平面AEC,而DM 平面DEA,
所以平面DEA⊥平面ECA.
活学活用
4、本例条件不变,试求平面ADE与平面ABC所成二面角的大小.
如图延长ED交CB延长线于点N,连接AN,设BD=a,由例题知,CE=AC=BC=AB=2a,
在△CEN中,由知B为CN中点,∴CB=BN=2a.
∴△ABN中,∠ABN=120°,∠BAN=∠BNA=30°,
∴∠CAN=90°,即NA⊥CA.
又EC⊥平面ABC,∴EC⊥NA,又CA∩CE=C,
∴NA⊥平面ACE,∴NA⊥AE,NA⊥AC,且AN为平面ADE与平面ABC的交线.
∴∠CAE为平面ADE与平面ABC所成二面角的平面角,
在Rt△ACE中,AC=CE,∴∠CAE=45°.
所以平面ADE与平面ABC所成二面角为45°.
方法技巧
垂直关系的互化及解题策略
空间问题化成平面问题是解决立体几何问题的一个基本原则,解题时,要抓住几何图形自身的特点,如等腰(边)三角形的三线合一、中位线定理、菱形的对角线互相垂直等.还可以通过解三角形,产生一些题目所需要的条件,对于一些较复杂的问题,注意应用转化思想解决问题.
随堂检测
1.直线l⊥平面α,l 平面β,则α与β的位置关系是( )
A.平行 B.可能重合
C.相交且垂直 D.相交不垂直
C
直线l⊥平面α
l 平面β
α⊥β
2.从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是( )
A.互为余角 B.相等
C.其和为周角 D.互为补角
D
3.已知l⊥平面α,直线m 平面β.有下面四个命题:
①α∥β l⊥m;②α⊥β l∥m;③l∥m α⊥β;④l⊥m α∥β.
其中正确的两个命题是( )
A.①② B.③④
C.②④ D.①③
∵l⊥α,α∥β,∴l⊥β,∵m β,∴l⊥m,故①正确;
D
∵l∥m,l⊥α,∴m⊥α,又∵m β,∴α⊥β,故③正确.
4.在正方体ABCD- A1B1C1D1中,二面角A -BC- A1的平面角等于_________.
45°
本课小结
1.求二面角大小的步骤
简称为“一作、二证、三求”.
2.平面与平面垂直的判定定理的应用思路
(1)本质:通过直线与平面垂直来证明平面与平面垂直,即线面垂直 面面垂直.
(2)证题思路:处理面面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题来解决.
3.面面垂直的性质定理揭示了“面面垂直、线面垂直及线线垂直”间的内在联系,体现了数学中的化归转化思想,其转化关系如下:
平面与平面垂直
本节目标
学 习 目 标 核 心 素 养
1.理解二面角的有关概念,会作二面角的平面角,能求简单二面角平面角的大小.(难点、易错点) 2.了解面面垂直的定义,掌握面面垂直的判定定理和性质定理,初步学会用定理证明垂直关系.(重点) 3.熟悉线线垂直、线面垂直的转化.(重点) 1. 通过学习面面垂直的判定定理和性质定理,提升直观想象、逻辑推理的数学素养.
2. 通过学习二面角,提升直观想象、逻辑推理、数学运算的数学素养.
课前预习
预习课本P155~161,思考并完成以下问题
1.什么叫做二面角?什么叫做二面角的平面角?
2.两个平面互相垂直是怎样定义的?两个平面互相垂直的判定定理是什么?
3.平面与平面垂直的性质定理是什么?
课前小测
1.如图所示的二面角可记为( )
A.α- β- l B.M -l -N C.l -M- N D.l- β -α
B
√
2.已知直线l⊥平面α,则经过l且和α垂直的平面( )
A.有一个 B.有两个
C.有无数个 D.不存在
C
经过l的任一平面都和α垂直
3.平面α⊥平面β,直线l α,直线m β,则直线l,m的位置关系是_________________.
α
β
相交
α
β
平行
α
β
异面
相交、平行或异面
4.如图所示,三棱锥P -ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B- PA- C的大小等于_______.
PA⊥平面ABC
PA⊥AB,PA⊥AC
∠BAC为B -PA- C的平面角
∠BAC=90°
所求二面角的大小为90°
90°
考点精讲
一、二面角的概念
1. 定 义
从一条直线出发的____________所组成的图形.
①这条直线叫做二面角的____,
②两个半平面叫做__________.
2.相关概念
两个半平面
棱
二面角的面
3. 画 法
4. 记 法
二面角α- l -β或α -AB- β或P- l -Q或P -AB -Q.
5. 二面角的平面角
若有 ①O ___ l;②OA ___α,OB ___β;③OA____ l,OB ____ l,
则二面角α- l- β的平面角是_______.
∈
⊥
⊥
∠AOB
6. 直二面角
平面角是直角的二面角叫做__________,二面角的平面角α的取值范围是____________.
直二面角
0°≤α≤180°
思考1:二面角的平面角的大小,是否与角的顶点在棱上的位置有关?
提示: 无关.如图,根据等角定理可知,∠AOB=∠A′O′B′,即二面角的平面角的大小与角的顶点的位置无关,只与二面角的大小有关.
二、平面与平面垂直
1. 定 义
3. 画 法
4. 记 作
一般地,两个平面相交,如果它们所成的二面角是___________,就说这两个平面互相垂直.
直二面角
α⊥β
4.判定定理
文字语言 如果一个平面过另一个平面的______,那么这两个平面垂直
图形语言
符号语言 l⊥α,_______ α⊥β
垂线
l β
思考2:两个平面垂直,则一个平面内的任何一条直线都垂直于另一个平面吗?
提示:不一定,只有在一个平面内垂直于交线的直线才垂直于另一个平面.
三.平面与平面垂直的性质定理
文字语言 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的_______,那么这条直线与另一个平面________.
符号语言 a⊥β
图形语言
作用 ①面面垂直 ________垂直
②作面的垂线
交线
垂直
线面
思考3:如果α⊥β,则α内的直线必垂直于β内的无数条直线吗?
提示:正确.若设α∩β=l,a α,b β,b⊥l,则a⊥b,故β内与b平行的无数条直线均垂直于α内的任意直线.
题型一 二面角的计算问题
典例剖析
【例1】如图,已知三棱锥A -BCD的各棱长均为2,求二面角A -CD- B的余弦值.
M
H
如图,取CD的中点M,连接AM,BM,则AM⊥CD,BM⊥CD.
由二面角的定义可知∠AMB为二面角A CD B的平面角.
方法技巧
1
2
3
1.求二面角大小的步骤
找出这个平面角;
证明这个角是二面角的平面角;
作出这个角所在的三角形,解这个三角形,求出角的大小.
2.确定二面角的平面角的方法
过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角,如图所示.
定义法
在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.
垂面法
活学活用
1.如图,AC⊥平面BCD,BD⊥CD, AC= AD,求平面 ABD 与平面BCD 所成的二面角的大小.
因为AC⊥平面 BCD,BD 平面 BCD,所以BD⊥AC.
又因为BD⊥CD,AC∩CD=C,
所以BD⊥平面 ACD.
因为AD 平面 ACD,所以AD⊥BD,
所以∠ADC即为平面 ABD 与平面 BCD 所成二面角的平面角.
在Rt△ACD中,AC= AD,所以∠ADC=30°.
题型二 平面与平面垂直的判定
【例2】 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC. 求证:平面ABC⊥平面SBC.
∠BSA=∠CSA=60°,SA=SB=SC,所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.取BC的中点D,如图所示,
连接AD,SD,则AD⊥BC,SD⊥BC,所以∠ADS为二面角A -BC- S的平面角.
在Rt△BSC中,因为SB=SC=a,所以SD= a,BD= a.
在Rt△ABD中,AD= a,在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A -BC -S为直二面角,故平面ABC⊥平面SBC.
法一
【例2】 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC. 求证:平面ABC⊥平面SBC.
法二
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
因为△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又因为AD 平面ABC,所以平面ABC⊥平面SBC.
方法技巧
证明面面垂直常用的方法
两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
定义法
即说明两个半平面所成的二面角是直二面角
判定定理法
在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为线面垂直;
性质法
活学活用
2.如图所示,四边形ABCD是边长为a的菱形,PC⊥平面ABCD,E是PA的中点,求证:平面BDE⊥平面ABCD.
连接AC,设AC∩BD=O,连接OE.
因为O为AC中点,E为PA的中点,
所以EO是△PAC的中位线,
所以EO∥PC.
因为PC⊥平面ABCD,所以EO⊥平面ABCD.
又因为EO 平面BDE,
所以平面BDE⊥平面ABCD.
题型三 面面垂直性质定理的应用
【例3】如图,在三棱锥P -ABC中,PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥AB.
如图,在平面PAB内,作AD⊥PB于点D.
平面PAB⊥平面PBC
平面PAB∩平面PBC=PB
AD 平面PAB
AD⊥PB
AD⊥平面PBC
BC 平面PBC
AD⊥BC
PA⊥平面ABC,BC 平面ABC
PA⊥BC
PA∩AD=A
BC⊥平面PAB
AB 平面PAB
BC⊥AB
方法技巧
(1) 线面垂直的判定定理;
(2) 面面垂直的性质定理;
(3) 若a∥b,a⊥α,则b⊥α (a、b为直线,α为平面);
(4) 若a⊥α,α∥β,则a⊥β (a为直线,α,β为平面);
证明或判定线面垂直的常用方法
∵平面VAB⊥平面ABCD,且BC⊥AB,平面VAB∩平面ABCD=AB,BC 平面ABCD.
∴BC⊥平面VAB,
又VA 平面VAB,∴BC⊥VA,
又VB⊥平面VAD,∴VB⊥VA,
又VB∩BC=B,∴VA⊥平面VBC,
∵VA 平面VAC,∴平面VBC⊥平面VAC.
活学活用
3.如图,四棱锥V- ABCD的底面是矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD. 求证:平面VBC⊥平面VAC.
难点突破
[探究问题]
试总结线线垂直、线面垂直、面面垂直之间的转化关系.
[提示] 垂直问题转化关系如下所示:
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:(1)DE=DA;
设BD=a,如图,作DF∥BC交CE于F,
则CF=DB=a.因为CE⊥平面ABC,
所以BC⊥CF,DF⊥EC,
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(2)平面BDM⊥平面ECA;
取CA的中点N,连接MN,BN,则
所以四边形MNBD为平行四边形,所以MD∥BN.
又因为EC⊥平面ABC,所以EC⊥BN,EC⊥MD.
又DE=DA,M为EA的中点,所以DM⊥AE.
所以DM⊥平面AEC,所以平面BDM⊥平面ECA.
【例4】 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(3)平面DEA⊥平面ECA.
由(2)知DM⊥平面AEC,而DM 平面DEA,
所以平面DEA⊥平面ECA.
活学活用
4、本例条件不变,试求平面ADE与平面ABC所成二面角的大小.
如图延长ED交CB延长线于点N,连接AN,设BD=a,由例题知,CE=AC=BC=AB=2a,
在△CEN中,由知B为CN中点,∴CB=BN=2a.
∴△ABN中,∠ABN=120°,∠BAN=∠BNA=30°,
∴∠CAN=90°,即NA⊥CA.
又EC⊥平面ABC,∴EC⊥NA,又CA∩CE=C,
∴NA⊥平面ACE,∴NA⊥AE,NA⊥AC,且AN为平面ADE与平面ABC的交线.
∴∠CAE为平面ADE与平面ABC所成二面角的平面角,
在Rt△ACE中,AC=CE,∴∠CAE=45°.
所以平面ADE与平面ABC所成二面角为45°.
方法技巧
垂直关系的互化及解题策略
空间问题化成平面问题是解决立体几何问题的一个基本原则,解题时,要抓住几何图形自身的特点,如等腰(边)三角形的三线合一、中位线定理、菱形的对角线互相垂直等.还可以通过解三角形,产生一些题目所需要的条件,对于一些较复杂的问题,注意应用转化思想解决问题.
随堂检测
1.直线l⊥平面α,l 平面β,则α与β的位置关系是( )
A.平行 B.可能重合
C.相交且垂直 D.相交不垂直
C
直线l⊥平面α
l 平面β
α⊥β
2.从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是( )
A.互为余角 B.相等
C.其和为周角 D.互为补角
D
3.已知l⊥平面α,直线m 平面β.有下面四个命题:
①α∥β l⊥m;②α⊥β l∥m;③l∥m α⊥β;④l⊥m α∥β.
其中正确的两个命题是( )
A.①② B.③④
C.②④ D.①③
∵l⊥α,α∥β,∴l⊥β,∵m β,∴l⊥m,故①正确;
D
∵l∥m,l⊥α,∴m⊥α,又∵m β,∴α⊥β,故③正确.
4.在正方体ABCD- A1B1C1D1中,二面角A -BC- A1的平面角等于_________.
45°
本课小结
1.求二面角大小的步骤
简称为“一作、二证、三求”.
2.平面与平面垂直的判定定理的应用思路
(1)本质:通过直线与平面垂直来证明平面与平面垂直,即线面垂直 面面垂直.
(2)证题思路:处理面面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题来解决.
3.面面垂直的性质定理揭示了“面面垂直、线面垂直及线线垂直”间的内在联系,体现了数学中的化归转化思想,其转化关系如下:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
