人教A版(2019)数学必修第二册10_3_1频率的稳定性课件(共31张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第二册10_3_1频率的稳定性课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 872.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 13:39:15 | ||
图片预览











文档简介
(共31张PPT)
频率的稳定性
本节目标
学 习 目 标 核 心 素 养
1.理解频率的稳定性. 2.结合实例,会用频率估计概率. 1.通过对频率和概率联系和区别的学习,培养学生数学抽象素养.
2.通过利用随机事件的频率估计其概率,培养学生数学运算素养.
重难点
课前预习
预习课本P251~254,思考并完成以下问题
(1) 频率具有什么性质?
(2) 频率稳定性有什么作用?
预习检测
1.某人将一枚硬币连掷10次,正面朝上的情况出现了8次,若用A表示“正面朝上”这一事件,则A的( )
A.概率为 B.频率为
C.频率为8 D.概率接近于8
B
做n次随机试验,事件A发生了m次,则事件A发生的频率为.如果多次进行试验,事件A发生的频率总在某个常数附近摆动,那么这个常数才是事件A的概率.故为事件A的频率.
2.每道选择题有4个选项,其中只有1个选项是正确的,某次考试共12道选择题,某同学说:“每个选项正确的概率是,若每题都选择第一个选项,则一定有3道题的选择结果正确”.这句话( )
A.正确 B.错误
C.有一定道理 D.无法解释
B
×
3.经过市场抽检,质检部门得知市场上食用油合格率为80%,经调查,某市市场上的食用油大约有80个品牌,则不合格的食用油品牌大约有( )
A.64个 B.640个 C.16个 D.160个
80×(1-80%)=80×20%=16个
C
考点精讲
1.频率的稳定性
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐_________事件A发生的概率P(A),我们称频率的这个性质为频率的稳定性.
稳定于
2.频率稳定性的作用
可以用频率fn(A)估计概率P(A)
思考:频率和概率有什么区别和联系?
对于给定的随机事件A,由于事件A发生的频率fn(A)随着试验次数的增加稳定于概率P(A),因此可以用频率fn(A)来估计概率P(A).
(1)在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例fn(A)= 为事件A出现的频率.
(2)概率是度量随机事件发生的可能性大小的量.
(3)频率是一个变量,随着试验次数的变化而变化,概率是一个定值,是某事件的固有属性.
区别
联系
题型一 频率和概率的区别和联系
典例剖析
【例1】下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
×
×
×
√
方法技巧
理解概率与频率应关注的三个方面
(1)概率是随机事件发生可能性大小的度量,是随机事件A的本质属性,随机事件A发生的概率是大量重复试验中事件A发生的频率的近似值.
(2)由频率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
活学活用
1.“某彩票的中奖概率为”意味着( )
A.买100张彩票就一定能中奖
B.买100张彩票能中一次奖
C.买100张彩票一次奖也不中
D.购买彩票中奖的可能性为
D
√
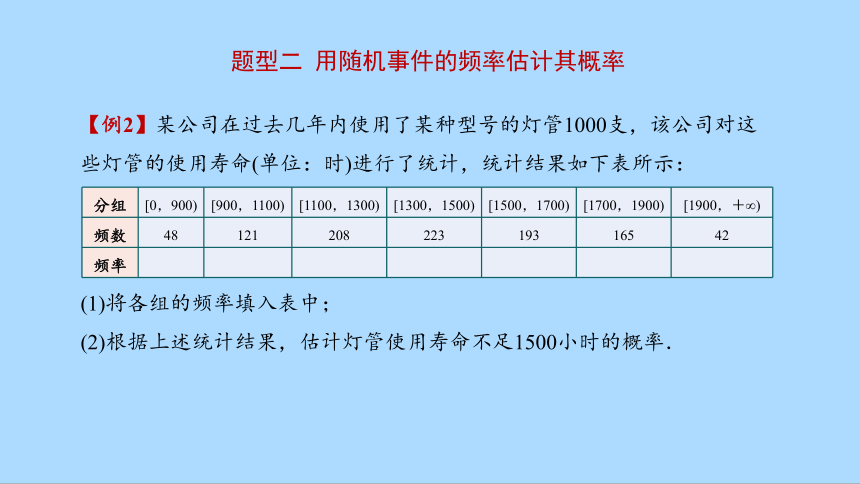
题型二 用随机事件的频率估计其概率
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计灯管使用寿命不足1500小时的概率.
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(1)将各组的频率填入表中;
0.048
0.121
0.208
0.223
0.193
0.165
0.042
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(2)根据上述统计结果,估计灯管使用寿命不足1500小时的概率.
0.048
0.121
0.208
0.223
0.193
0.165
0.042
样本中使用寿命不足1500小时的频数是48+121+208+223=600.
所以样本中使用寿命不足1500小时的频率是=0.6,
即灯管使用寿命不足1500小时的概率约为0.6.
方法技巧
1.频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率,频率本身是随机变量,当n很大时,频率总是在一个稳定值附近摆动,这个稳定值就是概率.
2.解此类题目的步骤:先利用频率的计算公式依次计算频率,然后用频率估计概率.
活学活用
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(1)若每辆车的投保金额为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(1)若每辆车的投保金额为2800元,估计赔付金额大于投保金额的概率;
设A表示事件“赔付金额为3000元”,B表示事件“赔付金额为4000元”,以频率估计概率得P(A)= =0.15,P(B)= =0.12,
由于投保额为2800元,赔付金额大于投保金额的情形是赔付3000元和4000元,A与B互斥,所以所求概率为P(A)+P(B)=0.15+0.12=0.27.
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主是新司机的有0.1×1000=100(位),而赔付金额为4000元的车辆中车主为新司机的有0.2×120=24(位),
所以样本车辆中新司机车主获赔金额为4000元的频率为=0.24,
由频率估计概率得P(C)=0.24.
题型三 游戏的公平性
1.判断某种游戏规则是否公平的标准是什么?
[提示]
如果参加比赛的双方获胜(或失败)的概率是一样的,那么就说明这个游戏规则是公平的;否则就是不公平的.
[探究问题]
[提示]
[探究问题]
2.小明和小红通过抓阄决定谁代表班级参加学校举行的演讲比赛,规则如下:在一个不透明的盒子里有三个质地完全相同的小卡片,上面分别写有“参加”“不参加”“谢谢参与”,小明和小红分别从中摸取一个小卡片,摸到“参加”者代表班级参加学校举行的演讲比赛.这个游戏规则公平吗?请说明理由.
公平.因为每个人摸到“参加”的概率都是.
【例3】 某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
和 4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
由表可知该游戏可能出现的情况共有12种,其中两数字之和为偶数的有6种,为奇数的也有6种,所以(1)班代表获胜的概率P1= = ,(2)班代表获胜的概率P2== ,即P1=P2,机会是均等的,所以该方案对双方是公平的.
活学活用
3.在例3中,若把游戏规则改为:两人各自转动转盘一次,转盘停止后,两个指针指向的两个数字相乘,如果是偶数,那么(1)班代表获胜,否则(2)班代表获胜.游戏规则公平吗?为什么?
不公平.
因为乘积出现奇数的概率为= ,而出现偶数的概率为= .
和 4 5 6 7
1 4 5 6 7
2 8 10 12 14
3 12 15 18 21
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
为了尽可能获胜,乙应选择方案B.猜“不是4的整数倍”.
因为“不是4的整数倍”的概率为=0.8,超过了0.5.
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
为了保证游戏的公平性,应当选择方案A,这是因为方案A是猜“是奇数”和“是偶数”的概率均为0.5,从而保证了该游戏的公平性.
方法技巧
游戏公平性的标准及判断方法
(1)游戏规则是否公平,要看对游戏的双方来说,获胜的可能性或概率是否相同.若相同,则规则公平,否则就是不公平的.
(2)具体判断时,可以求出按所给规则双方的获胜概率,再进行比较.
随堂检测
(1)随机事件的频率和概率不可能相等.( )
(2)随机事件的频率和概率都随着试验次数的变化而变化.( )
(3)概率能反映随机事件发生可能性的大小,而频率则不能.( )
频率和概率都能反映随机事件发生的可能性的大小
×
二者可能相等
概率是不变的,是客观存在的
×
×
1.判断正误
2.给出下列3种说法:
①设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品;
②做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是;
③随机事件发生的频率就是这个随机事件发生的概率.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
A
3.设某厂产品的次品率为2%,估算该厂8000件产品中合格品的件数可能为( )
A.160 B.7840
C.7998 D.7800
B
次品率为2%,故次品约8000×2%=160(件),故合格品的件数可能为7840.
(1)某商场为促进销售,举办有奖销售活动,凡购买其商品的顾客中奖的概率为0.20;
(2)一生产厂家称,我们厂生产的产品合格的概率是0.98.
4.试解释下面情况中概率的意义:
是说该厂生产的产品合格的可能性是98%.
指购买其商品的顾客中奖的可能性是20%.
本课小结
1.概率与频率的区别
频率是一个变量,随着试验次数的变化而变化,概率是一个定值,是某事件的固有属性.
2.概率与频率的关系
对于一个事件而言,概率是一个常数,频率则随试验次数的变化而变化,次数越多频率越接近其概率,因此可以用随机事件的频率来估计其概率.
频率的稳定性
本节目标
学 习 目 标 核 心 素 养
1.理解频率的稳定性. 2.结合实例,会用频率估计概率. 1.通过对频率和概率联系和区别的学习,培养学生数学抽象素养.
2.通过利用随机事件的频率估计其概率,培养学生数学运算素养.
重难点
课前预习
预习课本P251~254,思考并完成以下问题
(1) 频率具有什么性质?
(2) 频率稳定性有什么作用?
预习检测
1.某人将一枚硬币连掷10次,正面朝上的情况出现了8次,若用A表示“正面朝上”这一事件,则A的( )
A.概率为 B.频率为
C.频率为8 D.概率接近于8
B
做n次随机试验,事件A发生了m次,则事件A发生的频率为.如果多次进行试验,事件A发生的频率总在某个常数附近摆动,那么这个常数才是事件A的概率.故为事件A的频率.
2.每道选择题有4个选项,其中只有1个选项是正确的,某次考试共12道选择题,某同学说:“每个选项正确的概率是,若每题都选择第一个选项,则一定有3道题的选择结果正确”.这句话( )
A.正确 B.错误
C.有一定道理 D.无法解释
B
×
3.经过市场抽检,质检部门得知市场上食用油合格率为80%,经调查,某市市场上的食用油大约有80个品牌,则不合格的食用油品牌大约有( )
A.64个 B.640个 C.16个 D.160个
80×(1-80%)=80×20%=16个
C
考点精讲
1.频率的稳定性
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐_________事件A发生的概率P(A),我们称频率的这个性质为频率的稳定性.
稳定于
2.频率稳定性的作用
可以用频率fn(A)估计概率P(A)
思考:频率和概率有什么区别和联系?
对于给定的随机事件A,由于事件A发生的频率fn(A)随着试验次数的增加稳定于概率P(A),因此可以用频率fn(A)来估计概率P(A).
(1)在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例fn(A)= 为事件A出现的频率.
(2)概率是度量随机事件发生的可能性大小的量.
(3)频率是一个变量,随着试验次数的变化而变化,概率是一个定值,是某事件的固有属性.
区别
联系
题型一 频率和概率的区别和联系
典例剖析
【例1】下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
×
×
×
√
方法技巧
理解概率与频率应关注的三个方面
(1)概率是随机事件发生可能性大小的度量,是随机事件A的本质属性,随机事件A发生的概率是大量重复试验中事件A发生的频率的近似值.
(2)由频率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
活学活用
1.“某彩票的中奖概率为”意味着( )
A.买100张彩票就一定能中奖
B.买100张彩票能中一次奖
C.买100张彩票一次奖也不中
D.购买彩票中奖的可能性为
D
√
题型二 用随机事件的频率估计其概率
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计灯管使用寿命不足1500小时的概率.
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(1)将各组的频率填入表中;
0.048
0.121
0.208
0.223
0.193
0.165
0.042
【例2】某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:
分组 [0,900) [900,1100) [1100,1300) [1300,1500) [1500,1700) [1700,1900) [1900,+∞)
频数 48 121 208 223 193 165 42
频率
(2)根据上述统计结果,估计灯管使用寿命不足1500小时的概率.
0.048
0.121
0.208
0.223
0.193
0.165
0.042
样本中使用寿命不足1500小时的频数是48+121+208+223=600.
所以样本中使用寿命不足1500小时的频率是=0.6,
即灯管使用寿命不足1500小时的概率约为0.6.
方法技巧
1.频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率,频率本身是随机变量,当n很大时,频率总是在一个稳定值附近摆动,这个稳定值就是概率.
2.解此类题目的步骤:先利用频率的计算公式依次计算频率,然后用频率估计概率.
活学活用
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(1)若每辆车的投保金额为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(1)若每辆车的投保金额为2800元,估计赔付金额大于投保金额的概率;
设A表示事件“赔付金额为3000元”,B表示事件“赔付金额为4000元”,以频率估计概率得P(A)= =0.15,P(B)= =0.12,
由于投保额为2800元,赔付金额大于投保金额的情形是赔付3000元和4000元,A与B互斥,所以所求概率为P(A)+P(B)=0.15+0.12=0.27.
2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔偿金额(元) 0 1000 2000 3000 4000
车辆数(辆) 500 130 100 150 120
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主是新司机的有0.1×1000=100(位),而赔付金额为4000元的车辆中车主为新司机的有0.2×120=24(位),
所以样本车辆中新司机车主获赔金额为4000元的频率为=0.24,
由频率估计概率得P(C)=0.24.
题型三 游戏的公平性
1.判断某种游戏规则是否公平的标准是什么?
[提示]
如果参加比赛的双方获胜(或失败)的概率是一样的,那么就说明这个游戏规则是公平的;否则就是不公平的.
[探究问题]
[提示]
[探究问题]
2.小明和小红通过抓阄决定谁代表班级参加学校举行的演讲比赛,规则如下:在一个不透明的盒子里有三个质地完全相同的小卡片,上面分别写有“参加”“不参加”“谢谢参与”,小明和小红分别从中摸取一个小卡片,摸到“参加”者代表班级参加学校举行的演讲比赛.这个游戏规则公平吗?请说明理由.
公平.因为每个人摸到“参加”的概率都是.
【例3】 某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
和 4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
由表可知该游戏可能出现的情况共有12种,其中两数字之和为偶数的有6种,为奇数的也有6种,所以(1)班代表获胜的概率P1= = ,(2)班代表获胜的概率P2== ,即P1=P2,机会是均等的,所以该方案对双方是公平的.
活学活用
3.在例3中,若把游戏规则改为:两人各自转动转盘一次,转盘停止后,两个指针指向的两个数字相乘,如果是偶数,那么(1)班代表获胜,否则(2)班代表获胜.游戏规则公平吗?为什么?
不公平.
因为乘积出现奇数的概率为= ,而出现偶数的概率为= .
和 4 5 6 7
1 4 5 6 7
2 8 10 12 14
3 12 15 18 21
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
为了尽可能获胜,乙应选择方案B.猜“不是4的整数倍”.
因为“不是4的整数倍”的概率为=0.8,超过了0.5.
4.若在例3中,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的数字相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“不是4的整数倍数”.
请回答下列问题:
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
为了保证游戏的公平性,应当选择方案A,这是因为方案A是猜“是奇数”和“是偶数”的概率均为0.5,从而保证了该游戏的公平性.
方法技巧
游戏公平性的标准及判断方法
(1)游戏规则是否公平,要看对游戏的双方来说,获胜的可能性或概率是否相同.若相同,则规则公平,否则就是不公平的.
(2)具体判断时,可以求出按所给规则双方的获胜概率,再进行比较.
随堂检测
(1)随机事件的频率和概率不可能相等.( )
(2)随机事件的频率和概率都随着试验次数的变化而变化.( )
(3)概率能反映随机事件发生可能性的大小,而频率则不能.( )
频率和概率都能反映随机事件发生的可能性的大小
×
二者可能相等
概率是不变的,是客观存在的
×
×
1.判断正误
2.给出下列3种说法:
①设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品;
②做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是;
③随机事件发生的频率就是这个随机事件发生的概率.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
A
3.设某厂产品的次品率为2%,估算该厂8000件产品中合格品的件数可能为( )
A.160 B.7840
C.7998 D.7800
B
次品率为2%,故次品约8000×2%=160(件),故合格品的件数可能为7840.
(1)某商场为促进销售,举办有奖销售活动,凡购买其商品的顾客中奖的概率为0.20;
(2)一生产厂家称,我们厂生产的产品合格的概率是0.98.
4.试解释下面情况中概率的意义:
是说该厂生产的产品合格的可能性是98%.
指购买其商品的顾客中奖的可能性是20%.
本课小结
1.概率与频率的区别
频率是一个变量,随着试验次数的变化而变化,概率是一个定值,是某事件的固有属性.
2.概率与频率的关系
对于一个事件而言,概率是一个常数,频率则随试验次数的变化而变化,次数越多频率越接近其概率,因此可以用随机事件的频率来估计其概率.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
