19.7直角三角形全等的判定 精品教学课件(共25张PPT)
文档属性
| 名称 | 19.7直角三角形全等的判定 精品教学课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 684.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
19.7直角三角形全等的判定
第 19 章 几何证明
八年级上册数学沪教版
学习目标
1.通过探索判定两个直角三角形全等的特殊的方法,体会特殊与一般的关系,掌握“H.L”这一判定两个直角三角形全等的特殊方法.
2.会利用“H.L”判定方法和一般三角形全等的方法判定直角三角形全等.
3.在探索判定两个直角三角形全等的特殊的方法的过程中体验转化的思想.
如图,若要判定△ABC和△DEF全等,可以添加哪些全等条件?分别运用了哪条判定定理?
回顾:一般的三角形有哪些判定全等的方法
复习引入
角边角(A.S.A)
边角边(S.A.S)
角角边(A.A.S)
边边边(S.S.S)
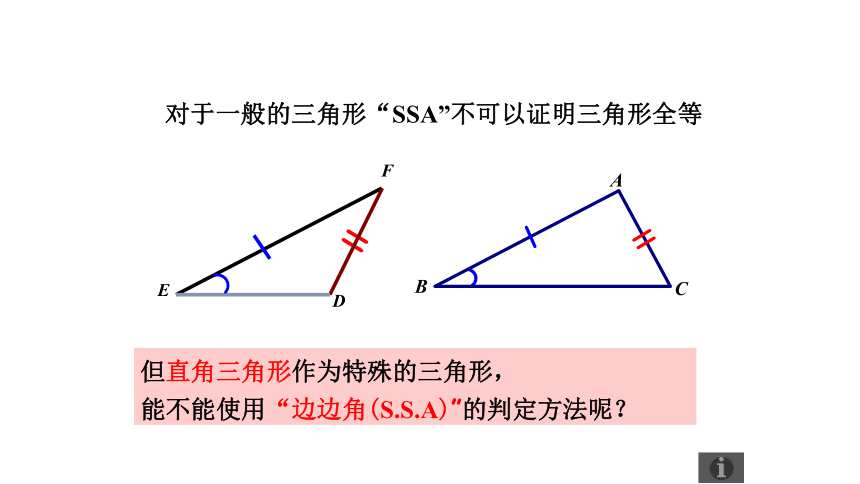
对于一般的三角形“SSA”不可以证明三角形全等
F
E
D
但直角三角形作为特殊的三角形,
能不能使用“边边角(S.S.A)”的判定方法呢?
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’= 90o ,AC=A’C’,AB=A’B’
求证: Rt△ABC ≌Rt△A’B’C’
A’
C’
B’
A
B
C
A’
C’
B’
A
B
C
关键 能够从已知条件中得到一个锐角对应相等。
证明 如图所示,把△ABC和△A’B’C’拼在一起,由于AC=A’C’,因此可使AC和A’C’重合,由于 ∠ACB=∠A’C’B’=90o,因此点B、C、B’在一条直线上,于是得到了△ABB’。
A’
C’
B’
A’
C’
B’
A’
C’
B’
(A’)
(C’)
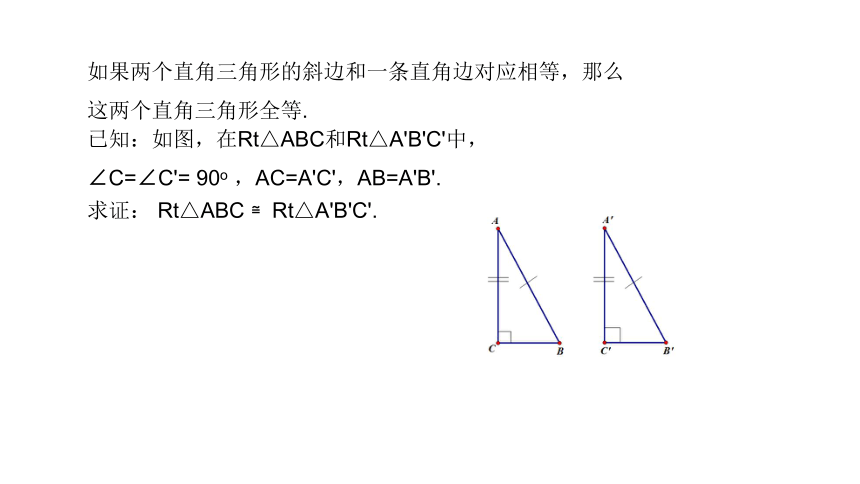
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.
已知:如图,在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'= 90o ,AC=A'C',AB=A'B'.
求证: Rt△ABC ≌Rt△A'B'C'.
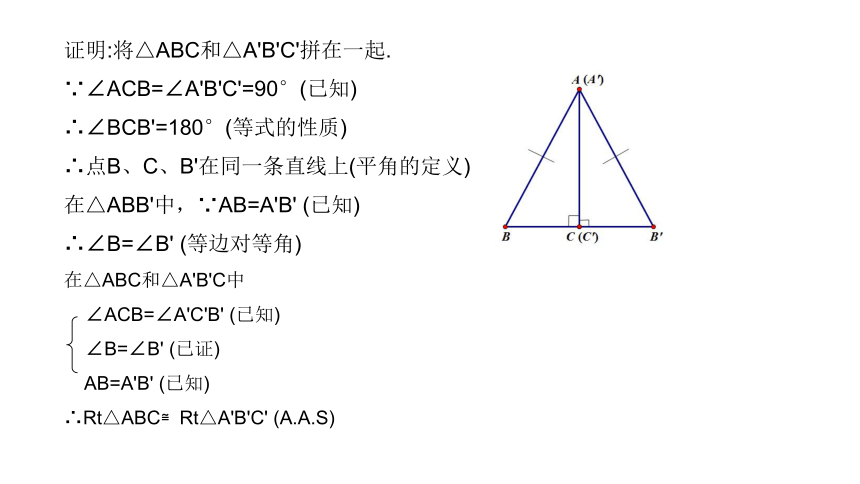
证明:将△ABC和△A'B'C'拼在一起.
∵∠ACB=∠A'B'C'=90°(已知)
∴∠BCB'=180°(等式的性质)
∴点B、C、B'在同一条直线上(平角的定义)
在△ABB'中,∵AB=A'B' (已知)
∴∠B=∠B' (等边对等角)
在△ABC和△A'B'C中
∠ACB=∠A'C'B' (已知)
∠B=∠B' (已证)
AB=A'B' (已知)
∴Rt△ABC≌Rt△A'B'C' (A.A.S)
定理 如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC和Rt△A’B’C’中
AC=A’C’,
AB=A’B’
∴Rt△ABC ≌Rt△A’B’C’(H.L.)
(H.L.)
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”定理
或“HL”
前提
条件1
条件2
直角三角形全等的条件
概念辨析:有两边对应相等的两个直角三角形一定全等吗?
情况1:全等
情况2:全等
(SAS)
( HL)
情况3:不全等
练一练
如图,如图,把下列说明Rt△ABC≌Rt△DEF的条件或依据补充完整。(口答)
⑴_________∠A=∠D(A.S.A)
⑵AC=DF,_________(S.A.S)
⑶BC=EF,AB=DE(_____)
⑷AC=DF,_________(H.L)
⑸∠A=∠D,BC=EF(_____)
⑹_________,AC=DF(A.A.S)
AC=DF
BC=EF
H.L
AB=DE
A.A.S
∠B=∠E
适时小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
斜边,直角边
和直角
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
例1已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
B
C
E
B
C
D
∠ABC=∠ACB
AB=AC?
∟
∟
证明:
∵CE⊥AB,BD⊥AC
(已知),
∴△EBC和△DCB都是直角三角形.
在Rt△EBC与Rt△DCB中,
CE=BD (已知),
BC=CB (公共边),
∴Rt△EBC≌Rt△DCB
(H.L).
∴∠EBC=∠DCB
(全等…角相等).
∴AB=AC
(等角对等边).
即△ABC是等腰三角形.
(直角三角形的意义),
BACK
AB=AC?
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
A
B
D
A
C
E
∟
∟
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
B
C
E
B
C
D
A
B
D
A
C
E
∟
∟
法一
(A.A.S)
∟
∟
法二
(H.L)
例2.求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
过点O、Q,作射线OQ.
∵QD⊥OA,QE⊥OB
(已知),
∴△QDO和△QEO都是直角三角形
(直角三角形的意义).
在Rt△QDO与Rt△QEO中,
QD=
QE
OQ=
(公共边),
∴Rt△QDO≌Rt△QEO
(H.L).
(已知),
OQ
例2.求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∴Rt△QDO≌Rt△QEO
(H.L)
∴∠1=∠2
(全等三角形的对应角相等)
∴OQ是∠AOB的平分线
(角平分线的意义)
即点Q在∠AOB的平分线上.
过点O、Q,作射线OQ
课本练习
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:(1) DE=DF (2) EB=FC.
A
B
E
F
C
D
证明:
∵AD是∠BAC的平分线,
DE⊥AB, DF⊥AC (已知),
∴DE=DF
(在角的平分线上的点到这个角的两边的距离相等).
△BDE和△CDF都是直角三角形.
在Rt△BDE和Rt △CDF中,
BD=CD(已知),
DE=DF (已证),
∴Rt△BDE≌Rt△CDF(H.L).
∴EB=FC(全等三角形的对应边相等).
F
A
D
E
B
C
∟
∟
2.已知:如图,EC⊥AB,FD⊥AB,垂足分别为点C、D,AF=BE,FD=EC
求证:AC=BD
课堂小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
运用“HL”定理时,
前提条件必须是___________,
然后依据_______和____________对应相等,
再证明两个直角三角形全等.
直角三角形
斜边
一条直角边
THANKS
“
”
19.7直角三角形全等的判定
第 19 章 几何证明
八年级上册数学沪教版
学习目标
1.通过探索判定两个直角三角形全等的特殊的方法,体会特殊与一般的关系,掌握“H.L”这一判定两个直角三角形全等的特殊方法.
2.会利用“H.L”判定方法和一般三角形全等的方法判定直角三角形全等.
3.在探索判定两个直角三角形全等的特殊的方法的过程中体验转化的思想.
如图,若要判定△ABC和△DEF全等,可以添加哪些全等条件?分别运用了哪条判定定理?
回顾:一般的三角形有哪些判定全等的方法
复习引入
角边角(A.S.A)
边角边(S.A.S)
角角边(A.A.S)
边边边(S.S.S)
对于一般的三角形“SSA”不可以证明三角形全等
F
E
D
但直角三角形作为特殊的三角形,
能不能使用“边边角(S.S.A)”的判定方法呢?
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’= 90o ,AC=A’C’,AB=A’B’
求证: Rt△ABC ≌Rt△A’B’C’
A’
C’
B’
A
B
C
A’
C’
B’
A
B
C
关键 能够从已知条件中得到一个锐角对应相等。
证明 如图所示,把△ABC和△A’B’C’拼在一起,由于AC=A’C’,因此可使AC和A’C’重合,由于 ∠ACB=∠A’C’B’=90o,因此点B、C、B’在一条直线上,于是得到了△ABB’。
A’
C’
B’
A’
C’
B’
A’
C’
B’
(A’)
(C’)
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.
已知:如图,在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'= 90o ,AC=A'C',AB=A'B'.
求证: Rt△ABC ≌Rt△A'B'C'.
证明:将△ABC和△A'B'C'拼在一起.
∵∠ACB=∠A'B'C'=90°(已知)
∴∠BCB'=180°(等式的性质)
∴点B、C、B'在同一条直线上(平角的定义)
在△ABB'中,∵AB=A'B' (已知)
∴∠B=∠B' (等边对等角)
在△ABC和△A'B'C中
∠ACB=∠A'C'B' (已知)
∠B=∠B' (已证)
AB=A'B' (已知)
∴Rt△ABC≌Rt△A'B'C' (A.A.S)
定理 如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC和Rt△A’B’C’中
AC=A’C’,
AB=A’B’
∴Rt△ABC ≌Rt△A’B’C’(H.L.)
(H.L.)
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”定理
或“HL”
前提
条件1
条件2
直角三角形全等的条件
概念辨析:有两边对应相等的两个直角三角形一定全等吗?
情况1:全等
情况2:全等
(SAS)
( HL)
情况3:不全等
练一练
如图,如图,把下列说明Rt△ABC≌Rt△DEF的条件或依据补充完整。(口答)
⑴_________∠A=∠D(A.S.A)
⑵AC=DF,_________(S.A.S)
⑶BC=EF,AB=DE(_____)
⑷AC=DF,_________(H.L)
⑸∠A=∠D,BC=EF(_____)
⑹_________,AC=DF(A.A.S)
AC=DF
BC=EF
H.L
AB=DE
A.A.S
∠B=∠E
适时小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
斜边,直角边
和直角
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
例1已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
B
C
E
B
C
D
∠ABC=∠ACB
AB=AC?
∟
∟
证明:
∵CE⊥AB,BD⊥AC
(已知),
∴△EBC和△DCB都是直角三角形.
在Rt△EBC与Rt△DCB中,
CE=BD (已知),
BC=CB (公共边),
∴Rt△EBC≌Rt△DCB
(H.L).
∴∠EBC=∠DCB
(全等…角相等).
∴AB=AC
(等角对等边).
即△ABC是等腰三角形.
(直角三角形的意义),
BACK
AB=AC?
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
A
B
D
A
C
E
∟
∟
例1.已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
B
C
E
B
C
D
A
B
D
A
C
E
∟
∟
法一
(A.A.S)
∟
∟
法二
(H.L)
例2.求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
过点O、Q,作射线OQ.
∵QD⊥OA,QE⊥OB
(已知),
∴△QDO和△QEO都是直角三角形
(直角三角形的意义).
在Rt△QDO与Rt△QEO中,
QD=
QE
OQ=
(公共边),
∴Rt△QDO≌Rt△QEO
(H.L).
(已知),
OQ
例2.求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∴Rt△QDO≌Rt△QEO
(H.L)
∴∠1=∠2
(全等三角形的对应角相等)
∴OQ是∠AOB的平分线
(角平分线的意义)
即点Q在∠AOB的平分线上.
过点O、Q,作射线OQ
课本练习
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:(1) DE=DF (2) EB=FC.
A
B
E
F
C
D
证明:
∵AD是∠BAC的平分线,
DE⊥AB, DF⊥AC (已知),
∴DE=DF
(在角的平分线上的点到这个角的两边的距离相等).
△BDE和△CDF都是直角三角形.
在Rt△BDE和Rt △CDF中,
BD=CD(已知),
DE=DF (已证),
∴Rt△BDE≌Rt△CDF(H.L).
∴EB=FC(全等三角形的对应边相等).
F
A
D
E
B
C
∟
∟
2.已知:如图,EC⊥AB,FD⊥AB,垂足分别为点C、D,AF=BE,FD=EC
求证:AC=BD
课堂小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
运用“HL”定理时,
前提条件必须是___________,
然后依据_______和____________对应相等,
再证明两个直角三角形全等.
直角三角形
斜边
一条直角边
THANKS
“
”
