第二章 二次函数 专题小结 课件 (共34张PPT)
文档属性
| 名称 | 第二章 二次函数 专题小结 课件 (共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 18:41:07 | ||
图片预览











文档简介
(共34张PPT)
第二章 二次函数
专题小结
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
知识归纳
知识点1 二次函数的定义
知识点2 二次函数的图象与性质
知识点3 二次函数y=ax2+bx+c的图象特征与系数a,b,c的关系
知识点4 二次函数图象的平移
知识点5 二次函数解析式的求解
知识点6 二次函数与一元二次方程的关系
知识点7 二次函数的应用
知识点总结
知识点一、二次函数的定义
1.一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.特别地,当a≠0,b=c=0时,y=ax2是二次函数的特殊形式.
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中x1,x2是图象与x轴交点的横坐标.
二次函数 y=a(x-h)2+k y=ax2+bx+c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 a>0 开口向上
a < 0 开口向下
x=h
(h , k)
y最小=k
y最大=k
在对称轴左边,x↗ y↘;在对称轴右边, x↗ y↗
在对称轴左边,x↗ y↗;在对称轴右边, x↗ y↘
y最小=
y最大=
知识点二、二次函数的图象和性质
知识点三、二次函数y=ax2+bx+c的图象特征与系数a,b,c的关系
项目字母 字母的符号 图像的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
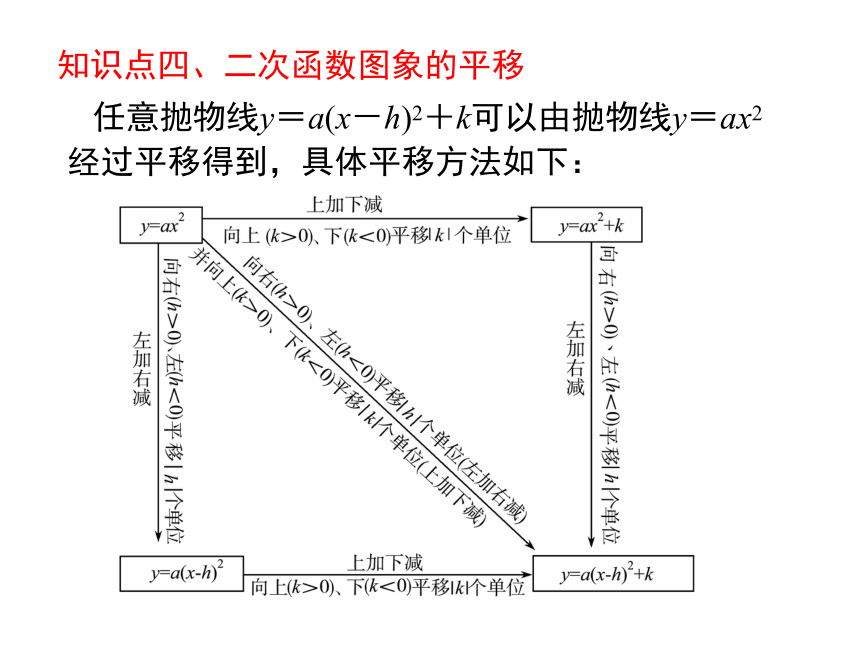
知识点四、二次函数图象的平移
任意抛物线y=a(x-h)2+k可以由抛物线y=ax2经过平移得到,具体平移方法如下:
知识点五、二次函数表达式的求法
1.一般式:y=ax2+bx+c (a≠ 0)
若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
2.顶点式:y=a(x-h)2+k(a≠0)
若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将解析式化为一般式.
3.交点式:y=a(x-x1)(x-x2)(a≠0)
若已知二次函数图象与x轴的两个交点的坐标,则设交点式y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a的值,最后将解析式化为一般式.
知识点六、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
知识点七、二次函数的应用
2.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
典例精析
1.函数y=3x2-1的图象与y轴的交点坐标是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
【答案】C
【分析】根据y轴上点的坐标特征,令x=0即可求解.
【详解】解:令x=0,则y=-1,
∴函数y=3x2-1的图象与y轴的交点坐标是(0,-1),
故选:C
典例精析
2.二次函数y1=3x2+bx+c与一次函数y2=kx+m的图象交于点A(2,3)和点B(4,1),要使y1>y2,则x的取值范围是( )
A.x<2 B.x<4
C.2<x<4 D.x<2或x>4
【答案】D
【详解】解:∵二次函数y1=3x2+bx+c与一次函数y2=kx+m的图象交于点A(2,3)和点B(4,1),
又∵二次函数y1=3x2+bx+c的图像开口向上,
∴要使y1>y2,则x的取值范围是:x<2或x>4,
故选D.
典例精析
3.若抛物线y=m开口向下,则m的值为( )
A.2 B.-2 C.±2 D.1或2
【答案】B
【详解】解:由抛物线y=m的开口向下,得:
,
m=-2,m=1(不符合题意要舍去),
故选:B.
典例精析
4.下列关于抛物线y=-(x+2)2-4的说法错误的是( )
A.有最大值-4
B.对称轴是直线x=-2
C.顶点坐标是(2,-3)
D.当x>0时,y随x的增大而减小
【答案】C
【详解】解:∵抛物线y=-(x+2)2-4,
∴函数开口向下,
∴当x=-2时,函数有最大值-4,
∴对称轴是直线x=-2,顶点坐标是(-2,-4),当x>-2时,y随x的增大而减小,
故A、B、D正确,不符合题意;C错误,符合题意;
故选:C.
典例精析
5.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=,由此可知铅球推出的距离是( )
A.10m B.3m C.4m D.2m或10m
【答案】A
【分析】当y=0时代入解析式y=,求出x的值就可以求出结论.
【详解】解:由题意,得
当y=0时,=0
解得:x1=10,x2=-2(舍去).
故选:A.
典例精析
6.已知,点A(x1,y1),B(x2,y2)在抛物线y=x2-4x+3上,若-1<x<1,存在一个正数m,当m-1<x2<m时,都有y1≠y2,则m的取值范围是( )
A.m≥2 B.2≤m≤3
C.2≤m≤3或m≥5 D.2≤m≤3或m≥6
【答案】D
【详解】解:∵抛物线解析式为y=x2-4x+3,
∴对称轴为x=2,由二次函数的对称性可知,
当x=-1和x=5时,函数值y相等,
当x=1和x=3时,函数值y相等,
即当满足-1<x<1和3<x<5的函数值相同,
当-1<x1<1,存在一个正数m,当m-1<x2<m时,都有y1≠y2,
∴或m-1≥5,解得2≤m≤3或m≥6;
故选:D.
典例精析
7.已知点A(0,m)、点B(3,n)为抛物线y=ax2-2ax+b上一点,且a>0,则m______n(填“>”或“<”).
【答案】<
【点睛】本题考查二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键.
典例精析
8.已知开口向上的抛物线y=x2-2x+3,在此抛物线上有A(,y1),B(2,y2)和C(3,y3)三点,则y1,y2和y3的大小关系为________.
【答案】y2<y1<y3
【点睛】本题考查了二次函数图像的性质;熟练运用二次函数图像的对称性和增减性是解题的关键.
典例精析
9.教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为y=,由此可知小明此次投掷的成绩是________m.
【答案】9
【点睛】本题是二次函数的实际应用题.理解当y=0时,x的正值代表的是铅球的落脚点离原点的距离是解题关键.
典例精析
10.在平面直角坐标系中,抛物线y=ax2-4ax+与y轴交于点A,过点A作x轴平行线交抛物线于点B,若点B关于(,0)的对称点C恰好落在抛物线上,则a值为_____.
【答案】
【分析】先根据二次函数的性质及题意求出点B的坐标,再根据对称的性质求出点C的坐标,最后将点C的坐标代入二次函数解析式求解即可.
典例精析
11.如图,已知抛物线y=ax2+c与直线y=kx+m交于A(-4,y1),B(1,y2)两点,则关于x的不等式ax2+c≥kx+m的解集是____.
【答案】-4≤x≤1
【点睛】本题考查了二次函数与不等式的关系,主要利用了数形结合的思想,解题关键在于对图像的理解,谁大谁的图象在上面.
典例精析
12.仙桃市大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全市学校的设施和设备进行全面改造,2020年市政府已投资7.5亿元人民币,若每年投资的增长率相同,预计2022年投资10.8亿元人民币,那么每年投资的增长率为_____.
【答案】20%
【详解】解:设每年投资的增长率为x,根据题意得,
7.5(1+x)2=10.8
解得:x1=0.2=20%,x2=-2.2(舍去)
故答案为:20%.
典例精析
13.已知抛物线y=-x2+4x+5.
(1)求抛物线与y轴交点的坐标;
(2)求抛物线的对称轴.
【详解】(1)解:令x=0,则y=-x2+4x+5=5,
抛物线与y轴交点的坐标为:(0,5);
(2)解:∵y=-x2+4x+5=-(x-2)2+9,
∴抛物线的对称轴为:x=2.
典例精析
14.如图,直线y1=x-1和抛物线y2=x2+bx+c都经过点A(1,0),B(3,2).
(1)求抛物线的解析式和顶点P的坐标;
(2)直接回答,当x为何值时,不等式x2+bc+c>x-1.
典例精析
【分析】(1)利用待定系数法求解析式并配方成顶点式即可.
(2)利用图像求二次函数图像高于一次函数图像的部分.
【答案】(1)抛物线的解析式为y2=x2-3x+2,抛物线的顶点P()
(2)当x<1或x>3时,x2+bx+c>x+1
典例精析
15.某课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)直接写出面积S与x的数量关系式并写出自变量的取值范围;
(2)若矩形生物苗圃园的面积为100平方米时,求垂直于墙的一边长为多少米?
(3)垂直于墙的一边长为多少米时,这个苗圃园的面积最大?
典例精析
【答案】(1)S=-2x2+30x,自变量取值范围为6≤x<15
(2)垂直于墙的一边长为10米
(3)垂直于墙的一边长为米时,这个苗圃园的面积最大
【分析】(1)根据题意可直接求解;
(2)由(1)可当S=100时代入求解即可;
(3)由(1)及结合二次函数的最值可进行求解.
典例精析
16.2022年2月4日,第24届冬季奥林匹克运动会在北京举行,吉祥物“冰墩墩”备受人民的喜爱.某商店经销一种吉祥物玩具,成本价为30元,经市场调查,每天销售量y(个)与销售单价x(元)之间的关系如图所示,规定该玩具的售价不能低于30元,且不高于80元.
(1)直接写出y与x之间的函数关系式;
(2)设每天的总利润为w元,当销售单价定为多少元时,该商店每天的利润最大?
(3)如果该商店销售这种玩具每天获得3600元的利润,那么该玩具的销售单价为多少元?
典例精析
【答案】(1)y=-x+180
(2)销售单价定为80元时,该超市每天的利润最大,最大利润5000元
(3)销售单价为60元
【分析】(1)根据函数图象将点(30,150)(80,100)代入一次函数表达式y=kx+b,即可求解.
(2)根据题意列出函数关系式,根据题意求得自变量的取值范围,根据二次函数的性质求得最值,
(3)根据题意列出一元二次方程,解方程,根据题意取舍结果,即可求解.
课堂小结
二次函数
图象画法
抛物线
开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
解析式
应用
第二章 二次函数
专题小结
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
知识归纳
知识点1 二次函数的定义
知识点2 二次函数的图象与性质
知识点3 二次函数y=ax2+bx+c的图象特征与系数a,b,c的关系
知识点4 二次函数图象的平移
知识点5 二次函数解析式的求解
知识点6 二次函数与一元二次方程的关系
知识点7 二次函数的应用
知识点总结
知识点一、二次函数的定义
1.一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.特别地,当a≠0,b=c=0时,y=ax2是二次函数的特殊形式.
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中x1,x2是图象与x轴交点的横坐标.
二次函数 y=a(x-h)2+k y=ax2+bx+c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 a>0 开口向上
a < 0 开口向下
x=h
(h , k)
y最小=k
y最大=k
在对称轴左边,x↗ y↘;在对称轴右边, x↗ y↗
在对称轴左边,x↗ y↗;在对称轴右边, x↗ y↘
y最小=
y最大=
知识点二、二次函数的图象和性质
知识点三、二次函数y=ax2+bx+c的图象特征与系数a,b,c的关系
项目字母 字母的符号 图像的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
知识点四、二次函数图象的平移
任意抛物线y=a(x-h)2+k可以由抛物线y=ax2经过平移得到,具体平移方法如下:
知识点五、二次函数表达式的求法
1.一般式:y=ax2+bx+c (a≠ 0)
若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
2.顶点式:y=a(x-h)2+k(a≠0)
若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将解析式化为一般式.
3.交点式:y=a(x-x1)(x-x2)(a≠0)
若已知二次函数图象与x轴的两个交点的坐标,则设交点式y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a的值,最后将解析式化为一般式.
知识点六、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
知识点七、二次函数的应用
2.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
典例精析
1.函数y=3x2-1的图象与y轴的交点坐标是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
【答案】C
【分析】根据y轴上点的坐标特征,令x=0即可求解.
【详解】解:令x=0,则y=-1,
∴函数y=3x2-1的图象与y轴的交点坐标是(0,-1),
故选:C
典例精析
2.二次函数y1=3x2+bx+c与一次函数y2=kx+m的图象交于点A(2,3)和点B(4,1),要使y1>y2,则x的取值范围是( )
A.x<2 B.x<4
C.2<x<4 D.x<2或x>4
【答案】D
【详解】解:∵二次函数y1=3x2+bx+c与一次函数y2=kx+m的图象交于点A(2,3)和点B(4,1),
又∵二次函数y1=3x2+bx+c的图像开口向上,
∴要使y1>y2,则x的取值范围是:x<2或x>4,
故选D.
典例精析
3.若抛物线y=m开口向下,则m的值为( )
A.2 B.-2 C.±2 D.1或2
【答案】B
【详解】解:由抛物线y=m的开口向下,得:
,
m=-2,m=1(不符合题意要舍去),
故选:B.
典例精析
4.下列关于抛物线y=-(x+2)2-4的说法错误的是( )
A.有最大值-4
B.对称轴是直线x=-2
C.顶点坐标是(2,-3)
D.当x>0时,y随x的增大而减小
【答案】C
【详解】解:∵抛物线y=-(x+2)2-4,
∴函数开口向下,
∴当x=-2时,函数有最大值-4,
∴对称轴是直线x=-2,顶点坐标是(-2,-4),当x>-2时,y随x的增大而减小,
故A、B、D正确,不符合题意;C错误,符合题意;
故选:C.
典例精析
5.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=,由此可知铅球推出的距离是( )
A.10m B.3m C.4m D.2m或10m
【答案】A
【分析】当y=0时代入解析式y=,求出x的值就可以求出结论.
【详解】解:由题意,得
当y=0时,=0
解得:x1=10,x2=-2(舍去).
故选:A.
典例精析
6.已知,点A(x1,y1),B(x2,y2)在抛物线y=x2-4x+3上,若-1<x<1,存在一个正数m,当m-1<x2<m时,都有y1≠y2,则m的取值范围是( )
A.m≥2 B.2≤m≤3
C.2≤m≤3或m≥5 D.2≤m≤3或m≥6
【答案】D
【详解】解:∵抛物线解析式为y=x2-4x+3,
∴对称轴为x=2,由二次函数的对称性可知,
当x=-1和x=5时,函数值y相等,
当x=1和x=3时,函数值y相等,
即当满足-1<x<1和3<x<5的函数值相同,
当-1<x1<1,存在一个正数m,当m-1<x2<m时,都有y1≠y2,
∴或m-1≥5,解得2≤m≤3或m≥6;
故选:D.
典例精析
7.已知点A(0,m)、点B(3,n)为抛物线y=ax2-2ax+b上一点,且a>0,则m______n(填“>”或“<”).
【答案】<
【点睛】本题考查二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键.
典例精析
8.已知开口向上的抛物线y=x2-2x+3,在此抛物线上有A(,y1),B(2,y2)和C(3,y3)三点,则y1,y2和y3的大小关系为________.
【答案】y2<y1<y3
【点睛】本题考查了二次函数图像的性质;熟练运用二次函数图像的对称性和增减性是解题的关键.
典例精析
9.教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为y=,由此可知小明此次投掷的成绩是________m.
【答案】9
【点睛】本题是二次函数的实际应用题.理解当y=0时,x的正值代表的是铅球的落脚点离原点的距离是解题关键.
典例精析
10.在平面直角坐标系中,抛物线y=ax2-4ax+与y轴交于点A,过点A作x轴平行线交抛物线于点B,若点B关于(,0)的对称点C恰好落在抛物线上,则a值为_____.
【答案】
【分析】先根据二次函数的性质及题意求出点B的坐标,再根据对称的性质求出点C的坐标,最后将点C的坐标代入二次函数解析式求解即可.
典例精析
11.如图,已知抛物线y=ax2+c与直线y=kx+m交于A(-4,y1),B(1,y2)两点,则关于x的不等式ax2+c≥kx+m的解集是____.
【答案】-4≤x≤1
【点睛】本题考查了二次函数与不等式的关系,主要利用了数形结合的思想,解题关键在于对图像的理解,谁大谁的图象在上面.
典例精析
12.仙桃市大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全市学校的设施和设备进行全面改造,2020年市政府已投资7.5亿元人民币,若每年投资的增长率相同,预计2022年投资10.8亿元人民币,那么每年投资的增长率为_____.
【答案】20%
【详解】解:设每年投资的增长率为x,根据题意得,
7.5(1+x)2=10.8
解得:x1=0.2=20%,x2=-2.2(舍去)
故答案为:20%.
典例精析
13.已知抛物线y=-x2+4x+5.
(1)求抛物线与y轴交点的坐标;
(2)求抛物线的对称轴.
【详解】(1)解:令x=0,则y=-x2+4x+5=5,
抛物线与y轴交点的坐标为:(0,5);
(2)解:∵y=-x2+4x+5=-(x-2)2+9,
∴抛物线的对称轴为:x=2.
典例精析
14.如图,直线y1=x-1和抛物线y2=x2+bx+c都经过点A(1,0),B(3,2).
(1)求抛物线的解析式和顶点P的坐标;
(2)直接回答,当x为何值时,不等式x2+bc+c>x-1.
典例精析
【分析】(1)利用待定系数法求解析式并配方成顶点式即可.
(2)利用图像求二次函数图像高于一次函数图像的部分.
【答案】(1)抛物线的解析式为y2=x2-3x+2,抛物线的顶点P()
(2)当x<1或x>3时,x2+bx+c>x+1
典例精析
15.某课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)直接写出面积S与x的数量关系式并写出自变量的取值范围;
(2)若矩形生物苗圃园的面积为100平方米时,求垂直于墙的一边长为多少米?
(3)垂直于墙的一边长为多少米时,这个苗圃园的面积最大?
典例精析
【答案】(1)S=-2x2+30x,自变量取值范围为6≤x<15
(2)垂直于墙的一边长为10米
(3)垂直于墙的一边长为米时,这个苗圃园的面积最大
【分析】(1)根据题意可直接求解;
(2)由(1)可当S=100时代入求解即可;
(3)由(1)及结合二次函数的最值可进行求解.
典例精析
16.2022年2月4日,第24届冬季奥林匹克运动会在北京举行,吉祥物“冰墩墩”备受人民的喜爱.某商店经销一种吉祥物玩具,成本价为30元,经市场调查,每天销售量y(个)与销售单价x(元)之间的关系如图所示,规定该玩具的售价不能低于30元,且不高于80元.
(1)直接写出y与x之间的函数关系式;
(2)设每天的总利润为w元,当销售单价定为多少元时,该商店每天的利润最大?
(3)如果该商店销售这种玩具每天获得3600元的利润,那么该玩具的销售单价为多少元?
典例精析
【答案】(1)y=-x+180
(2)销售单价定为80元时,该超市每天的利润最大,最大利润5000元
(3)销售单价为60元
【分析】(1)根据函数图象将点(30,150)(80,100)代入一次函数表达式y=kx+b,即可求解.
(2)根据题意列出函数关系式,根据题意求得自变量的取值范围,根据二次函数的性质求得最值,
(3)根据题意列出一元二次方程,解方程,根据题意取舍结果,即可求解.
课堂小结
二次函数
图象画法
抛物线
开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
解析式
应用
