19.6 轨迹(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 19.6 轨迹(第1课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
19.6轨迹(第1课时)
第 19 章 几何证明
八年级上册数学沪教版
●
●
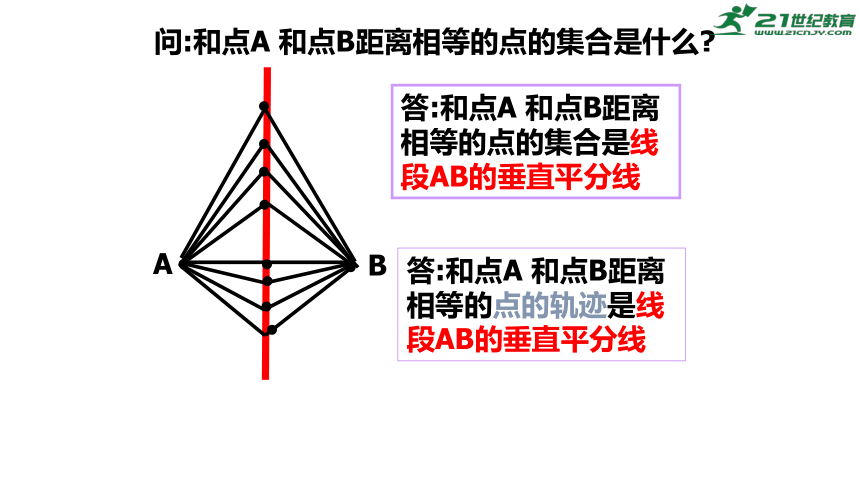
A
B
问:和点A 和点B距离相等的点的集合是什么
●
●
●
●
●
●
●
●
答:和点A 和点B距离相等的点的集合是线段AB的垂直平分线
答:和点A 和点B距离相等的点的轨迹是线段AB的垂直平分线
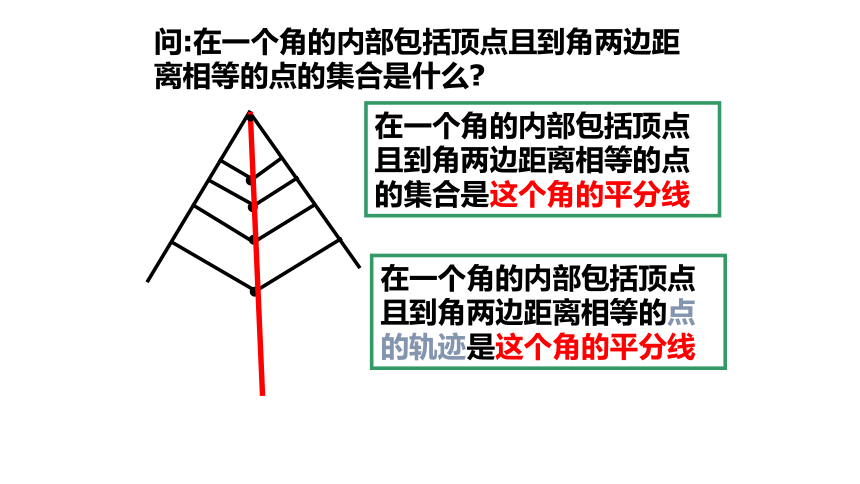
问:在一个角的内部包括顶点且到角两边距离相等的点的集合是什么
●
●
●
●
●
在一个角的内部包括顶点且到角两边距离相等的点的集合是这个角的平分线
在一个角的内部包括顶点且到角两边距离相等的点的轨迹是这个角的平分线
轨迹的定义
点的轨迹:符合某些条件的
所有的 点的集合.
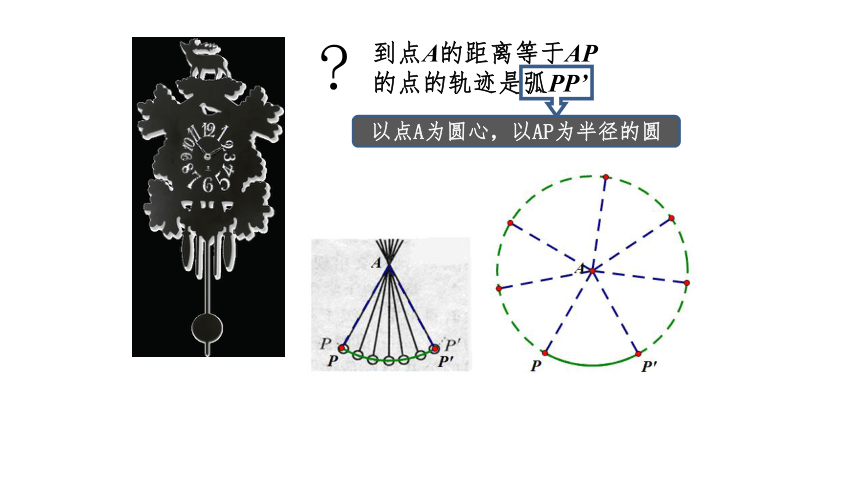
到点A的距离等于AP
的点的轨迹是弧PP’
以点A为圆心,以AP为半径的圆
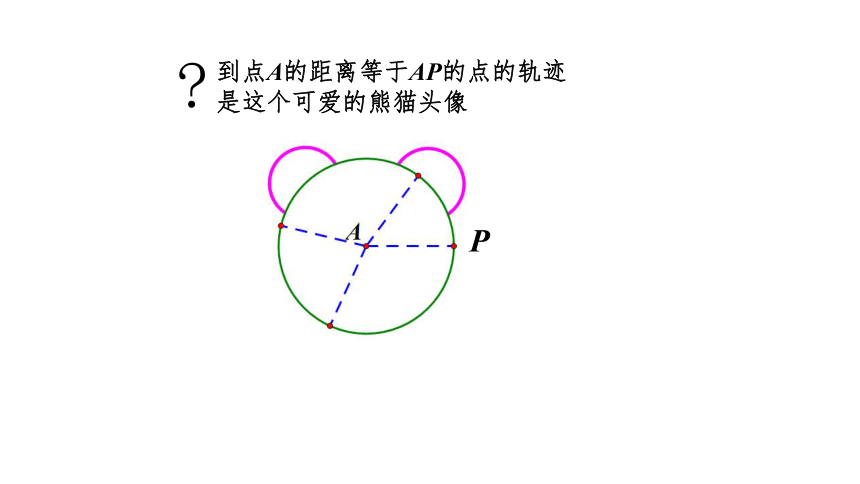
到点A的距离等于AP的点的轨迹是这个可爱的熊猫头像
P
基本轨迹
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
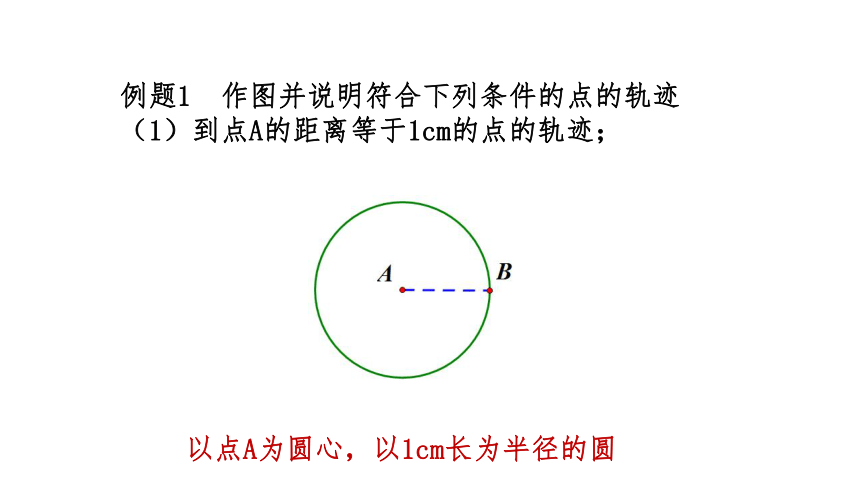
例题1 作图并说明符合下列条件的点的轨迹
(1)到点A的距离等于1cm的点的轨迹;
以点A为圆心,以1cm长为半径的圆
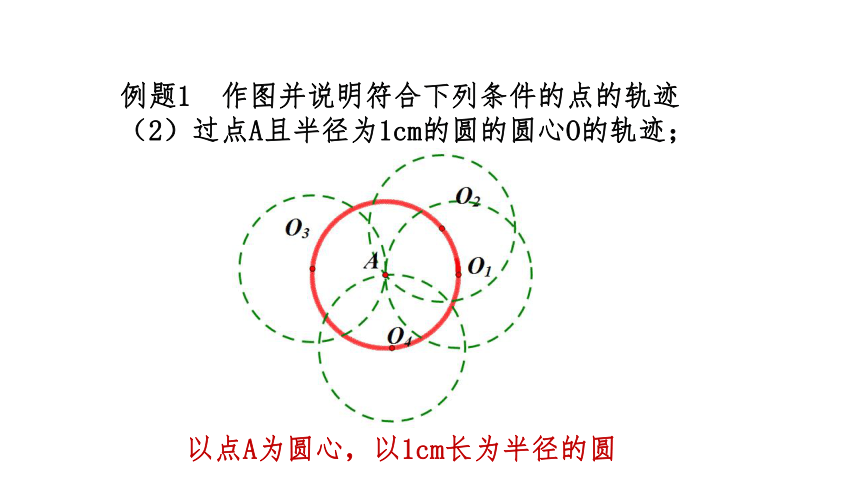
例题1 作图并说明符合下列条件的点的轨迹
(2)过点A且半径为1cm的圆的圆心O的轨迹;
以点A为圆心,以1cm长为半径的圆
求作点的轨迹的步骤:
找(找出几个符合条件的图形,确定点的位置);
连(通过已有点猜测出点的轨迹,并连线);
查(通过两方面来验证轨迹,确保不多不漏);
说(描述轨迹,去掉不符合条件的点);
F2:化归为基本轨迹
F1:描点法
线段AB的垂直平分线
例题2 作图并说明符合下列条件的点的轨迹
(1)和定点A、B距离相等的点C的轨迹;
基本轨迹
线段的垂直平分线
________________________点的集合是线段的垂直平分线
和线段两个端点距离相等的点的轨迹是线段的垂直平分线
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
例题2 作图并说明符合下列条件的点的轨迹
(2)经过定点A、B的圆的圆心O的轨迹;
线段AB的垂直平分线
线段AB的垂直平分线(除线段AB的中点外)
例题2 作图并说明符合下列条件的点的轨迹
(3)以线段AB为底边的等腰三角形的顶点C的轨迹;
平行于AB且与AB距离为1cm的两条平行线.
例题3 作图并说明符合下列条件的点的轨迹
(1)与直线AB的距离为1cm的点的轨迹;
平行于AB、CD且与AB、CD距离相等的平行线.
例题3 作图并说明符合下列条件的点的轨迹
(2)与平行直线AB、CD的距离相等的点的轨迹;
∠AOB的角平分线
例题3 作图并说明符合下列条件的点的轨迹
(3)在∠AOB内部,到角两边距离相等的点的轨迹;
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
基本轨迹
线段的垂直平分线
角的平分线
________________________点的集合是线段的垂直平分线
和线段两个端点距离相等的点的轨迹是线段的垂直平分线
______________________________________________点的集合是这个角的平分线
在一个角的内部(包括顶点)且到角两边距离相等的点的轨迹是这个角的平分线
例题3 作图并说明符合下列条件的点的轨迹.
(4)与相交直线AB、CD的距离相等的点的轨迹.
平分直线AB、CD所成角的两条互相垂直的直线.
例题4 作图并说明符合下列条件的点的轨迹.
(1)已知两个定点A、B,这两点的距离为3cm,说出到点A、B的距离之和为3cm的点的轨迹。
线段AB.
例题4 作图并说明符合下列条件的点的轨迹.
(2)已知两个定点A、B,这两点的距离为3cm,说出到点A、B的距离之和为3cm的点的轨迹。
差
线段AB的延长线与反向延长线.
课本练习
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
A
B
P
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
O
A
B
P
E
D
课堂小结
3.到定点的距离等于定长的点的轨迹是
____________________________________________________________
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
以这个定点为圆心、定长为半径的圆
课堂小结
THANKS
“
”
19.6轨迹(第1课时)
第 19 章 几何证明
八年级上册数学沪教版
●
●
A
B
问:和点A 和点B距离相等的点的集合是什么
●
●
●
●
●
●
●
●
答:和点A 和点B距离相等的点的集合是线段AB的垂直平分线
答:和点A 和点B距离相等的点的轨迹是线段AB的垂直平分线
问:在一个角的内部包括顶点且到角两边距离相等的点的集合是什么
●
●
●
●
●
在一个角的内部包括顶点且到角两边距离相等的点的集合是这个角的平分线
在一个角的内部包括顶点且到角两边距离相等的点的轨迹是这个角的平分线
轨迹的定义
点的轨迹:符合某些条件的
所有的 点的集合.
到点A的距离等于AP
的点的轨迹是弧PP’
以点A为圆心,以AP为半径的圆
到点A的距离等于AP的点的轨迹是这个可爱的熊猫头像
P
基本轨迹
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
例题1 作图并说明符合下列条件的点的轨迹
(1)到点A的距离等于1cm的点的轨迹;
以点A为圆心,以1cm长为半径的圆
例题1 作图并说明符合下列条件的点的轨迹
(2)过点A且半径为1cm的圆的圆心O的轨迹;
以点A为圆心,以1cm长为半径的圆
求作点的轨迹的步骤:
找(找出几个符合条件的图形,确定点的位置);
连(通过已有点猜测出点的轨迹,并连线);
查(通过两方面来验证轨迹,确保不多不漏);
说(描述轨迹,去掉不符合条件的点);
F2:化归为基本轨迹
F1:描点法
线段AB的垂直平分线
例题2 作图并说明符合下列条件的点的轨迹
(1)和定点A、B距离相等的点C的轨迹;
基本轨迹
线段的垂直平分线
________________________点的集合是线段的垂直平分线
和线段两个端点距离相等的点的轨迹是线段的垂直平分线
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
例题2 作图并说明符合下列条件的点的轨迹
(2)经过定点A、B的圆的圆心O的轨迹;
线段AB的垂直平分线
线段AB的垂直平分线(除线段AB的中点外)
例题2 作图并说明符合下列条件的点的轨迹
(3)以线段AB为底边的等腰三角形的顶点C的轨迹;
平行于AB且与AB距离为1cm的两条平行线.
例题3 作图并说明符合下列条件的点的轨迹
(1)与直线AB的距离为1cm的点的轨迹;
平行于AB、CD且与AB、CD距离相等的平行线.
例题3 作图并说明符合下列条件的点的轨迹
(2)与平行直线AB、CD的距离相等的点的轨迹;
∠AOB的角平分线
例题3 作图并说明符合下列条件的点的轨迹
(3)在∠AOB内部,到角两边距离相等的点的轨迹;
到定点的距离等于定长的点的轨迹是以定点为圆心定长为半径的圆.
基本轨迹
线段的垂直平分线
角的平分线
________________________点的集合是线段的垂直平分线
和线段两个端点距离相等的点的轨迹是线段的垂直平分线
______________________________________________点的集合是这个角的平分线
在一个角的内部(包括顶点)且到角两边距离相等的点的轨迹是这个角的平分线
例题3 作图并说明符合下列条件的点的轨迹.
(4)与相交直线AB、CD的距离相等的点的轨迹.
平分直线AB、CD所成角的两条互相垂直的直线.
例题4 作图并说明符合下列条件的点的轨迹.
(1)已知两个定点A、B,这两点的距离为3cm,说出到点A、B的距离之和为3cm的点的轨迹。
线段AB.
例题4 作图并说明符合下列条件的点的轨迹.
(2)已知两个定点A、B,这两点的距离为3cm,说出到点A、B的距离之和为3cm的点的轨迹。
差
线段AB的延长线与反向延长线.
课本练习
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
A
B
P
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
O
A
B
P
E
D
课堂小结
3.到定点的距离等于定长的点的轨迹是
____________________________________________________________
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
以这个定点为圆心、定长为半径的圆
课堂小结
THANKS
“
”
