19.5 角的平分线(第1课时) 课件 (共16张PPT)
文档属性
| 名称 | 19.5 角的平分线(第1课时) 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:30:22 | ||
图片预览




文档简介
(共16张PPT)
19.5角的平分线(第1课时)
第 19 章 几何证明
八年级上册数学沪教版
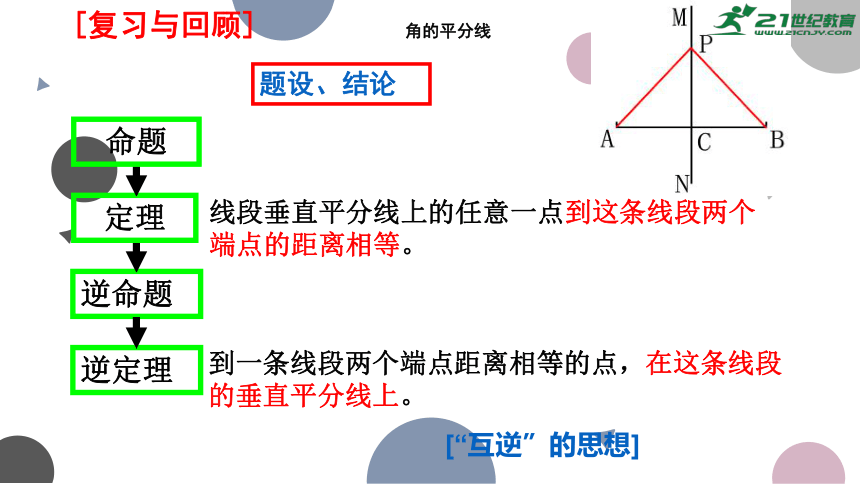
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
[复习与回顾]
线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
题设、结论
[“互逆”的思想]
逆命题
逆定理
定理
命题
角的平分线
“角”是轴对称图形,它的对称轴是什么?
A
B
O
1
2
“角的平分线”除了平分这个角以外,还有其他的性质吗?
角平分线所在直线
C
∵OC平分∠AOB,
∴∠1=∠2
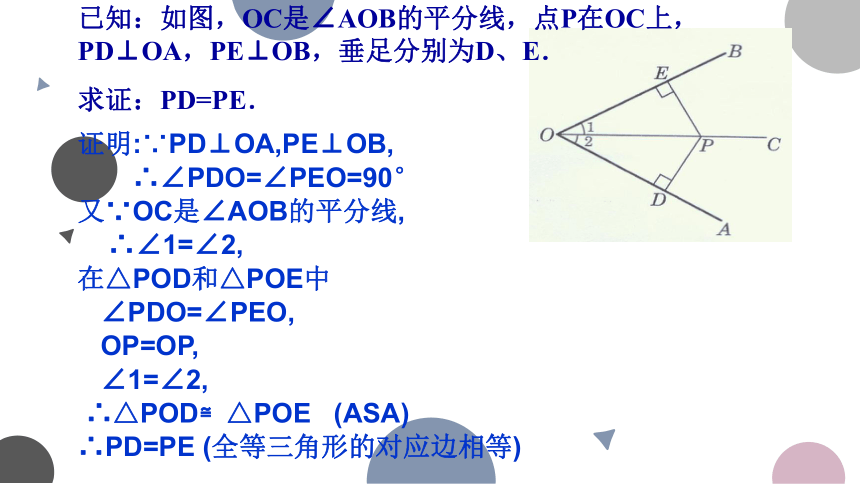
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°
又∵OC是∠AOB的平分线,
∴∠1=∠2,
在△POD和△POE中
∠PDO=∠PEO,
OP=OP,
∠1=∠2,
∴△POD≌△POE (ASA)
∴PD=PE (全等三角形的对应边相等)
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
探寻逆定理
在角的平分线上的点到这个角两边的距离相等。
逆命题:
到这个角两边距离相等的点,在这个角的平分线上。
在一个角的内部(包括顶点)且
证明逆命题
已知:如图,PD⊥OA,PE⊥OB,垂足分别为D、E,且PD=PE
求证:P在∠AOB角平分线上
∠1=∠2
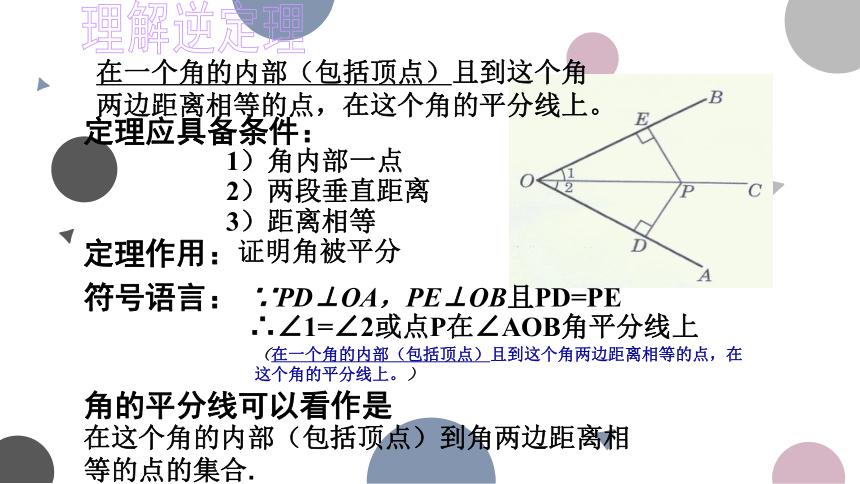
在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上。
角的平分线可以看作是
在这个角的内部(包括顶点)到角两边距离相等的点的集合.
符号语言:
∵PD⊥OA,PE⊥OB且PD=PE
定理应具备条件:
1)角内部一点
2)两段垂直距离
3)距离相等
定理作用:
证明角被平分
理解逆定理
∴∠1=∠2或点P在∠AOB角平分线上
(在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上。)
用集合的思想理解角平分线:
A
B
O
C
角的平分线可以看作是在这个角的内部(包括顶点)到角两边距离相等的点的集合.
类比探究
求证:点O在∠C的平分线上.
[例1]如图,AO、BO分别是∠A、∠B的平分线, OD⊥BC,OE⊥AB,垂足分别为D、E.
F
∵AO平分∠BAC,OE⊥AB(已知)
证明:过点O作OF⊥AC,垂足是F。
∴OE=OF(在角的平分线上的点到这个角的两边的距离相等)
∴OF=OD(等量代换)
∴点O在∠C的平分线上(在一个角的内部且到角的两边距离相等的点,在这个角的平分线上)
OF⊥AC(作图)
本例结论可引申为——
这个点叫做“三角形的内心”。
三角形三个内角的平分线交于一点,
同理,OE=OD
课本练习
2. 已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB,PN⊥AC,点M、N分别为垂足.
求证(1)PM=PN
(2)AP平分∠MAN.
H
PM=PH
PN=PH
PM=PN
证明:
过点P作PH⊥BC,垂足为点H.
∵BP是∠MBC的平分线
(已知),
PM⊥AB,PH⊥BC
∴PM=PH
(在角的平分线上的点到这个角两边的距离相等),
同理:PN=PH.
∴PM=PN(等量代换).
∴点P在∠MAN的平分线上,即AP平分∠MAN.
(在一个角的内部(包括顶点)且到角两边距离相等的点,在这个角的平分线上).
通过这节课的学习,你有什么收获和体会?
1.角的平分线的性质定理:
在角的平分线上的点到这个角两边的距离相等.
符号语言:
∵OP平分∠AOB
PD⊥OA,PE⊥OB,
∴PD=PE
(在角的平分线上的点到这个角两边的距离相等).
课堂小结
2.角平分线性质定理的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.
符号语言:
∴OP平分∠AOB
∵PD⊥OA,PE⊥OB,
PD=PE.
(在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上).
3. 三角形的三条角平分线交于一点,且这点到三边的距离相等.
D
E
F
G
H
S
∵∠1=∠2,∠3 =∠4,∠5=∠6
1
2
3
4
5
6
∴ AG、BH、 CS交于点O.
又 OD⊥BC, OE⊥AB, OF⊥AC,垂足分别为D、E、F,
∴ OD=OE=OF.
THANKS
“
”
19.5角的平分线(第1课时)
第 19 章 几何证明
八年级上册数学沪教版
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
[复习与回顾]
线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
题设、结论
[“互逆”的思想]
逆命题
逆定理
定理
命题
角的平分线
“角”是轴对称图形,它的对称轴是什么?
A
B
O
1
2
“角的平分线”除了平分这个角以外,还有其他的性质吗?
角平分线所在直线
C
∵OC平分∠AOB,
∴∠1=∠2
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°
又∵OC是∠AOB的平分线,
∴∠1=∠2,
在△POD和△POE中
∠PDO=∠PEO,
OP=OP,
∠1=∠2,
∴△POD≌△POE (ASA)
∴PD=PE (全等三角形的对应边相等)
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
探寻逆定理
在角的平分线上的点到这个角两边的距离相等。
逆命题:
到这个角两边距离相等的点,在这个角的平分线上。
在一个角的内部(包括顶点)且
证明逆命题
已知:如图,PD⊥OA,PE⊥OB,垂足分别为D、E,且PD=PE
求证:P在∠AOB角平分线上
∠1=∠2
在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上。
角的平分线可以看作是
在这个角的内部(包括顶点)到角两边距离相等的点的集合.
符号语言:
∵PD⊥OA,PE⊥OB且PD=PE
定理应具备条件:
1)角内部一点
2)两段垂直距离
3)距离相等
定理作用:
证明角被平分
理解逆定理
∴∠1=∠2或点P在∠AOB角平分线上
(在一个角的内部(包括顶点)且到这个角两边距离相等的点,在这个角的平分线上。)
用集合的思想理解角平分线:
A
B
O
C
角的平分线可以看作是在这个角的内部(包括顶点)到角两边距离相等的点的集合.
类比探究
求证:点O在∠C的平分线上.
[例1]如图,AO、BO分别是∠A、∠B的平分线, OD⊥BC,OE⊥AB,垂足分别为D、E.
F
∵AO平分∠BAC,OE⊥AB(已知)
证明:过点O作OF⊥AC,垂足是F。
∴OE=OF(在角的平分线上的点到这个角的两边的距离相等)
∴OF=OD(等量代换)
∴点O在∠C的平分线上(在一个角的内部且到角的两边距离相等的点,在这个角的平分线上)
OF⊥AC(作图)
本例结论可引申为——
这个点叫做“三角形的内心”。
三角形三个内角的平分线交于一点,
同理,OE=OD
课本练习
2. 已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB,PN⊥AC,点M、N分别为垂足.
求证(1)PM=PN
(2)AP平分∠MAN.
H
PM=PH
PN=PH
PM=PN
证明:
过点P作PH⊥BC,垂足为点H.
∵BP是∠MBC的平分线
(已知),
PM⊥AB,PH⊥BC
∴PM=PH
(在角的平分线上的点到这个角两边的距离相等),
同理:PN=PH.
∴PM=PN(等量代换).
∴点P在∠MAN的平分线上,即AP平分∠MAN.
(在一个角的内部(包括顶点)且到角两边距离相等的点,在这个角的平分线上).
通过这节课的学习,你有什么收获和体会?
1.角的平分线的性质定理:
在角的平分线上的点到这个角两边的距离相等.
符号语言:
∵OP平分∠AOB
PD⊥OA,PE⊥OB,
∴PD=PE
(在角的平分线上的点到这个角两边的距离相等).
课堂小结
2.角平分线性质定理的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.
符号语言:
∴OP平分∠AOB
∵PD⊥OA,PE⊥OB,
PD=PE.
(在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上).
3. 三角形的三条角平分线交于一点,且这点到三边的距离相等.
D
E
F
G
H
S
∵∠1=∠2,∠3 =∠4,∠5=∠6
1
2
3
4
5
6
∴ AG、BH、 CS交于点O.
又 OD⊥BC, OE⊥AB, OF⊥AC,垂足分别为D、E、F,
∴ OD=OE=OF.
THANKS
“
”
