15.3.3 分式方程的应用 课件 (共28张PPT)
文档属性
| 名称 | 15.3.3 分式方程的应用 课件 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:26:07 | ||
图片预览








文档简介
(共28张PPT)
分式方程的实际应用
1.理解数量关系正确列出分式方程.(难点)
2.在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.
(重点)
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
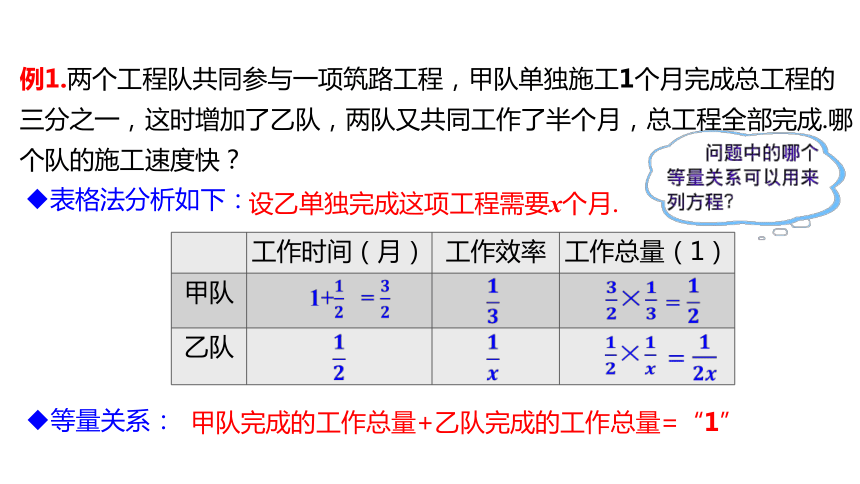
例1.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
1+
=
×
×
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
设乙单独完成这项工程需要x个月.则乙队的工作效率是( )甲队的工作效率是( ),合作的工作效率是( ).
此时方程是:
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如××单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2指该类问题中的“两个主人公”如甲队和乙队,或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
列分式方程解决工程问题的解题策略:
甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求甲、乙每小时各做零件多少个.
解:设乙每小时做零件 x 个,则甲每小时做零件(x +6)个,根据题意,得
方程两边同乘x(x+6),得 90x=60(x+6)
解得 x=12
检验:x=12时x(x+6)≠0,
所以,原分式方程的解为x=12.
答:甲、乙每小时分别做零件18个、12个.
例2.某次列车平均提速vkm/h. 用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
分析:这里的字母v,s表示已知数据,设提速前列车的平均速度为xkm/h,那么提速前列车行驶skm所用时间为_____h,提速后列车的平均速度为_____ km/h,提速后列车运行(s+50)km所用时间为________h.
(x+v)
根据行驶时间的等量关系可以列出方程.
例2.某次列车平均提速vkm/h. 用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
解:设提速前列车的平均速度为xkm/h,根据行驶时间的等量关系,得
方程两边乘x(x+v),得 s(x+v)=x(s+50)
解得
检验:由于v,s都是正数,得 时x(x+v)≠0.
所以,原分式方程的解为 .
答:提速前列车的平均速度为 km/h.
1.注意关键词“提速”与“提速到”的区别;
2.明确两个“主人公”的行程问题中三个量用代数式表示出来;
3.行程问题中的等量关系通常抓住“时间线”来建立方程.
列分式方程解决行程问题的解题策略:
八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.
解:设骑车学生的速度为xkm/h,则汽车的速度为2xkm/h,根据题意,得
方程两边同乘6x,得 60-30=2x
解得 x=15
检验:x=15时6x≠0,所以,原分式方程的解为x=15.
答:骑车学生的速度为15km/h.
例3.某经销商销售的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份每台冰箱的售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(),请问有几种进货方案?
(1)解:设二月份冰箱每台售价为x元,则一月份每台售价元,
依题意得
解得
经检验可知是原方程的根.
∴二月份冰箱每台售价为4000元.
例3.某经销商销售的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份每台冰箱的售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(),请问有几种进货方案?
(2)依题意得:
解得,
∵,且是正整数,
∴,9,10,11,12
∴共有五种购物方案.
2022年第二十四届冬奥会在我国成功举办,吉祥物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(1)求第一次购进的“冰墩墩”玩具每件的进价;
(1)解:设第一次购进的“冰墩墩”玩具每件的进价为x元,则第二次每件的进价为元,
依题意得:,
解得:,
经检验:是方程的解,且符合题意,
答:第一次购进的“冰墩墩”玩具每件的进价为50元.
2022年第二十四届冬奥会在我国成功举办,吉祥物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(2)若两次购进的“冰墩墩”玩具每件售价均为75元,且全部售完,求两次的利润总和.
(2)解:由题意可得(元),
答:两次的总利润为2250元.
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根;(2)是否符合题意);
6.写:答案.
1.福建三明市套宁县发生山体滑坡后,周边市县为了应对,决定对4800米长的河提进行加固,在加固工程中,该地驻军出色地完成了任务,它们在加固600米后,采用了新的加固模式,每天加固的长度是原来的2倍,结果只用9天就完成了加固任务.求该地驻军原来每天加固大坝的米数?设原来每天加固x米,则下列所列方程正确的是( )
A. B.
C. D.
B
2.武汉新冠肺炎疫情爆发后,某省紧急组织调运一批医疗物资,由车队送往距离出发地900千米的武汉,出发第一小时内按原计划速度匀速行驶,一小时后以原来速度的1.2倍匀速行驶,因此比原计划提前2小时到达目的地.设原计划速度为x千米/时,则根据题意可列方程为( )
A. B.
C. D.
A
3.在创建文明县城的进程中,我县为美化县城环境,计划植树20万棵,由于志愿者的加入,实际每天植树比原计划多,结果提前3天完成任务,设原计划每天植树x万棵,由题意得到的方程是( )
A. B.
C. D.
A
4.某工程队在中山路改造一条长3000米的人行道,为尽量减少施工对交通造成的影响,施工时“×××”,设实际每天改造人行道米,则可得方程,根据已有信息,题中用“×××”表示的缺失的条件应补充为( )
A.每天比原计划少铺设20米,结果延迟10天完成
B.每天比原计划多铺设20米,结果延迟10天完成
C.每天比原计划多铺设20米,结果提前10天完成
D.每天比原计划少铺设20米,结果提前10天完成
C
5.在防疫新型冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用元购进医用口罩若干个,第二次又用元购进该款口罩,但第二次每个口罩的进价是第一次进价的倍,购进的数量比第一次少个.则第一次和第二次共购进的医用口罩数量______个.
1800
6.受疫情的影响,“84”消毒液需求量猛增,某商场用4000元购进一批“84”消毒液后,供不应求,商场又用6750元购进第二批这种消毒液,所购的瓶数是第一批瓶数的1.5倍,但每瓶单价贵了1元,则该商场第一批购进“84”清毒液每瓶的单价为______元.
8
7.在实施“中小学生蛋奶工程”中,某配送公司按上级要求,每周向学校配送鸡蛋10000个,鸡蛋用甲、乙两种不同规格的包装箱进行包装,若单独使用甲型包装箱比单独使用乙型包装箱可少用10个,每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋,设每个甲型包装箱可装个鸡蛋,根据题意可列方程为__________________.
8.科技创新加速中国高铁技术发展,某建筑集团承担一座高架桥的铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:
记者:你们是用10天完成4500米长的高架桥铺设任务的?
工程师:是的,我们铺设500米后,采用新的铺设技术,这样每天铺设长度是原来的2倍.
(1)通过这段对话,请你求出该建筑集团原来每天铺设高架桥的长度.
(2)请求出该建筑集团是提前多少天完成铺设任务的?
(1)解:设该建筑集团原来每天铺设高架桥x米,则采用新的铺设技术后每天铺设高架桥2x米,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
答:该建筑集团原来每天铺设高架桥300米;
(2)解:,
答:该建筑集团提前8天完成铺设任务.
9.在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知这项改造工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)若两队合做这项工程,求完成工程所需的天数.
(3)若甲队的费用每天1200元,乙队每天850元,可以有哪些施工方案?怎样施工费用最低?
(1)设乙单独完成该工程需要x天,
依题意得:,
解得:x=60,
经检验得,x=60是原方程的解,
答:乙单独完成该工程需要60天;
(2)两队合作需要时间:,
即两队合作需要24天;
(3)共有三种施工方案:①由甲单独完成,需40天,
施工费用:40×1200=48000元;
②由乙单独完成,需60天,
施工费用:60×850=51000元;
③由甲乙合作完成,需24天,
施工费用:24×(1200+850)=49200元;
∴由甲单独完成施工费用最低.
分式方程的实际应用
1.理解数量关系正确列出分式方程.(难点)
2.在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.
(重点)
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
例1.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
1+
=
×
×
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
设乙单独完成这项工程需要x个月.则乙队的工作效率是( )甲队的工作效率是( ),合作的工作效率是( ).
此时方程是:
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如××单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2指该类问题中的“两个主人公”如甲队和乙队,或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
列分式方程解决工程问题的解题策略:
甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求甲、乙每小时各做零件多少个.
解:设乙每小时做零件 x 个,则甲每小时做零件(x +6)个,根据题意,得
方程两边同乘x(x+6),得 90x=60(x+6)
解得 x=12
检验:x=12时x(x+6)≠0,
所以,原分式方程的解为x=12.
答:甲、乙每小时分别做零件18个、12个.
例2.某次列车平均提速vkm/h. 用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
分析:这里的字母v,s表示已知数据,设提速前列车的平均速度为xkm/h,那么提速前列车行驶skm所用时间为_____h,提速后列车的平均速度为_____ km/h,提速后列车运行(s+50)km所用时间为________h.
(x+v)
根据行驶时间的等量关系可以列出方程.
例2.某次列车平均提速vkm/h. 用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
解:设提速前列车的平均速度为xkm/h,根据行驶时间的等量关系,得
方程两边乘x(x+v),得 s(x+v)=x(s+50)
解得
检验:由于v,s都是正数,得 时x(x+v)≠0.
所以,原分式方程的解为 .
答:提速前列车的平均速度为 km/h.
1.注意关键词“提速”与“提速到”的区别;
2.明确两个“主人公”的行程问题中三个量用代数式表示出来;
3.行程问题中的等量关系通常抓住“时间线”来建立方程.
列分式方程解决行程问题的解题策略:
八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.
解:设骑车学生的速度为xkm/h,则汽车的速度为2xkm/h,根据题意,得
方程两边同乘6x,得 60-30=2x
解得 x=15
检验:x=15时6x≠0,所以,原分式方程的解为x=15.
答:骑车学生的速度为15km/h.
例3.某经销商销售的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份每台冰箱的售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(),请问有几种进货方案?
(1)解:设二月份冰箱每台售价为x元,则一月份每台售价元,
依题意得
解得
经检验可知是原方程的根.
∴二月份冰箱每台售价为4000元.
例3.某经销商销售的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份每台冰箱的售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(),请问有几种进货方案?
(2)依题意得:
解得,
∵,且是正整数,
∴,9,10,11,12
∴共有五种购物方案.
2022年第二十四届冬奥会在我国成功举办,吉祥物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(1)求第一次购进的“冰墩墩”玩具每件的进价;
(1)解:设第一次购进的“冰墩墩”玩具每件的进价为x元,则第二次每件的进价为元,
依题意得:,
解得:,
经检验:是方程的解,且符合题意,
答:第一次购进的“冰墩墩”玩具每件的进价为50元.
2022年第二十四届冬奥会在我国成功举办,吉祥物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(2)若两次购进的“冰墩墩”玩具每件售价均为75元,且全部售完,求两次的利润总和.
(2)解:由题意可得(元),
答:两次的总利润为2250元.
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根;(2)是否符合题意);
6.写:答案.
1.福建三明市套宁县发生山体滑坡后,周边市县为了应对,决定对4800米长的河提进行加固,在加固工程中,该地驻军出色地完成了任务,它们在加固600米后,采用了新的加固模式,每天加固的长度是原来的2倍,结果只用9天就完成了加固任务.求该地驻军原来每天加固大坝的米数?设原来每天加固x米,则下列所列方程正确的是( )
A. B.
C. D.
B
2.武汉新冠肺炎疫情爆发后,某省紧急组织调运一批医疗物资,由车队送往距离出发地900千米的武汉,出发第一小时内按原计划速度匀速行驶,一小时后以原来速度的1.2倍匀速行驶,因此比原计划提前2小时到达目的地.设原计划速度为x千米/时,则根据题意可列方程为( )
A. B.
C. D.
A
3.在创建文明县城的进程中,我县为美化县城环境,计划植树20万棵,由于志愿者的加入,实际每天植树比原计划多,结果提前3天完成任务,设原计划每天植树x万棵,由题意得到的方程是( )
A. B.
C. D.
A
4.某工程队在中山路改造一条长3000米的人行道,为尽量减少施工对交通造成的影响,施工时“×××”,设实际每天改造人行道米,则可得方程,根据已有信息,题中用“×××”表示的缺失的条件应补充为( )
A.每天比原计划少铺设20米,结果延迟10天完成
B.每天比原计划多铺设20米,结果延迟10天完成
C.每天比原计划多铺设20米,结果提前10天完成
D.每天比原计划少铺设20米,结果提前10天完成
C
5.在防疫新型冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用元购进医用口罩若干个,第二次又用元购进该款口罩,但第二次每个口罩的进价是第一次进价的倍,购进的数量比第一次少个.则第一次和第二次共购进的医用口罩数量______个.
1800
6.受疫情的影响,“84”消毒液需求量猛增,某商场用4000元购进一批“84”消毒液后,供不应求,商场又用6750元购进第二批这种消毒液,所购的瓶数是第一批瓶数的1.5倍,但每瓶单价贵了1元,则该商场第一批购进“84”清毒液每瓶的单价为______元.
8
7.在实施“中小学生蛋奶工程”中,某配送公司按上级要求,每周向学校配送鸡蛋10000个,鸡蛋用甲、乙两种不同规格的包装箱进行包装,若单独使用甲型包装箱比单独使用乙型包装箱可少用10个,每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋,设每个甲型包装箱可装个鸡蛋,根据题意可列方程为__________________.
8.科技创新加速中国高铁技术发展,某建筑集团承担一座高架桥的铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:
记者:你们是用10天完成4500米长的高架桥铺设任务的?
工程师:是的,我们铺设500米后,采用新的铺设技术,这样每天铺设长度是原来的2倍.
(1)通过这段对话,请你求出该建筑集团原来每天铺设高架桥的长度.
(2)请求出该建筑集团是提前多少天完成铺设任务的?
(1)解:设该建筑集团原来每天铺设高架桥x米,则采用新的铺设技术后每天铺设高架桥2x米,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
答:该建筑集团原来每天铺设高架桥300米;
(2)解:,
答:该建筑集团提前8天完成铺设任务.
9.在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知这项改造工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)若两队合做这项工程,求完成工程所需的天数.
(3)若甲队的费用每天1200元,乙队每天850元,可以有哪些施工方案?怎样施工费用最低?
(1)设乙单独完成该工程需要x天,
依题意得:,
解得:x=60,
经检验得,x=60是原方程的解,
答:乙单独完成该工程需要60天;
(2)两队合作需要时间:,
即两队合作需要24天;
(3)共有三种施工方案:①由甲单独完成,需40天,
施工费用:40×1200=48000元;
②由乙单独完成,需60天,
施工费用:60×850=51000元;
③由甲乙合作完成,需24天,
施工费用:24×(1200+850)=49200元;
∴由甲单独完成施工费用最低.
