2.4 二次函数的应用(第1课时) 课件 (共35张PPT)
文档属性
| 名称 | 2.4 二次函数的应用(第1课时) 课件 (共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
第二章 二次函数
2.4 二次函数的应用
第1课时 几何图形面积的最值
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、根据实际问题分析变量之间的关系,再由变量关系得到二次函数的关系式;
2、会利用二次函数的关系式,通过配方法求出实际问题的最大值或最小值,记住最值一定要符合实际问题的具体要求;
3、会利用二次函数求出图形几何问题中的面积最大值问题;
导入新课
观察与思考
已知一个矩形的长和宽的总和为20cm,求出这个矩形面积的最大值为多少?
设该矩形的长为xcm,则宽为(10-x)cm
则该图形的面积S=x(10-x)=-x2+10x
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
通过上面的说明,算出上题的答案.
讲授新课
知识点一 二次函数的最大值或最小值
典例精析
例1 写出下列抛物线的最值.
(1)y=x2-4x-5;
解:(1)∵a=1>0,对称轴为x=2,顶点坐标为(2,-9),
∴当x=2时,y取最小值,最小值为-9;
(2)y=-x2-3x+4.
(2)∵a=-1<0,对称轴为x= ,顶点坐标为( , ),
∴当x= 时,y取最大值,最大值为 ;
例2 已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为( )
A.3 B.-1 C.4 D.4或-1
解析:∵二次函数y=ax2+4x+a-1有最小值2,
∴a>0,y最小值= = =2,
整理,得a2-3a-4=0,解得a=-1或4.
∵a>0,∴a=4.故选C.
C
知识点二 几何图形面积的最大值
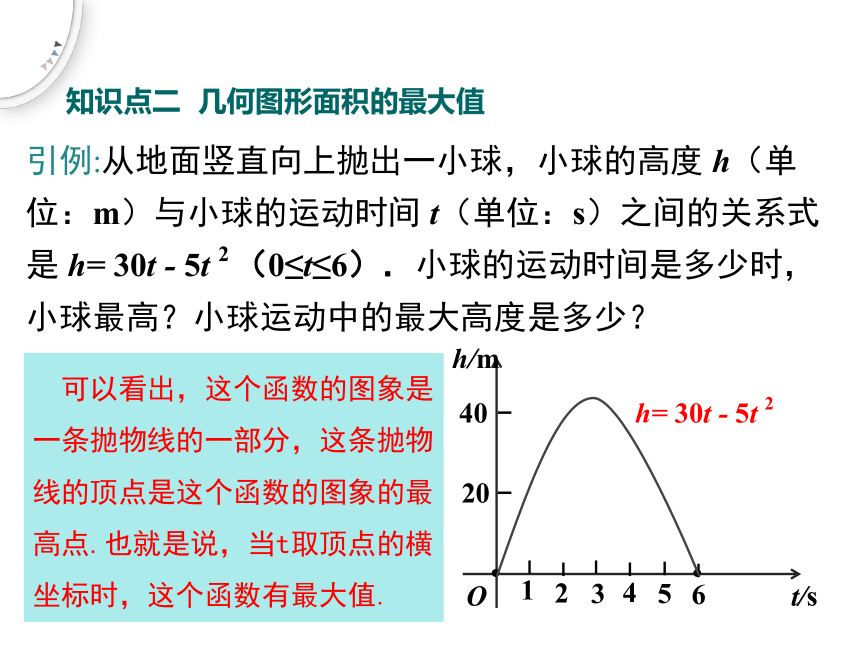
引例:从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点.也就是说,当t取顶点的横坐标时,这个函数有最大值.
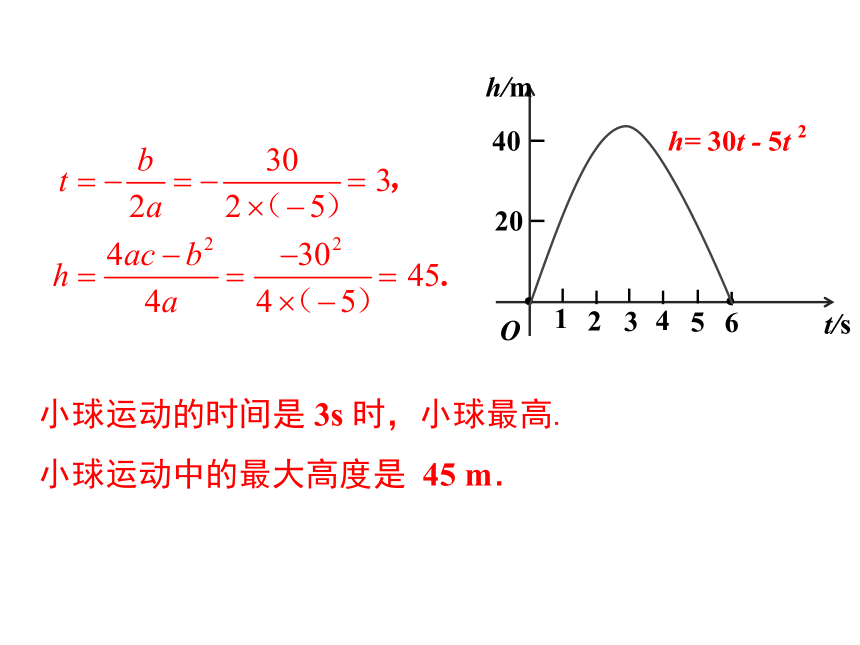
小球运动的时间是 3s 时,小球最高.小球运动中的最大高度是 45 m.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
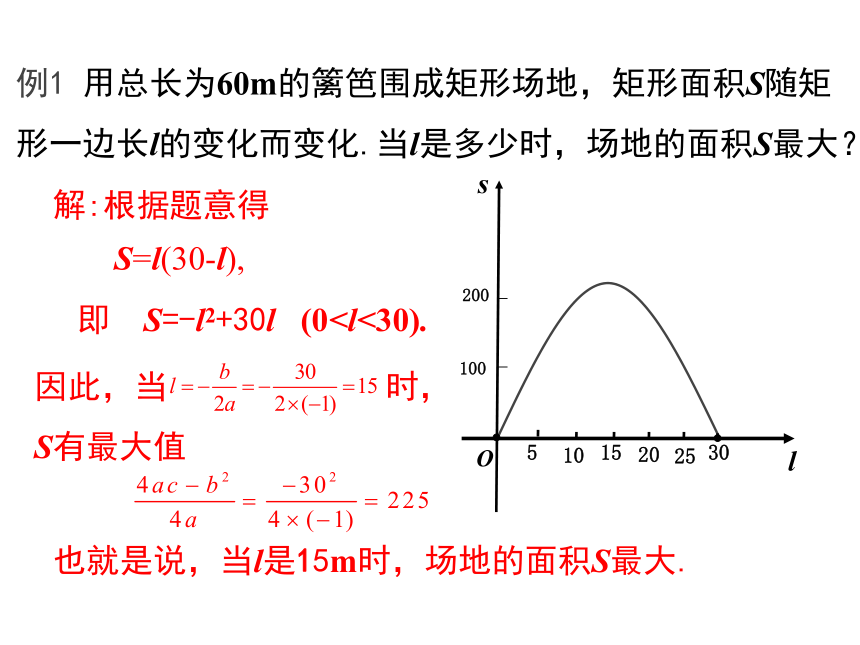
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
问题1 矩形面积公式是什么?
典例精析
问题2 如何用l表示另一边?
问题3 面积S的函数关系式是什么?
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
解:根据题意得
S=l(30-l),
即 S=-l2+30l (0因此,当 时,
S有最大值
也就是说,当l是15m时,场地的面积S最大.
5
10
15
20
25
30
100
200
l
s
O
知识要点
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
知识点三 利用二次函数解决拱桥问题
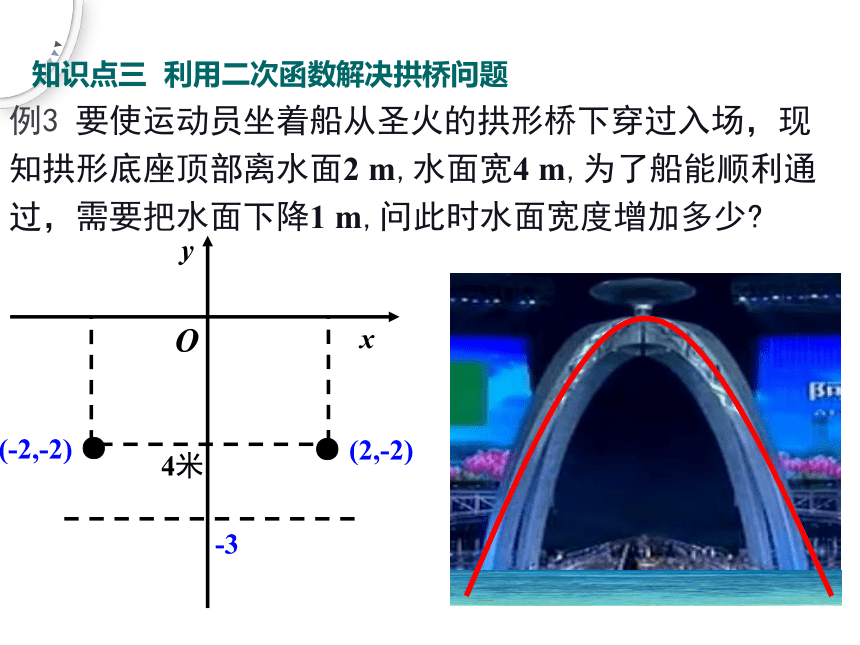
例3 要使运动员坐着船从圣火的拱形桥下穿过入场,现知拱形底座顶部离水面2 m,水面宽4 m,为了船能顺利通过,需要把水面下降1 m,问此时水面宽度增加多少
x
y
O
-3
(-2,-2) ●
● (2,-2)
4米
当 时,
所以,水面下降1m,水面的宽度为 m.
所以水面的宽度增加了 m.
解:建立如图所示坐标系,
由抛物线经过点(2,-2),可得
所以,这条抛物线的解析式为
当水面下降1m时,水面的纵坐标为
-3
x
y
O
(-2,-2) ●
● (2,-2)
设二次函数解析式为
知识要点
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
当堂练习
1.用总长为a米的材料做成如图1所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图2,则a的值是( )
A.16 B.12 C.8 D.4
【答案】B
【分析】因为x=2时,面积最大,为4,根据图形是矩形,由面积公式易得长为2米,从而得出a的值.
【详解】解:由图象可知,当x=2时,y有最大,最大值为4,
∴当x=2米,窗框的最大面积是4平方米,
根据矩形面积计算公式,矩形的长为4÷2=2(米),
∴材料总长a=2×3+2×3=12(米).
故选:B.
2.如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形的面积最大值是( )
A.16 B.32 C.36 D.64
【答案】B
【详解】解:设AC=x,四边形ABCD面积为S,则BD=16-x,
则:S=
当x=8时,S最大为:32﹔
故选:B.
3.把一根长4a的铁丝分成两段,每一段弯曲成一个正方形,面积和最小是( )
A. B.a2 C. D.
【答案】C
【详解】解:设其中的一段长为4x,面积和为y,则另一段长为4a-4x,且0<x<a,
面积和为y=x2+(a-x)2=2x2-2ax+a2=2(x-
∵2>0,开口向上,
∴x=时,y有最小值,为,
故选:C
4.如图,四边形ABCD中,AB=AD,CE⊥BD,CE=BD.若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
A.S= B.S=2x2-40x+200
C.S=x2-20x+100 D.S=x2+20x+100
【答案】C
【详解】解: ∵AB=AD,△ABD的周长为20cm,设AB=x
∴BD=20-x
∵CE=
∴CE=(20-2x)=10-x
∵CE⊥BD
S△BDC=x2-20x+100
故选:C
5.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=与y=-x2的图象,则阴影部分的面积是______.
答案:8
【详解】解:∵函数y=x2与y=-x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
∵正方形的边长为4,
∴S阴影部分=8.
故答案为:8.
6.用一根长为20米的绳子,围成一个矩形,设矩形一边长x米,则面积y=___________,围成的矩形的最大面积是__________m2.
【详解】解:设矩形的一边长为xm,则另一边长为:(10-x)m,
根据题意可得:y=x(10-x)=-x2+10x=-(x-5)2+25
∵ a=-1<0
当x=5时,函数最大值为25平方米.
故答案为:-x2+10x,25.
7.如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏(墙长9m),则这个围栏的最大面积为________ m2.
【答案】32
【详解】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(16-2x)m,
∴矩形围栏的面积为x(16-2x)=-2(x-4)2+32
∵ 墙长9m
∴16-2x≤9 即 x≥
∴当x=4时,矩形有最大面积为32m2,
故答案为:32.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
【详解】解:设花圃的宽AB为x米,面积为S平方米,
则S与x的之间的函数表达式为:S=(21-3x+3)x=-3x2+24x;
由题意可得:,
解得:.
故答案为:S=-3x2+24x,.
9.已知,一个铝合金窗框如图所示,所使用的铝合金材料长度为18cm.设AB长为xm,窗户的总面积为Sm2.
(1)求S关于x的函数表达式.
(2)若AB的长不能低于2m,且AB<BC,求此时窗户总面积S的最大值和最小值.
【答案】(1)S=-+9x
(2)窗户总面积S的最大值m2,最小值是12m2
【分析】(1)根据题意和图形可以求得S与x的函数表达式;
(2)根据题意可以得到关于x的不等式,从而求出x的范围,然后根据(1)中的函数解析式和二次函数的性质即可解答.
10.抛物线y=-3x2+mx+n经过点A(4,0),B(0,-4).
(1)求抛物线的解析式;
(2)在直线AB上方的抛物线上找一点C,使△ABC的面积最大,求C点坐标.
【答案】(1)y=-3x2+13x-4 ;(2)(2,10)
【分析】(1)已知抛物线y=-3x2+mx+n经过点A(4,0),B(0,-4),根据待定系数法列方程组即可求解;
(2)根据抛物线的图像,
设C(a,-3a2+13a-4),且点
C在抛物线上,求三角形ABC
的面积,找出相关点的
坐标即可求解.
课堂小结
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
拱桥问题
转化的关键
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
第二章 二次函数
2.4 二次函数的应用
第1课时 几何图形面积的最值
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、根据实际问题分析变量之间的关系,再由变量关系得到二次函数的关系式;
2、会利用二次函数的关系式,通过配方法求出实际问题的最大值或最小值,记住最值一定要符合实际问题的具体要求;
3、会利用二次函数求出图形几何问题中的面积最大值问题;
导入新课
观察与思考
已知一个矩形的长和宽的总和为20cm,求出这个矩形面积的最大值为多少?
设该矩形的长为xcm,则宽为(10-x)cm
则该图形的面积S=x(10-x)=-x2+10x
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
通过上面的说明,算出上题的答案.
讲授新课
知识点一 二次函数的最大值或最小值
典例精析
例1 写出下列抛物线的最值.
(1)y=x2-4x-5;
解:(1)∵a=1>0,对称轴为x=2,顶点坐标为(2,-9),
∴当x=2时,y取最小值,最小值为-9;
(2)y=-x2-3x+4.
(2)∵a=-1<0,对称轴为x= ,顶点坐标为( , ),
∴当x= 时,y取最大值,最大值为 ;
例2 已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为( )
A.3 B.-1 C.4 D.4或-1
解析:∵二次函数y=ax2+4x+a-1有最小值2,
∴a>0,y最小值= = =2,
整理,得a2-3a-4=0,解得a=-1或4.
∵a>0,∴a=4.故选C.
C
知识点二 几何图形面积的最大值
引例:从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点.也就是说,当t取顶点的横坐标时,这个函数有最大值.
小球运动的时间是 3s 时,小球最高.小球运动中的最大高度是 45 m.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
问题1 矩形面积公式是什么?
典例精析
问题2 如何用l表示另一边?
问题3 面积S的函数关系式是什么?
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
解:根据题意得
S=l(30-l),
即 S=-l2+30l (0
S有最大值
也就是说,当l是15m时,场地的面积S最大.
5
10
15
20
25
30
100
200
l
s
O
知识要点
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
知识点三 利用二次函数解决拱桥问题
例3 要使运动员坐着船从圣火的拱形桥下穿过入场,现知拱形底座顶部离水面2 m,水面宽4 m,为了船能顺利通过,需要把水面下降1 m,问此时水面宽度增加多少
x
y
O
-3
(-2,-2) ●
● (2,-2)
4米
当 时,
所以,水面下降1m,水面的宽度为 m.
所以水面的宽度增加了 m.
解:建立如图所示坐标系,
由抛物线经过点(2,-2),可得
所以,这条抛物线的解析式为
当水面下降1m时,水面的纵坐标为
-3
x
y
O
(-2,-2) ●
● (2,-2)
设二次函数解析式为
知识要点
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
当堂练习
1.用总长为a米的材料做成如图1所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图2,则a的值是( )
A.16 B.12 C.8 D.4
【答案】B
【分析】因为x=2时,面积最大,为4,根据图形是矩形,由面积公式易得长为2米,从而得出a的值.
【详解】解:由图象可知,当x=2时,y有最大,最大值为4,
∴当x=2米,窗框的最大面积是4平方米,
根据矩形面积计算公式,矩形的长为4÷2=2(米),
∴材料总长a=2×3+2×3=12(米).
故选:B.
2.如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形的面积最大值是( )
A.16 B.32 C.36 D.64
【答案】B
【详解】解:设AC=x,四边形ABCD面积为S,则BD=16-x,
则:S=
当x=8时,S最大为:32﹔
故选:B.
3.把一根长4a的铁丝分成两段,每一段弯曲成一个正方形,面积和最小是( )
A. B.a2 C. D.
【答案】C
【详解】解:设其中的一段长为4x,面积和为y,则另一段长为4a-4x,且0<x<a,
面积和为y=x2+(a-x)2=2x2-2ax+a2=2(x-
∵2>0,开口向上,
∴x=时,y有最小值,为,
故选:C
4.如图,四边形ABCD中,AB=AD,CE⊥BD,CE=BD.若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
A.S= B.S=2x2-40x+200
C.S=x2-20x+100 D.S=x2+20x+100
【答案】C
【详解】解: ∵AB=AD,△ABD的周长为20cm,设AB=x
∴BD=20-x
∵CE=
∴CE=(20-2x)=10-x
∵CE⊥BD
S△BDC=x2-20x+100
故选:C
5.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=与y=-x2的图象,则阴影部分的面积是______.
答案:8
【详解】解:∵函数y=x2与y=-x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
∵正方形的边长为4,
∴S阴影部分=8.
故答案为:8.
6.用一根长为20米的绳子,围成一个矩形,设矩形一边长x米,则面积y=___________,围成的矩形的最大面积是__________m2.
【详解】解:设矩形的一边长为xm,则另一边长为:(10-x)m,
根据题意可得:y=x(10-x)=-x2+10x=-(x-5)2+25
∵ a=-1<0
当x=5时,函数最大值为25平方米.
故答案为:-x2+10x,25.
7.如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏(墙长9m),则这个围栏的最大面积为________ m2.
【答案】32
【详解】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(16-2x)m,
∴矩形围栏的面积为x(16-2x)=-2(x-4)2+32
∵ 墙长9m
∴16-2x≤9 即 x≥
∴当x=4时,矩形有最大面积为32m2,
故答案为:32.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
【详解】解:设花圃的宽AB为x米,面积为S平方米,
则S与x的之间的函数表达式为:S=(21-3x+3)x=-3x2+24x;
由题意可得:,
解得:.
故答案为:S=-3x2+24x,.
9.已知,一个铝合金窗框如图所示,所使用的铝合金材料长度为18cm.设AB长为xm,窗户的总面积为Sm2.
(1)求S关于x的函数表达式.
(2)若AB的长不能低于2m,且AB<BC,求此时窗户总面积S的最大值和最小值.
【答案】(1)S=-+9x
(2)窗户总面积S的最大值m2,最小值是12m2
【分析】(1)根据题意和图形可以求得S与x的函数表达式;
(2)根据题意可以得到关于x的不等式,从而求出x的范围,然后根据(1)中的函数解析式和二次函数的性质即可解答.
10.抛物线y=-3x2+mx+n经过点A(4,0),B(0,-4).
(1)求抛物线的解析式;
(2)在直线AB上方的抛物线上找一点C,使△ABC的面积最大,求C点坐标.
【答案】(1)y=-3x2+13x-4 ;(2)(2,10)
【分析】(1)已知抛物线y=-3x2+mx+n经过点A(4,0),B(0,-4),根据待定系数法列方程组即可求解;
(2)根据抛物线的图像,
设C(a,-3a2+13a-4),且点
C在抛物线上,求三角形ABC
的面积,找出相关点的
坐标即可求解.
课堂小结
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
拱桥问题
转化的关键
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
