19.5.2 角的平分线同步练习题(含解析)
文档属性
| 名称 | 19.5.2 角的平分线同步练习题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 11:51:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.5角的平分线(第2课时)(原卷版)
【夯实基础】
一、单选题
1.(2019·上海民办永昌学校八年级阶段练习)如图,三条相互交叉的公路交于A、B、C三点,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址是△ABC的( )
A.三边高的交点 B.三边中垂线交点
C.三边中线交点 D.三内角平分线交点
二、填空题
2.(2019·上海民办永昌学校八年级阶段练习)△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形,则_______.
三、解答题
3.(2022·上海·八年级期末)如图,AD是△ADC中∠A的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF
4.(2020·上海市松江区民办茸一中学八年级阶段练习)如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
5.(2020·上海·同济大学附属实验中学八年级阶段练习)已知∠AOB,点M、N,在∠AOB的内部求作一点P,使点P到∠AOB的两边距离相等,且PM=PN
6.(2019·上海民办永昌学校八年级阶段练习)如图,已知∠MON及线段a,点G是射线ON上的点,求作:点P,使点P到OM、ON的距离相等,且PG=a。
7.(2018·上海普陀·八年级期末)如图所示,已知在△ABC中,∠C=90°,AC=6,AB=10.点D在边AC上,且点D到边AB和边BC的距离相等.
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求点D到边AB的距离.
8.(2019·上海外国语大学附属大境初级中学八年级阶段练习)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
9.(2022·上海·八年级单元测试)尺规作图.如图,已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(不写画图过程,保留作图痕迹)
【能力提升】
一、单选题
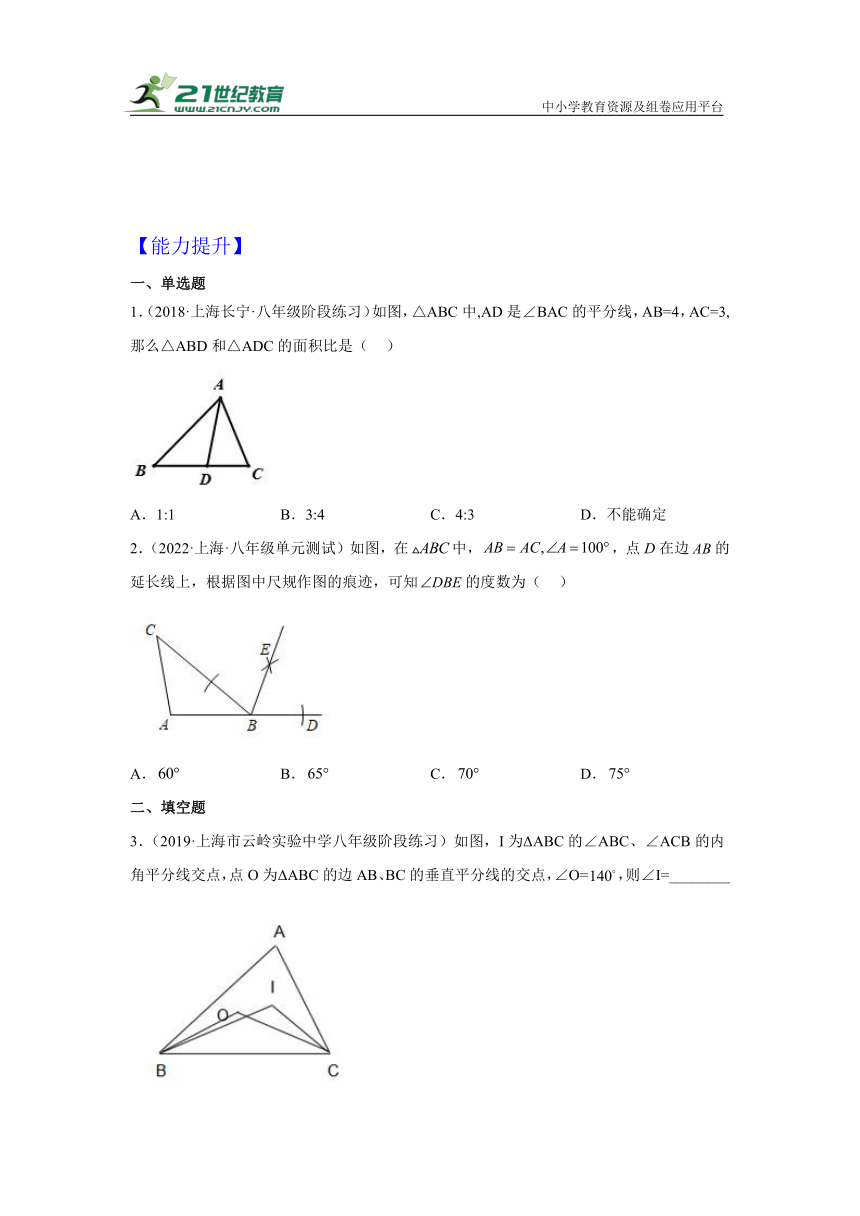
1.(2018·上海长宁·八年级阶段练习)如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
2.(2022·上海·八年级单元测试)如图,在中,,点D在边的延长线上,根据图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
二、填空题
3.(2019·上海市云岭实验中学八年级阶段练习)如图,I为ΔABC的∠ABC、∠ACB的内角平分线交点,点O为ΔABC的边AB、BC的垂直平分线的交点,∠O=,则∠I=________
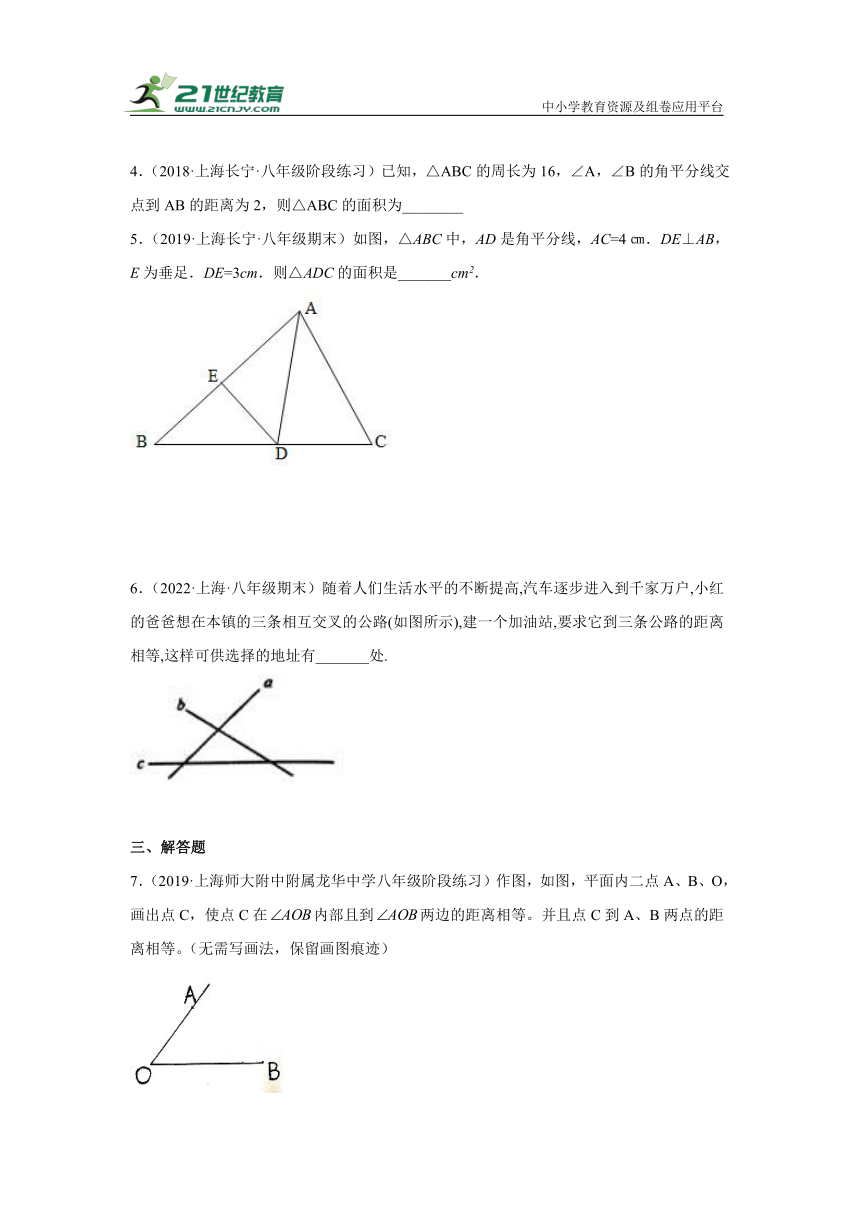
4.(2018·上海长宁·八年级阶段练习)已知,△ABC的周长为16,∠A,∠B的角平分线交点到AB的距离为2,则△ABC的面积为________
5.(2019·上海长宁·八年级期末)如图,△ABC中,AD是角平分线,AC=4㎝.DE⊥AB,E为垂足.DE=3cm.则△ADC的面积是_______cm2.
6.(2022·上海·八年级期末)随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
三、解答题
7.(2019·上海师大附中附属龙华中学八年级阶段练习)作图,如图,平面内二点A、B、O,画出点C,使点C在内部且到两边的距离相等。并且点C到A、B两点的距离相等。(无需写画法,保留画图痕迹)
8.(2018·上海浦东新·八年级期末)已知:如图,,平分,平分,交于点,于点,求证:点到与的距离相等.
9.(2022·上海·八年级单元测试)如图,在△ABC中,AC=6,BC=10.
(1)用尺规在AB边上求作点P,使点P到∠ACB两边的距离相等;
(不要求写出作法和证明,但要求保留作图痕迹,并写出结论)
(2)如果△ACP的面积为15,那么△BCP的面积是多少.
10.(2022·上海·八年级专题练习)作图:已知和线段r,请在内部作点P,使得点P到AC和BC的距离相等,并且点A到点P的距离等于定长r.(不写作法,保留痕迹)
11.(2019·上海市宜山中学八年级阶段练习)已知:∠AOB内一点C及线段(如图) ,求作:∠AOB内的点P,使P点到射线OA,OB的距离相等且PC= (不写作法但要保留作图痕迹,写出结论)
12.(2019·上海市进才中学北校八年级阶段练习)已知:∠AOB和直线a (如图) .求作:∠AOB内部一点P ,使点P到∠AOB的两边OA、OB以及直线a的距离均相等.
13.(2022·上海浦东新·八年级期末)如图,已知.
(1)根据要求作图:在边上求作一点,使得点到、的距离相等,在边上求作一点,使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:.
14.(2019·上海市毓秀学校八年级阶段练习)作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论.
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小.
15.(2022·上海·八年级单元测试)已知:∠O、点A及线段a(如图),求作:点P,使点P到∠O的两边的距离相等,且PA=a.(要求尺规作图,保留作图痕迹,不写作法).
16.(2021·上海·八年级专题练习)已知点是的平分线上一点,连接,.
(1)如图1,若,证明:
(2)如图2,若,,,证明:
(3)如图,若,点是的中点,当的最小时值为______
19.5角的平分线(第2课时)(解析版)
【夯实基础】
一、单选题
1.(2019·上海民办永昌学校八年级阶段练习)如图,三条相互交叉的公路交于A、B、C三点,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址是△ABC的( )
A.三边高的交点 B.三边中垂线交点
C.三边中线交点 D.三内角平分线交点
【答案】D
【分析】到三条公路的距离相等的点是△ABC的三内角平分线交点,外角角平分线的交点也可.
【详解】根据题意,得
到三条公路的距离相等的点是△ABC的三内角平分线交点
故答案为D.
【点睛】此题主要考查角平分线的性质,这是一道生活联系实际的题,熟练掌握,即可解题.
二、填空题
2.(2019·上海民办永昌学校八年级阶段练习)△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形,则_______.
【答案】
【分析】根据角平分线的性质得,三角形ABC分成的三个三角形有一条相等的高,故三个三角形的面积之比等于该高所对的边之比.
【详解】设边AB上的高为,边BC上的高为,边CA上的高为
由角平分线的性质得:
故
故答案为.
【点睛】本题考查了角平分线的性质(角平分线上的点到角两边的距离相等),掌握角平分线的性质是解题关键.
三、解答题
3.(2022·上海·八年级期末)如图,AD是△ADC中∠A的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF
【答案】见解析
【分析】由角平分线的性质可知,再利用三角形全等证明,根据线段垂直平分线的判定定理可得结论.
【详解】解:∵是中的平分线,,
∴,
∵,,
∴
∴点、D都在的垂直平分线上
∴
【点睛】本题综合考查了角平分线及线段的垂直平分线,熟练掌握角平分线的性质定理及线段垂直平分线的判定定理是解题的关键.
4.(2020·上海市松江区民办茸一中学八年级阶段练习)如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
【答案】见解析图
【分析】分别作∠AOB的角平分线以及线段EF的中垂线,两条线的交点即为所求.
【详解】如图所示,先作出∠AOB的角平分线OQ,根据角平分线的性质可知,在OQ上的所有点均满足到OA、OB的距离相等,
再作线段EF的中垂线MN,根据中垂线的性质可知,MN上的所有点均满足到E,F的距离相等,
此时OQ与MN 交点,既满足到OA、OB的距离相等,也满足到E,F的距离相等,即为所求的点P.
【点睛】本题考查角平分线及垂直平分线的画法及实际应用,理解它们的性质是解题关键.
5.(2020·上海·同济大学附属实验中学八年级阶段练习)已知∠AOB,点M、N,在∠AOB的内部求作一点P,使点P到∠AOB的两边距离相等,且PM=PN
【答案】见解析.
【分析】根据题意,点P到∠AOB的两边距离相等,即点P在∠AOB的角平分线上,又PM=PN,则点P在线段MN的垂直平分线上,据此作图即可.
【详解】作∠AOB的角平分线与线段MN的垂直平分线的交点,即为所求作的点P..
【点睛】本题考查尺规作图,其中涉及角平分线的画法、线段的垂直平分线的画法等知识,是基础考点,难度较易,掌握相关知识是解题关键.
6.(2019·上海民办永昌学校八年级阶段练习)如图,已知∠MON及线段a,点G是射线ON上的点,求作:点P,使点P到OM、ON的距离相等,且PG=a。
【答案】见解析
【分析】根据角平分线上的点到角的两边的距离相等可得点P在∠MON的平分线上,然后再以点G为圆心,以a的长度为半径画弧,与∠MON的平分线相交,交点就是所求的点P.
【详解】由题意,如图所示
【点睛】此题主要考查过直线上一点以及直线外一点作直线的垂线以及角平分线的性质,熟练掌握,即可解题.
7.(2018·上海普陀·八年级期末)如图所示,已知在△ABC中,∠C=90°,AC=6,AB=10.点D在边AC上,且点D到边AB和边BC的距离相等.
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求点D到边AB的距离.
【答案】(1)详见解析;(2)
【分析】(1)作∠ABC的角平分线交AC于D,则根据角平分线的性质可判断点D到边AB和边BC的距离相等;
(2)过点D作DE⊥AB于E,如图,利用勾股定理计算出BC=8,设DE=x,则DC=x,利用S△ADB+S△BCD=S△ABC得到x+x=×6×8,然后解方程求出x即可.
【详解】解:(1)如图,点D就是所要求作的点;
(2)过点D作DE⊥AB于E,如图,
在Rt△ABC中,BC= =8,
设DE=x,则DC=x,
∵S△ADB+S△BCD=S△ABC,
∴10x+8x=×6×8
∴x=,
∴点D到边AB的距离为.
【点睛】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了角平分线的性质.
8.(2019·上海外国语大学附属大境初级中学八年级阶段练习)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
【答案】答案见解析.
【分析】作的平分线交直线MN于P点.
【详解】解:根据题意,如图,作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,则点P即为所求.
9.(2022·上海·八年级单元测试)尺规作图.如图,已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(不写画图过程,保留作图痕迹)
【答案】作图详见解析.
【分析】因为点P满足PC=PD 所以点 P在线段CD的垂直平分线上, 又P到∠AOB两边的距离相等 ,所以点P在∠AOB或∠AOB补角的角平分线上.
【详解】解:根据题意作图,得
其中,点P和点P’即为所求
【能力提升】
一、单选题
1.(2018·上海长宁·八年级阶段练习)如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
【答案】C
【分析】如图,过D分别作DE⊥AB于E,DF⊥AC于F,根据角平分线的性质得到DE=DF,然后利用三角形的面积公式就可以得到△ABD与△ADC的面积比是AB:AC,再利用已知条件即可求出结果.
【详解】解:如图,过D分别作DE⊥AB于E,DF⊥AC于F,
∵AD是∠BAC的角平分线,
∴DE=DF,
∴S△ABD:S△ADC=AB DE:AC DF=AB:AC=4:3.
故选C.
【点睛】本题考查角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记等高三角形的面积关系是解题的关键.
2.(2022·上海·八年级单元测试)如图,在中,,点D在边的延长线上,根据图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
【答案】C
【分析】根据等边对等角先求解 再求解 结合尺规作图可得平分 从而可得答案.
【详解】解: ,
由作图可得:
由作图可得:是的角平分线,
故选C
【点睛】本题考查的是等腰三角形的性质,三角形内角和定理的应用,角平分线的作图,掌握“等腰三角形的等边对等角”是解本题的关键.
二、填空题
3.(2019·上海市云岭实验中学八年级阶段练习)如图,I为ΔABC的∠ABC、∠ACB的内角平分线交点,点O为ΔABC的边AB、BC的垂直平分线的交点,∠O=,则∠I=________
【答案】125°
【分析】利用基本结论:∠BOC=∠OBA+∠OCA+∠BAC,∠BEC=90°+∠BAC解决问题即可.
【详解】如图,连接OA.
∵点O是AB,AC的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOC=∠OBA+∠OAB+∠OCA+∠OAC=2∠BAC,
∵∠BOC=140°,
∴∠BAC=
∵点I是∠ABC、∠ACB角平分线的交点,
∴∠I=180°- (∠ABC+∠ACB)
=180°- (180°-∠BAC)
=90°+∠BAC,
=90°+35°
=125°,
故答案为:125°.
【点睛】本题考查三角形的内角和定理,线段的垂直平分线的性质,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
4.(2018·上海长宁·八年级阶段练习)已知,△ABC的周长为16,∠A,∠B的角平分线交点到AB的距离为2,则△ABC的面积为________
【答案】16
【分析】根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等,再根据三角形的面积公式列式计算即可得解.
【详解】解:设∠A和∠B的平分线相交于P,P到边AB的距离为2,
∴点P到AC、BC的距离为2,
∵△ABC的周长为16,
∴△ABC的面积=×AB×2+×BC×2+×AC×2=×(AB+BC+AC)×2=×16×2=16.
故答案为16.
【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并判断出点P到三角形三边的距离相等是解题的关键.
5.(2019·上海长宁·八年级期末)如图,△ABC中,AD是角平分线,AC=4㎝.DE⊥AB,E为垂足.DE=3cm.则△ADC的面积是_______cm2.
【答案】6
【分析】作辅助线,通过角平分线性质得DE=DF,再利用三角形面积公式即可求出△ADC的面积.
【详解】解:过点D作DF⊥AC与点F,如下图,
∵AD是角平分线, DE⊥AB,DE=3cm,
∴DE=DF=3,
又AC=4,
∴△ADC的面积= cm2.
【点睛】本题考查了三角形角平分线性质和三角形的面积,属于简单题,熟悉三角形角平分线的性质是解题关键.
6.(2022·上海·八年级期末)随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
【答案】4
【分析】分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
【详解】如图所示,
加油站站的地址有四处.
故选D.
【点睛】考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并是解题的关键,作出图形更形象直观.
三、解答题
7.(2019·上海师大附中附属龙华中学八年级阶段练习)作图,如图,平面内二点A、B、O,画出点C,使点C在内部且到两边的距离相等。并且点C到A、B两点的距离相等。(无需写画法,保留画图痕迹)
【答案】答案见解析
【分析】根据角平分线和线段垂直平分线的性质作图即可.
【详解】解:根据题意作出∠AOB的角平分线与线段AB的垂直平分线交于点C,点C即为所求.
【点睛】本题考查尺规作图,掌握角平分线和线段垂直平分线的性质是本题的解题关键.
8.(2018·上海浦东新·八年级期末)已知:如图,,平分,平分,交于点,于点,求证:点到与的距离相等.
【答案】见解析.
【分析】根据平行线的性质和角平分线的定义得到∠DOC=90°,进一步得到△CDO≌△CBO(ASA),得出DO=BO,则CE是BD的垂直平分线,根据等腰三角形的三线合一的性质得出EC平分∠BED,从而得证.
【详解】证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD==90°,
∴∠DOC=90°,
又CE平分∠BCD,
∴∠DCO=∠BCO,
∵CO=CO,∠COD=∠COB,
∴△CDO≌△CBO(ASA),
∴DO=BO,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
【点睛】本题考查的是平行线的性质、角平分线的性质,全等三角形的判定,等腰三角形的性质,掌握平行线的判定定理和性质定理是解题的关键.
9.(2022·上海·八年级单元测试)如图,在△ABC中,AC=6,BC=10.
(1)用尺规在AB边上求作点P,使点P到∠ACB两边的距离相等;
(不要求写出作法和证明,但要求保留作图痕迹,并写出结论)
(2)如果△ACP的面积为15,那么△BCP的面积是多少.
【答案】(1)见解析
(2)25
【分析】(1)作∠ACB的角平分线与AB的交点即为点P;
(2)如图:过点P作PE⊥CA延长线于点E,PF⊥BC于点F,然后证得,最后代入计算即可.
(1)
解:如图:点P即为所求;
(2)
解:如图:过点P作PE⊥CA延长线于点E,PF⊥BC于点F
∵CP平分∠ACB,
∴PE=PF,
∴
∵=15
∴
∴=25.
【点睛】本题主要考查了作角平分线、角平分线的性质定理等知识点,解题的关键是灵活运用角平分线的性质.
10.(2022·上海·八年级专题练习)作图:已知和线段r,请在内部作点P,使得点P到AC和BC的距离相等,并且点A到点P的距离等于定长r.(不写作法,保留痕迹)
【答案】图见解析.
【分析】根据题意点P到AC和BC的距离相等,可知点P在的角平分线上,点A到点P的距离等于定长r,可知点P在以点A为圆心,以定长r为半径的圆上,由此作图即可.
【详解】如图,先作的角平分线,再以点A为圆心,以定长r为半径作圆弧,圆弧与角平分线的交点即为点P.
【点睛】本题主要考查角平分线的画法,属于基础题,需要有一定的画图能力,熟练掌握角平分线的画法是解题的关键.
11.(2019·上海市宜山中学八年级阶段练习)已知:∠AOB内一点C及线段(如图) ,求作:∠AOB内的点P,使P点到射线OA,OB的距离相等且PC= (不写作法但要保留作图痕迹,写出结论)
【答案】答案见解析.
【分析】根据角平分线的性质做∠AOB的角平分线,然后以点C为圆心,线段a为半径画圆,与角平分线的交点即为所求.
【详解】解:如图即为所求:
【点睛】本题考查尺规作图及截取线段,正确作图是本题的解题关键.
12.(2019·上海市进才中学北校八年级阶段练习)已知:∠AOB和直线a (如图) .求作:∠AOB内部一点P ,使点P到∠AOB的两边OA、OB以及直线a的距离均相等.
【答案】见解析
【分析】作∠AOB的角平分线,作射线OB与直线a所夹角的角平分线,两平分线的交点即为P点.
【详解】如图,P为所求.
【点睛】此题主要考查角平分线的作图,解题的关键是熟知角平分线的性质.
13.(2022·上海浦东新·八年级期末)如图,已知.
(1)根据要求作图:在边上求作一点,使得点到、的距离相等,在边上求作一点,使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:.
【答案】(1)作图见解析;(2)证明见解析.
【分析】(1)到、的距离相等,则点D在的角平分线上,作的角平分线与BC的交点即为点D;到点、的距离相等,则点E在AD的垂直平分线上,作AD的垂直平分线与AB的交点即为点E;
(2)根据角平分线的性质和线段垂直平分线的性质可得∠CAD=∠ADE,再根据平行线的判定即可求解.
【详解】(1)解:如图所示:
(2)证明:∵AD是∠BAC的角平分线,
∴∠CAD=∠BAD,
∵EF是AD的中垂线,
∴ED=EA,
∴∠ADE=∠BAD,
∴∠CAD=∠ADE,
∴DE∥AC.
【点睛】本题考查了角平分线的性质、垂直平分线的性质、等腰三角形的定义和性质、以及两条直线平行的判定定理,判定直线平行的常用方法有:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行.
14.(2019·上海市毓秀学校八年级阶段练习)作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论.
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小.
【答案】(1)见解析;(2)见解析
【分析】(1)分别作出∠AOB的角平分线及线段CD的垂直平分线,两条直线的交点即为所求P点;
(2)先作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求.
【详解】解:(1)以O为圆心,以任意长为半径画圆,分别交OA,OB于E、F两点,再分别以E、F为圆心,以大于EF为半径画圆,两圆相交于G点,连接OG;
连接CD,分别以C、D为圆心,以大于CD为半径画圆,两圆相交于H、I两点,连接HI,直线HI于射线OG相交于P点,
则点P即为所求;
(2)如图,作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求;
.
【点睛】本题考查作图-应用与设计作图,熟知轴对称的性质,角的平分线和线段的垂直平分线的性质是解题的关键.
15.(2022·上海·八年级单元测试)已知:∠O、点A及线段a(如图),求作:点P,使点P到∠O的两边的距离相等,且PA=a.(要求尺规作图,保留作图痕迹,不写作法).
【答案】答案见解析.
【分析】先利用尺规作图作出∠O的平分线,再以点A为圆心,线段a的长度为半径画弧,与角平分线的交点即为所求.
【详解】解:如图所示,点P1和点P2即为所求.
【点睛】考查作图-复杂作图,解题的关键是熟练掌握角平分线的尺规作图和角平分线的性质.
16.(2021·上海·八年级专题练习)已知点是的平分线上一点,连接,.
(1)如图1,若,证明:
(2)如图2,若,,,证明:
(3)如图,若,点是的中点,当的最小时值为______.
【答案】(1)见解析;(2)见解析;(3)
【分析】(1)要求证,根据全等三角形的判定证明即可;
(2)根据等腰三角形的性质以及角平分线的性质可得出,可得:,要证,继续做辅助线求证三角形全等,即可求解;
(3)根据可知是等边三角形,由题意的最小时,即BE为直线时,根据正三角形重心的性质求解.
【详解】(1)证明:∵平分
∴
∴在和中
∴(SAS)
∴
(2)令,
∵
∴
∵
∴
∵平分
∴
即
∴,
在
作于
连
∵有等腰
∴平分
∴,
∵∴
∴在中,
中,
∴
∴平分
作延长线于,∴
∴在中,
∵
∴
在中
∴在和中
∴
∴
成立得证.
(3)∵,
∴是等边三角形,
∵AP是的平分线,
∴延长AP交BC于点D,则AD是BC垂直平分线,
∴,
∴最小即为最小,
∴BE为一条线段时最小,
∵BE、AD是的中线交于点P,
∴P为的重心,
∴,即.
.
【点睛】本题主要考查的是等边三角形的性质,全等三角形的判定,三角形重心的性质以及角平分线的性质,熟练掌握全等三角形的性质,三角形重心以及等边三角形的性质是解决本题的关键。
19.5角的平分线(第2课时)(原卷版)
【夯实基础】
一、单选题
1.(2019·上海民办永昌学校八年级阶段练习)如图,三条相互交叉的公路交于A、B、C三点,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址是△ABC的( )
A.三边高的交点 B.三边中垂线交点
C.三边中线交点 D.三内角平分线交点
二、填空题
2.(2019·上海民办永昌学校八年级阶段练习)△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形,则_______.
三、解答题
3.(2022·上海·八年级期末)如图,AD是△ADC中∠A的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF
4.(2020·上海市松江区民办茸一中学八年级阶段练习)如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
5.(2020·上海·同济大学附属实验中学八年级阶段练习)已知∠AOB,点M、N,在∠AOB的内部求作一点P,使点P到∠AOB的两边距离相等,且PM=PN
6.(2019·上海民办永昌学校八年级阶段练习)如图,已知∠MON及线段a,点G是射线ON上的点,求作:点P,使点P到OM、ON的距离相等,且PG=a。
7.(2018·上海普陀·八年级期末)如图所示,已知在△ABC中,∠C=90°,AC=6,AB=10.点D在边AC上,且点D到边AB和边BC的距离相等.
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求点D到边AB的距离.
8.(2019·上海外国语大学附属大境初级中学八年级阶段练习)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
9.(2022·上海·八年级单元测试)尺规作图.如图,已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(不写画图过程,保留作图痕迹)
【能力提升】
一、单选题
1.(2018·上海长宁·八年级阶段练习)如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
2.(2022·上海·八年级单元测试)如图,在中,,点D在边的延长线上,根据图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
二、填空题
3.(2019·上海市云岭实验中学八年级阶段练习)如图,I为ΔABC的∠ABC、∠ACB的内角平分线交点,点O为ΔABC的边AB、BC的垂直平分线的交点,∠O=,则∠I=________
4.(2018·上海长宁·八年级阶段练习)已知,△ABC的周长为16,∠A,∠B的角平分线交点到AB的距离为2,则△ABC的面积为________
5.(2019·上海长宁·八年级期末)如图,△ABC中,AD是角平分线,AC=4㎝.DE⊥AB,E为垂足.DE=3cm.则△ADC的面积是_______cm2.
6.(2022·上海·八年级期末)随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
三、解答题
7.(2019·上海师大附中附属龙华中学八年级阶段练习)作图,如图,平面内二点A、B、O,画出点C,使点C在内部且到两边的距离相等。并且点C到A、B两点的距离相等。(无需写画法,保留画图痕迹)
8.(2018·上海浦东新·八年级期末)已知:如图,,平分,平分,交于点,于点,求证:点到与的距离相等.
9.(2022·上海·八年级单元测试)如图,在△ABC中,AC=6,BC=10.
(1)用尺规在AB边上求作点P,使点P到∠ACB两边的距离相等;
(不要求写出作法和证明,但要求保留作图痕迹,并写出结论)
(2)如果△ACP的面积为15,那么△BCP的面积是多少.
10.(2022·上海·八年级专题练习)作图:已知和线段r,请在内部作点P,使得点P到AC和BC的距离相等,并且点A到点P的距离等于定长r.(不写作法,保留痕迹)
11.(2019·上海市宜山中学八年级阶段练习)已知:∠AOB内一点C及线段(如图) ,求作:∠AOB内的点P,使P点到射线OA,OB的距离相等且PC= (不写作法但要保留作图痕迹,写出结论)
12.(2019·上海市进才中学北校八年级阶段练习)已知:∠AOB和直线a (如图) .求作:∠AOB内部一点P ,使点P到∠AOB的两边OA、OB以及直线a的距离均相等.
13.(2022·上海浦东新·八年级期末)如图,已知.
(1)根据要求作图:在边上求作一点,使得点到、的距离相等,在边上求作一点,使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:.
14.(2019·上海市毓秀学校八年级阶段练习)作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论.
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小.
15.(2022·上海·八年级单元测试)已知:∠O、点A及线段a(如图),求作:点P,使点P到∠O的两边的距离相等,且PA=a.(要求尺规作图,保留作图痕迹,不写作法).
16.(2021·上海·八年级专题练习)已知点是的平分线上一点,连接,.
(1)如图1,若,证明:
(2)如图2,若,,,证明:
(3)如图,若,点是的中点,当的最小时值为______
19.5角的平分线(第2课时)(解析版)
【夯实基础】
一、单选题
1.(2019·上海民办永昌学校八年级阶段练习)如图,三条相互交叉的公路交于A、B、C三点,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址是△ABC的( )
A.三边高的交点 B.三边中垂线交点
C.三边中线交点 D.三内角平分线交点
【答案】D
【分析】到三条公路的距离相等的点是△ABC的三内角平分线交点,外角角平分线的交点也可.
【详解】根据题意,得
到三条公路的距离相等的点是△ABC的三内角平分线交点
故答案为D.
【点睛】此题主要考查角平分线的性质,这是一道生活联系实际的题,熟练掌握,即可解题.
二、填空题
2.(2019·上海民办永昌学校八年级阶段练习)△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形,则_______.
【答案】
【分析】根据角平分线的性质得,三角形ABC分成的三个三角形有一条相等的高,故三个三角形的面积之比等于该高所对的边之比.
【详解】设边AB上的高为,边BC上的高为,边CA上的高为
由角平分线的性质得:
故
故答案为.
【点睛】本题考查了角平分线的性质(角平分线上的点到角两边的距离相等),掌握角平分线的性质是解题关键.
三、解答题
3.(2022·上海·八年级期末)如图,AD是△ADC中∠A的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF
【答案】见解析
【分析】由角平分线的性质可知,再利用三角形全等证明,根据线段垂直平分线的判定定理可得结论.
【详解】解:∵是中的平分线,,
∴,
∵,,
∴
∴点、D都在的垂直平分线上
∴
【点睛】本题综合考查了角平分线及线段的垂直平分线,熟练掌握角平分线的性质定理及线段垂直平分线的判定定理是解题的关键.
4.(2020·上海市松江区民办茸一中学八年级阶段练习)如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
【答案】见解析图
【分析】分别作∠AOB的角平分线以及线段EF的中垂线,两条线的交点即为所求.
【详解】如图所示,先作出∠AOB的角平分线OQ,根据角平分线的性质可知,在OQ上的所有点均满足到OA、OB的距离相等,
再作线段EF的中垂线MN,根据中垂线的性质可知,MN上的所有点均满足到E,F的距离相等,
此时OQ与MN 交点,既满足到OA、OB的距离相等,也满足到E,F的距离相等,即为所求的点P.
【点睛】本题考查角平分线及垂直平分线的画法及实际应用,理解它们的性质是解题关键.
5.(2020·上海·同济大学附属实验中学八年级阶段练习)已知∠AOB,点M、N,在∠AOB的内部求作一点P,使点P到∠AOB的两边距离相等,且PM=PN
【答案】见解析.
【分析】根据题意,点P到∠AOB的两边距离相等,即点P在∠AOB的角平分线上,又PM=PN,则点P在线段MN的垂直平分线上,据此作图即可.
【详解】作∠AOB的角平分线与线段MN的垂直平分线的交点,即为所求作的点P..
【点睛】本题考查尺规作图,其中涉及角平分线的画法、线段的垂直平分线的画法等知识,是基础考点,难度较易,掌握相关知识是解题关键.
6.(2019·上海民办永昌学校八年级阶段练习)如图,已知∠MON及线段a,点G是射线ON上的点,求作:点P,使点P到OM、ON的距离相等,且PG=a。
【答案】见解析
【分析】根据角平分线上的点到角的两边的距离相等可得点P在∠MON的平分线上,然后再以点G为圆心,以a的长度为半径画弧,与∠MON的平分线相交,交点就是所求的点P.
【详解】由题意,如图所示
【点睛】此题主要考查过直线上一点以及直线外一点作直线的垂线以及角平分线的性质,熟练掌握,即可解题.
7.(2018·上海普陀·八年级期末)如图所示,已知在△ABC中,∠C=90°,AC=6,AB=10.点D在边AC上,且点D到边AB和边BC的距离相等.
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求点D到边AB的距离.
【答案】(1)详见解析;(2)
【分析】(1)作∠ABC的角平分线交AC于D,则根据角平分线的性质可判断点D到边AB和边BC的距离相等;
(2)过点D作DE⊥AB于E,如图,利用勾股定理计算出BC=8,设DE=x,则DC=x,利用S△ADB+S△BCD=S△ABC得到x+x=×6×8,然后解方程求出x即可.
【详解】解:(1)如图,点D就是所要求作的点;
(2)过点D作DE⊥AB于E,如图,
在Rt△ABC中,BC= =8,
设DE=x,则DC=x,
∵S△ADB+S△BCD=S△ABC,
∴10x+8x=×6×8
∴x=,
∴点D到边AB的距离为.
【点睛】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了角平分线的性质.
8.(2019·上海外国语大学附属大境初级中学八年级阶段练习)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
【答案】答案见解析.
【分析】作的平分线交直线MN于P点.
【详解】解:根据题意,如图,作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,则点P即为所求.
9.(2022·上海·八年级单元测试)尺规作图.如图,已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(不写画图过程,保留作图痕迹)
【答案】作图详见解析.
【分析】因为点P满足PC=PD 所以点 P在线段CD的垂直平分线上, 又P到∠AOB两边的距离相等 ,所以点P在∠AOB或∠AOB补角的角平分线上.
【详解】解:根据题意作图,得
其中,点P和点P’即为所求
【能力提升】
一、单选题
1.(2018·上海长宁·八年级阶段练习)如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
【答案】C
【分析】如图,过D分别作DE⊥AB于E,DF⊥AC于F,根据角平分线的性质得到DE=DF,然后利用三角形的面积公式就可以得到△ABD与△ADC的面积比是AB:AC,再利用已知条件即可求出结果.
【详解】解:如图,过D分别作DE⊥AB于E,DF⊥AC于F,
∵AD是∠BAC的角平分线,
∴DE=DF,
∴S△ABD:S△ADC=AB DE:AC DF=AB:AC=4:3.
故选C.
【点睛】本题考查角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记等高三角形的面积关系是解题的关键.
2.(2022·上海·八年级单元测试)如图,在中,,点D在边的延长线上,根据图中尺规作图的痕迹,可知的度数为( )
A. B. C. D.
【答案】C
【分析】根据等边对等角先求解 再求解 结合尺规作图可得平分 从而可得答案.
【详解】解: ,
由作图可得:
由作图可得:是的角平分线,
故选C
【点睛】本题考查的是等腰三角形的性质,三角形内角和定理的应用,角平分线的作图,掌握“等腰三角形的等边对等角”是解本题的关键.
二、填空题
3.(2019·上海市云岭实验中学八年级阶段练习)如图,I为ΔABC的∠ABC、∠ACB的内角平分线交点,点O为ΔABC的边AB、BC的垂直平分线的交点,∠O=,则∠I=________
【答案】125°
【分析】利用基本结论:∠BOC=∠OBA+∠OCA+∠BAC,∠BEC=90°+∠BAC解决问题即可.
【详解】如图,连接OA.
∵点O是AB,AC的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOC=∠OBA+∠OAB+∠OCA+∠OAC=2∠BAC,
∵∠BOC=140°,
∴∠BAC=
∵点I是∠ABC、∠ACB角平分线的交点,
∴∠I=180°- (∠ABC+∠ACB)
=180°- (180°-∠BAC)
=90°+∠BAC,
=90°+35°
=125°,
故答案为:125°.
【点睛】本题考查三角形的内角和定理,线段的垂直平分线的性质,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
4.(2018·上海长宁·八年级阶段练习)已知,△ABC的周长为16,∠A,∠B的角平分线交点到AB的距离为2,则△ABC的面积为________
【答案】16
【分析】根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等,再根据三角形的面积公式列式计算即可得解.
【详解】解:设∠A和∠B的平分线相交于P,P到边AB的距离为2,
∴点P到AC、BC的距离为2,
∵△ABC的周长为16,
∴△ABC的面积=×AB×2+×BC×2+×AC×2=×(AB+BC+AC)×2=×16×2=16.
故答案为16.
【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并判断出点P到三角形三边的距离相等是解题的关键.
5.(2019·上海长宁·八年级期末)如图,△ABC中,AD是角平分线,AC=4㎝.DE⊥AB,E为垂足.DE=3cm.则△ADC的面积是_______cm2.
【答案】6
【分析】作辅助线,通过角平分线性质得DE=DF,再利用三角形面积公式即可求出△ADC的面积.
【详解】解:过点D作DF⊥AC与点F,如下图,
∵AD是角平分线, DE⊥AB,DE=3cm,
∴DE=DF=3,
又AC=4,
∴△ADC的面积= cm2.
【点睛】本题考查了三角形角平分线性质和三角形的面积,属于简单题,熟悉三角形角平分线的性质是解题关键.
6.(2022·上海·八年级期末)随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
【答案】4
【分析】分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
【详解】如图所示,
加油站站的地址有四处.
故选D.
【点睛】考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并是解题的关键,作出图形更形象直观.
三、解答题
7.(2019·上海师大附中附属龙华中学八年级阶段练习)作图,如图,平面内二点A、B、O,画出点C,使点C在内部且到两边的距离相等。并且点C到A、B两点的距离相等。(无需写画法,保留画图痕迹)
【答案】答案见解析
【分析】根据角平分线和线段垂直平分线的性质作图即可.
【详解】解:根据题意作出∠AOB的角平分线与线段AB的垂直平分线交于点C,点C即为所求.
【点睛】本题考查尺规作图,掌握角平分线和线段垂直平分线的性质是本题的解题关键.
8.(2018·上海浦东新·八年级期末)已知:如图,,平分,平分,交于点,于点,求证:点到与的距离相等.
【答案】见解析.
【分析】根据平行线的性质和角平分线的定义得到∠DOC=90°,进一步得到△CDO≌△CBO(ASA),得出DO=BO,则CE是BD的垂直平分线,根据等腰三角形的三线合一的性质得出EC平分∠BED,从而得证.
【详解】证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD==90°,
∴∠DOC=90°,
又CE平分∠BCD,
∴∠DCO=∠BCO,
∵CO=CO,∠COD=∠COB,
∴△CDO≌△CBO(ASA),
∴DO=BO,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
【点睛】本题考查的是平行线的性质、角平分线的性质,全等三角形的判定,等腰三角形的性质,掌握平行线的判定定理和性质定理是解题的关键.
9.(2022·上海·八年级单元测试)如图,在△ABC中,AC=6,BC=10.
(1)用尺规在AB边上求作点P,使点P到∠ACB两边的距离相等;
(不要求写出作法和证明,但要求保留作图痕迹,并写出结论)
(2)如果△ACP的面积为15,那么△BCP的面积是多少.
【答案】(1)见解析
(2)25
【分析】(1)作∠ACB的角平分线与AB的交点即为点P;
(2)如图:过点P作PE⊥CA延长线于点E,PF⊥BC于点F,然后证得,最后代入计算即可.
(1)
解:如图:点P即为所求;
(2)
解:如图:过点P作PE⊥CA延长线于点E,PF⊥BC于点F
∵CP平分∠ACB,
∴PE=PF,
∴
∵=15
∴
∴=25.
【点睛】本题主要考查了作角平分线、角平分线的性质定理等知识点,解题的关键是灵活运用角平分线的性质.
10.(2022·上海·八年级专题练习)作图:已知和线段r,请在内部作点P,使得点P到AC和BC的距离相等,并且点A到点P的距离等于定长r.(不写作法,保留痕迹)
【答案】图见解析.
【分析】根据题意点P到AC和BC的距离相等,可知点P在的角平分线上,点A到点P的距离等于定长r,可知点P在以点A为圆心,以定长r为半径的圆上,由此作图即可.
【详解】如图,先作的角平分线,再以点A为圆心,以定长r为半径作圆弧,圆弧与角平分线的交点即为点P.
【点睛】本题主要考查角平分线的画法,属于基础题,需要有一定的画图能力,熟练掌握角平分线的画法是解题的关键.
11.(2019·上海市宜山中学八年级阶段练习)已知:∠AOB内一点C及线段(如图) ,求作:∠AOB内的点P,使P点到射线OA,OB的距离相等且PC= (不写作法但要保留作图痕迹,写出结论)
【答案】答案见解析.
【分析】根据角平分线的性质做∠AOB的角平分线,然后以点C为圆心,线段a为半径画圆,与角平分线的交点即为所求.
【详解】解:如图即为所求:
【点睛】本题考查尺规作图及截取线段,正确作图是本题的解题关键.
12.(2019·上海市进才中学北校八年级阶段练习)已知:∠AOB和直线a (如图) .求作:∠AOB内部一点P ,使点P到∠AOB的两边OA、OB以及直线a的距离均相等.
【答案】见解析
【分析】作∠AOB的角平分线,作射线OB与直线a所夹角的角平分线,两平分线的交点即为P点.
【详解】如图,P为所求.
【点睛】此题主要考查角平分线的作图,解题的关键是熟知角平分线的性质.
13.(2022·上海浦东新·八年级期末)如图,已知.
(1)根据要求作图:在边上求作一点,使得点到、的距离相等,在边上求作一点,使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:.
【答案】(1)作图见解析;(2)证明见解析.
【分析】(1)到、的距离相等,则点D在的角平分线上,作的角平分线与BC的交点即为点D;到点、的距离相等,则点E在AD的垂直平分线上,作AD的垂直平分线与AB的交点即为点E;
(2)根据角平分线的性质和线段垂直平分线的性质可得∠CAD=∠ADE,再根据平行线的判定即可求解.
【详解】(1)解:如图所示:
(2)证明:∵AD是∠BAC的角平分线,
∴∠CAD=∠BAD,
∵EF是AD的中垂线,
∴ED=EA,
∴∠ADE=∠BAD,
∴∠CAD=∠ADE,
∴DE∥AC.
【点睛】本题考查了角平分线的性质、垂直平分线的性质、等腰三角形的定义和性质、以及两条直线平行的判定定理,判定直线平行的常用方法有:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行.
14.(2019·上海市毓秀学校八年级阶段练习)作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论.
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小.
【答案】(1)见解析;(2)见解析
【分析】(1)分别作出∠AOB的角平分线及线段CD的垂直平分线,两条直线的交点即为所求P点;
(2)先作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求.
【详解】解:(1)以O为圆心,以任意长为半径画圆,分别交OA,OB于E、F两点,再分别以E、F为圆心,以大于EF为半径画圆,两圆相交于G点,连接OG;
连接CD,分别以C、D为圆心,以大于CD为半径画圆,两圆相交于H、I两点,连接HI,直线HI于射线OG相交于P点,
则点P即为所求;
(2)如图,作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求;
.
【点睛】本题考查作图-应用与设计作图,熟知轴对称的性质,角的平分线和线段的垂直平分线的性质是解题的关键.
15.(2022·上海·八年级单元测试)已知:∠O、点A及线段a(如图),求作:点P,使点P到∠O的两边的距离相等,且PA=a.(要求尺规作图,保留作图痕迹,不写作法).
【答案】答案见解析.
【分析】先利用尺规作图作出∠O的平分线,再以点A为圆心,线段a的长度为半径画弧,与角平分线的交点即为所求.
【详解】解:如图所示,点P1和点P2即为所求.
【点睛】考查作图-复杂作图,解题的关键是熟练掌握角平分线的尺规作图和角平分线的性质.
16.(2021·上海·八年级专题练习)已知点是的平分线上一点,连接,.
(1)如图1,若,证明:
(2)如图2,若,,,证明:
(3)如图,若,点是的中点,当的最小时值为______.
【答案】(1)见解析;(2)见解析;(3)
【分析】(1)要求证,根据全等三角形的判定证明即可;
(2)根据等腰三角形的性质以及角平分线的性质可得出,可得:,要证,继续做辅助线求证三角形全等,即可求解;
(3)根据可知是等边三角形,由题意的最小时,即BE为直线时,根据正三角形重心的性质求解.
【详解】(1)证明:∵平分
∴
∴在和中
∴(SAS)
∴
(2)令,
∵
∴
∵
∴
∵平分
∴
即
∴,
在
作于
连
∵有等腰
∴平分
∴,
∵∴
∴在中,
中,
∴
∴平分
作延长线于,∴
∴在中,
∵
∴
在中
∴在和中
∴
∴
成立得证.
(3)∵,
∴是等边三角形,
∵AP是的平分线,
∴延长AP交BC于点D,则AD是BC垂直平分线,
∴,
∴最小即为最小,
∴BE为一条线段时最小,
∵BE、AD是的中线交于点P,
∴P为的重心,
∴,即.
.
【点睛】本题主要考查的是等边三角形的性质,全等三角形的判定,三角形重心的性质以及角平分线的性质,熟练掌握全等三角形的性质,三角形重心以及等边三角形的性质是解决本题的关键。
