第五章 一元一次方程 单元小结 课件 (共25张PPT)
文档属性
| 名称 | 第五章 一元一次方程 单元小结 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:18:57 | ||
图片预览








文档简介
(共25张PPT)
新课标 北师大版
七年级上册
第五章
一元一次方程
单元小结
中小学教育资源及组卷应用平台
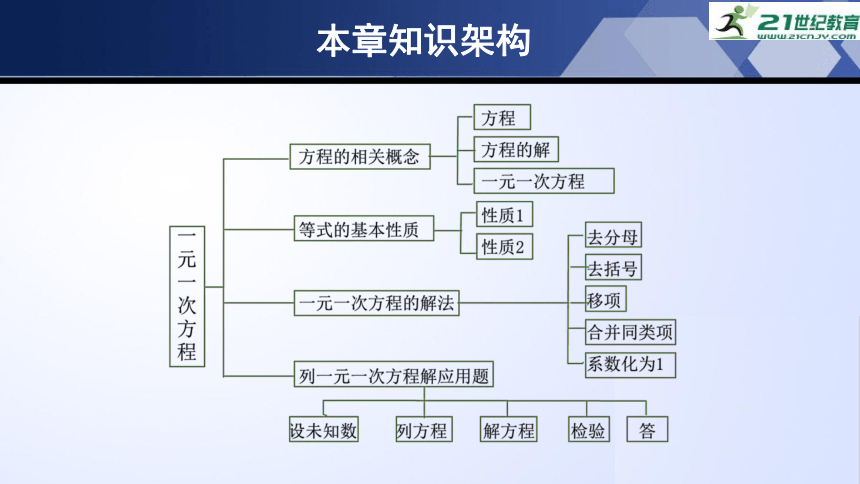
本章知识架构
知识专题
1. 方程的定义
方程的定义:含有______________ 的等式叫做方程.
在这一概念中要抓住方程定义的两个要点:①是______________ ;②含有______________ .
2. 等式的基本性质:
(1)等式的性质
性质1:等式两边同时加(或减)同一个代数式,所得结果仍是______________ ;
未知数
等式
未知数
等式
知识专题
性质2:等式两边同时乘同一个数(或______________ 一个不为零的数),所得结果仍是等式. 此外,等式还具有对称性和传递性,即:
①对称性:如果a=b,那么b=a,即等式的左、右两边交换位置,所得结果仍是等式.
②传递性:如果a=b,且b=c,那么a=c,这一性质也叫做等量代换.
(2)利用等式的性质解方程:利用等式的性质对方程进行变形,使方程的形式向______________ 的形式转化.
除以
x=a
探究新知
3. 一元一次方程的定义
在一个方程中,只含有______________ ,且方程中的代数式都是整式,未知数的______________都是1,这样的方程叫做一元一次方程.
我们将ax+b=0(其中x是未知数,a,b是已知数,并且a≠0)叫做一元一次方程的标准形式. 这里___________是未知数的系数,__________是常数,___________的指数必须是1.
一个未知数
指数
a
b
x
知识专题
4. 解一元一次方程
解一元一次方程的一般步骤:______________ 、______________ 、_____________ 、______________ 、______________ 化为1.
注意:解方程时,上面的步骤不一定全用到,也不一定完全按上面的步骤顺序进行,要根据方程的特点灵活安排.
去分母
去括号
移项
合并同类项
未知数的系数
知识专题
5. 一元一次方程的应用
利用方程解决实际问题的基本思路如下:首先审题,找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的等量关系,从而列出方程,求解并作答,即设、列、解、答.
知识专题
用一元一次方程解决实际问题的五个步骤:
(1)审:仔细审题,确定______________ 和______________ ,找出它们之间的___________ 关系;
(2)设:设未知数(x),根据实际情况,可__________设未知数(问什么设什么),也可__________设未知数;
(3)列:根据______________ 列出方程;
(4)解:解方程,求出未知数的值;
(5)答:检验未知数的值是否正确,是否符合题意,并完整地写出答句.
已知量
未知量
等量
直接
间接
等量关系
知识专题
A.水箱变高了
1、等体积问题等量关系:
变化前体积(面积)= 变化后体积(面积)
2、周长一定的长方形与正方形中,正方形的面积最大,同等周长的圆的面积最大
知识专题
提醒:
1、首先弄清各种图形的体积、面积、周长公式
2、再弄清变化后两种图形的哪个量是相等的
3、正确的设未知数列方程
知识专题
B.打折销售
1.进价(成本) 2.原价(定价) 3.售价 4.利润 5.利润率 6.折扣
一、此类型中的量
二、此类型中的等量关系
1.标价=成本×(1+提高率)
2.售价=标价×折扣/10
3.利润=售价-进价
知识专题
C.“希望工程”义演
1.引例的等量关系
成人票数+学生票数=总票数
成人票款+学生票款=总票款
2.知识要点
1、方程是ax+b(A-x)=B型的应用题
(a、b、A、B均是已知数)
2、比例分配型应用题
知识专题
D.能追上小明吗?
1.涉及到的量
2.三个基本量之间的关系
(路程 速度 时间)
1)路程=速度×时间
2)速度=路程÷时间
3)时间=路程÷速度
知识专题
3.类似行程问题的工程问题
1)工作总量 = 工作效率 × 工作时间
2)工作效率 = 工作总量 ÷ 工作时间
3)工作时间 = 工作总量 ÷ 工作效率
知识专题
E.教育储蓄
1.涉及量
2.量之间的关系
1.本息和=本金+利息
2.利息税=利息×20%
3.利息=本金×利率×期数
4.利息=本金×利率×期数×(1-20%)
1.本金 2.利息 3.本息和
4.利率(年、月) 5.期数 6.利息税
知识专题
考点专练
1. 下列各式中,是一元一次方程的是( )
A.x+y=x-2 B.x+y=5 C.4x=0 D.6x+5
2. 下列方程的解不是x= 的是( )
A.2x=1 B.-2x+2=3 C.x=1-x D. (x-1)=-
C
B
考点专练
3. 若代数式2x+1和x+5的值相等,x的值为( )
A.2 B.3 C.4 D.5
4. 如果2 005-200.5=x-20.05,那么x等于( )
A.1 814.15 B.1 824.55 C.1 774.45 D.1 784.45
5. 如果关于m的方程2m+b=m-1的解是-4,那么b的值为( )
A.3 B.5 C.-5 D.-13
C
B
A
考点专练
6. 已知方程(m+1)x |m| +3=0是关于x的一元一次方程,则m的值是( )
A.±1 B.1 C.-1 D.0或1
7. 方程 ,去分母,得( )
A.2x-1-x+1=6 B.3(2x-1)-2(x+1)=6
C.2(2x-1)-3(x+1)=6 D.3x-3-2x-2=1
B
B
考点专练
8.如果式子x+2与-2x+4的值是互为相反数,则x的值?
解:根据互为相反的两数之和等于0 可得
x+2+(-2x+4)=0
x+2-2x+4=0
-x+6=0
- x =-6
x =6 所以x的值为6
考点专练
9. 解方程:3(x+1)-(5+x)=18-2(x-1).
解:去括号,得3x+3-5-x=18-2x+2;
移项,得 3x-x+2x=18+2-3+5;
合并同类项,得 4x=22.
系数化为1,得 x= .
考点专练
10. 已知x 2m-3 +6=m是关于x的一元一次方程,试求代数式(m-3) 2 006 的值.
解:由已知x 2m-3 +6=m是关于x的一元一次方程,
得2m-3=1;
解之,得m=2;
从而(m-3) 2 006
=(2-3) 2 006
=(-1) 2 006 =1.
考点专练
11. 小亮家今年承包的鱼塘到期了,共起出鲫鱼和鳊鱼500千克,共卖了2800元,已知鲫鱼和鳊鱼每千克分别为6元和5元,则鲫鱼和鳊鱼各千克.
解:设鲫鱼x千克,则鳊(500-x)千克,
由题意得 6x+5(500-x)=2800
解得x=300
则鳊(500-x)=500-300=200
答:鲫鱼300千克,鳊鱼200千克.
考点专练
12. A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x+80=240
解得 x=2
答:设B车行了2小时后与A车相距80千米。
谢 谢 ~
新课标 北师大版
七年级上册
第五章
一元一次方程
单元小结
中小学教育资源及组卷应用平台
本章知识架构
知识专题
1. 方程的定义
方程的定义:含有______________ 的等式叫做方程.
在这一概念中要抓住方程定义的两个要点:①是______________ ;②含有______________ .
2. 等式的基本性质:
(1)等式的性质
性质1:等式两边同时加(或减)同一个代数式,所得结果仍是______________ ;
未知数
等式
未知数
等式
知识专题
性质2:等式两边同时乘同一个数(或______________ 一个不为零的数),所得结果仍是等式. 此外,等式还具有对称性和传递性,即:
①对称性:如果a=b,那么b=a,即等式的左、右两边交换位置,所得结果仍是等式.
②传递性:如果a=b,且b=c,那么a=c,这一性质也叫做等量代换.
(2)利用等式的性质解方程:利用等式的性质对方程进行变形,使方程的形式向______________ 的形式转化.
除以
x=a
探究新知
3. 一元一次方程的定义
在一个方程中,只含有______________ ,且方程中的代数式都是整式,未知数的______________都是1,这样的方程叫做一元一次方程.
我们将ax+b=0(其中x是未知数,a,b是已知数,并且a≠0)叫做一元一次方程的标准形式. 这里___________是未知数的系数,__________是常数,___________的指数必须是1.
一个未知数
指数
a
b
x
知识专题
4. 解一元一次方程
解一元一次方程的一般步骤:______________ 、______________ 、_____________ 、______________ 、______________ 化为1.
注意:解方程时,上面的步骤不一定全用到,也不一定完全按上面的步骤顺序进行,要根据方程的特点灵活安排.
去分母
去括号
移项
合并同类项
未知数的系数
知识专题
5. 一元一次方程的应用
利用方程解决实际问题的基本思路如下:首先审题,找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的等量关系,从而列出方程,求解并作答,即设、列、解、答.
知识专题
用一元一次方程解决实际问题的五个步骤:
(1)审:仔细审题,确定______________ 和______________ ,找出它们之间的___________ 关系;
(2)设:设未知数(x),根据实际情况,可__________设未知数(问什么设什么),也可__________设未知数;
(3)列:根据______________ 列出方程;
(4)解:解方程,求出未知数的值;
(5)答:检验未知数的值是否正确,是否符合题意,并完整地写出答句.
已知量
未知量
等量
直接
间接
等量关系
知识专题
A.水箱变高了
1、等体积问题等量关系:
变化前体积(面积)= 变化后体积(面积)
2、周长一定的长方形与正方形中,正方形的面积最大,同等周长的圆的面积最大
知识专题
提醒:
1、首先弄清各种图形的体积、面积、周长公式
2、再弄清变化后两种图形的哪个量是相等的
3、正确的设未知数列方程
知识专题
B.打折销售
1.进价(成本) 2.原价(定价) 3.售价 4.利润 5.利润率 6.折扣
一、此类型中的量
二、此类型中的等量关系
1.标价=成本×(1+提高率)
2.售价=标价×折扣/10
3.利润=售价-进价
知识专题
C.“希望工程”义演
1.引例的等量关系
成人票数+学生票数=总票数
成人票款+学生票款=总票款
2.知识要点
1、方程是ax+b(A-x)=B型的应用题
(a、b、A、B均是已知数)
2、比例分配型应用题
知识专题
D.能追上小明吗?
1.涉及到的量
2.三个基本量之间的关系
(路程 速度 时间)
1)路程=速度×时间
2)速度=路程÷时间
3)时间=路程÷速度
知识专题
3.类似行程问题的工程问题
1)工作总量 = 工作效率 × 工作时间
2)工作效率 = 工作总量 ÷ 工作时间
3)工作时间 = 工作总量 ÷ 工作效率
知识专题
E.教育储蓄
1.涉及量
2.量之间的关系
1.本息和=本金+利息
2.利息税=利息×20%
3.利息=本金×利率×期数
4.利息=本金×利率×期数×(1-20%)
1.本金 2.利息 3.本息和
4.利率(年、月) 5.期数 6.利息税
知识专题
考点专练
1. 下列各式中,是一元一次方程的是( )
A.x+y=x-2 B.x+y=5 C.4x=0 D.6x+5
2. 下列方程的解不是x= 的是( )
A.2x=1 B.-2x+2=3 C.x=1-x D. (x-1)=-
C
B
考点专练
3. 若代数式2x+1和x+5的值相等,x的值为( )
A.2 B.3 C.4 D.5
4. 如果2 005-200.5=x-20.05,那么x等于( )
A.1 814.15 B.1 824.55 C.1 774.45 D.1 784.45
5. 如果关于m的方程2m+b=m-1的解是-4,那么b的值为( )
A.3 B.5 C.-5 D.-13
C
B
A
考点专练
6. 已知方程(m+1)x |m| +3=0是关于x的一元一次方程,则m的值是( )
A.±1 B.1 C.-1 D.0或1
7. 方程 ,去分母,得( )
A.2x-1-x+1=6 B.3(2x-1)-2(x+1)=6
C.2(2x-1)-3(x+1)=6 D.3x-3-2x-2=1
B
B
考点专练
8.如果式子x+2与-2x+4的值是互为相反数,则x的值?
解:根据互为相反的两数之和等于0 可得
x+2+(-2x+4)=0
x+2-2x+4=0
-x+6=0
- x =-6
x =6 所以x的值为6
考点专练
9. 解方程:3(x+1)-(5+x)=18-2(x-1).
解:去括号,得3x+3-5-x=18-2x+2;
移项,得 3x-x+2x=18+2-3+5;
合并同类项,得 4x=22.
系数化为1,得 x= .
考点专练
10. 已知x 2m-3 +6=m是关于x的一元一次方程,试求代数式(m-3) 2 006 的值.
解:由已知x 2m-3 +6=m是关于x的一元一次方程,
得2m-3=1;
解之,得m=2;
从而(m-3) 2 006
=(2-3) 2 006
=(-1) 2 006 =1.
考点专练
11. 小亮家今年承包的鱼塘到期了,共起出鲫鱼和鳊鱼500千克,共卖了2800元,已知鲫鱼和鳊鱼每千克分别为6元和5元,则鲫鱼和鳊鱼各千克.
解:设鲫鱼x千克,则鳊(500-x)千克,
由题意得 6x+5(500-x)=2800
解得x=300
则鳊(500-x)=500-300=200
答:鲫鱼300千克,鳊鱼200千克.
考点专练
12. A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x+80=240
解得 x=2
答:设B车行了2小时后与A车相距80千米。
谢 谢 ~
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
