24.5 三角形的内切圆课件(共25张PPT)
文档属性
| 名称 | 24.5 三角形的内切圆课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:12:08 | ||
图片预览





文档简介
(共25张PPT)
三角形的内切圆
24.5 三角形的内切圆
学习目标
1. 了解有关三角形的内切圆和三角形的内心的概念.
2. 掌握三角形内心的性质并能加以应用.
3. 学会利用方程思想解决几何问题,体验数形结合思想.
24.5 三角形的内切圆
有一块三角形材料,如何从中裁下一个面积最大的圆?
情境引入
24.5 三角形的内切圆
讲授新课
若要使裁下的圆形最大,则它与三角形三边应有怎样的位置关系?
最大的圆与三角形三边都相切
24.5 三角形的内切圆
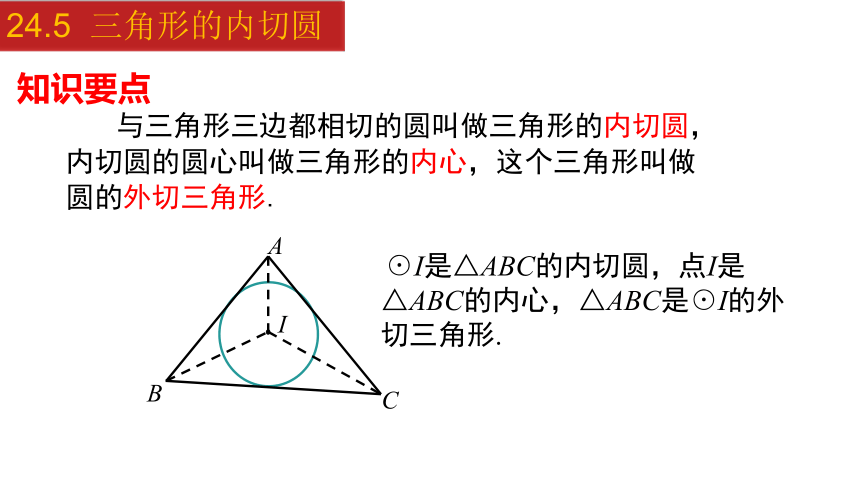
与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
B
A
C
I
知识要点
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
24.5 三角形的内切圆
问题1 如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心O在∠ABC的平分线上.
N
C
O
M
A
B
探究
24.5 三角形的内切圆
C
O
A
B
问题2 如图,如果⊙O与 △ABC的内角∠ABC 的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心O在∠ABC与∠ACB这两个角的平分线的交点上.
线段AO,BO ,CO 分别是∠BAC,∠ABC,∠ACB的平分线.
F
E
D
线段线段OD,OE, OF的长度相等,等于三角形内切圆的半径.
24.5 三角形的内切圆
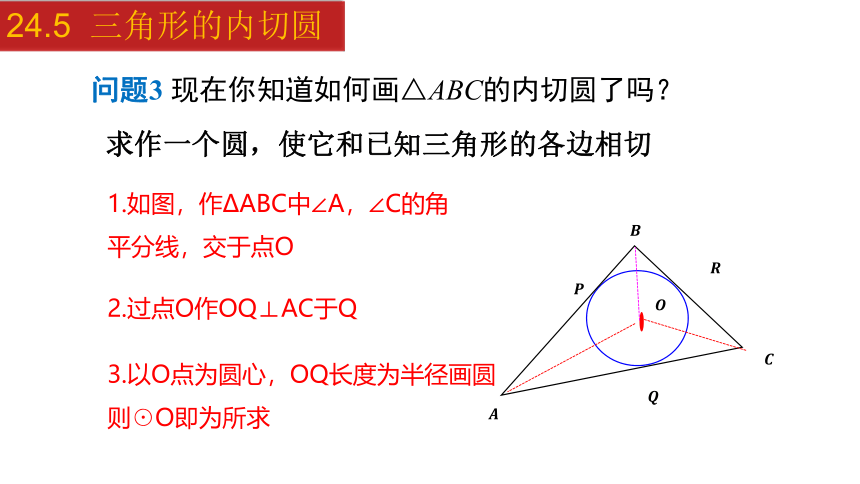
1.如图,作ΔABC中∠A,∠C的角平分线,交于点O
问题3 现在你知道如何画△ABC的内切圆了吗?
2.过点O作OQ⊥AC于Q
3.以O点为圆心,OQ长度为半径画圆
则☉O即为所求
求作一个圆,使它和已知三角形的各边相切
24.5 三角形的内切圆
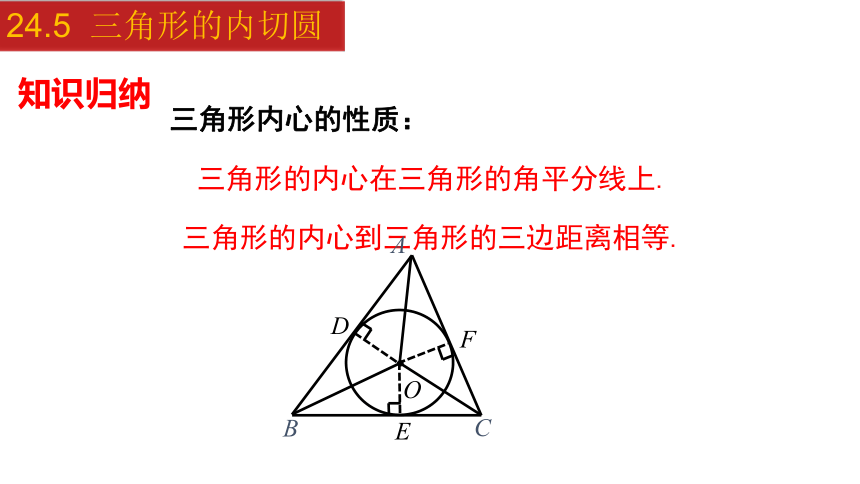
三角形内心的性质:
三角形的内心在三角形的角平分线上.
三角形的内心到三角形的三边距离相等.
C
O
A
B
F
E
D
知识归纳
24.5 三角形的内切圆
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边垂直平分线的交点
1.OA = OB = OC
2.不一定在三角形内部
三角形三条
角平分线的
交点
1.到三边距离相等
2. AO、BO、CO 分别平分∠BAC、∠ABC、∠ACB
3.在三角形内部
A
B
O
C
A
B
C
O
类比归纳
24.5 三角形的内切圆
例1 如图,△ABC中,∠ABC=43°,∠ACB=61 °,点 I 是△ABC的内心,求∠BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点 I 是△ABC的内心,
∴ BI,CI 分别是∠ABC,∠ACB的平分线.
在△IBC中,
24.5 三角形的内切圆
例2 如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱. 圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为 3 cm,求圆柱底面圆的半径.
该问题可以抽象为如下所示的几何图形.
24.5 三角形的内切圆
C
A
B
r
O
D
解: 如图,设圆 O 切 AB 于点 D,连接 OA、OB、OD.
∵ 圆 O 是等边△ABC 的内切圆,
∴ AO、BO 是∠BAC、∠ABC 的平分线.
∴ ∠OAB =∠OBA = 30°.
∵ OD⊥AB,AB = 3 cm,
∴ AD = BD = AB = 1.5 (cm).
∴ OD = AD·tan30° = (cm).
答:圆柱底面圆的半径为 cm.
24.5 三角形的内切圆
例3 △ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D、E、F,且 AB = 13 cm,BC = 14 cm,CA = 9 cm,求 AF、BD、CE 的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
24.5 三角形的内切圆
解:
设 AF = x cm,则 AE = x cm.
∴CE = CD = AC - AE = 9 - x (cm),
BF = BD = AB - AF = 13 - x(cm).
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 cm,BD = 9 cm,CE = 5 cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
解得 x = 4.
B
A
C
E
D
F
O
24.5 三角形的内切圆
例4 如图所示,⊙O是Rt△ABC的内切圆,切点分别为D,E,F,∠C=90°,AC=3,BC=4,求⊙O的半径r.
连接OA,OB,OC,OD,OE,OF,利用S△ABC=S△COB+S△BOA+S△AOC求解.还可以发现四边形OECD 为正方形,则可利用切线长定理,用含r的代数式表示 AB的长,再求解.
分析:
24.5 三角形的内切圆
方法一:如图,连接OA,OB,OC,OD,OE,OF,
则OD=OE=OF=r,OD⊥BC,OE⊥AC,OF⊥AB.
在Rt△ABC中,AB=
∵S△ABC=S△COB+S△BOA+S△AOC,
∴
∴r=
解:
24.5 三角形的内切圆
方法二:如图,连接OD,OE,则OE⊥AC,OD⊥BC,
又∵EC⊥CD,且OE=OD=r,
∴四边形OECD是正方形 .
∴EC=CD=r .
∴AB=AF+BF=AE+BD
=(AC-EC)+(BC-CD)
=3-r+4-r=7-2r .
又易知AB=
∴7-2r=5 ,即r=1 .
24.5 三角形的内切圆
当堂练习
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
1.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
120°
24.5 三角形的内切圆
2. 在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5
C.1,2.5 D.2,2.5
3. 如图,正三角形ABC的内切圆半径为1,那么这个正三角形的边长为( )
A.2 B.3 C. D.2
D
C
24.5 三角形的内切圆
A
B
C
O
c
D
E
r
4.如图,直角三角形的两直角边分别是a、b,斜边为c,则其内切圆的半径r为___________(以含a、b、c的代数式表示r).
解析:如图,过点O分别作AC,BC,AB的垂线,垂足分别为D,E,F.
F
则AD=AC-DC=b-r,
BE=BC-CE=a-r,
因为AF=AD,BF=BE,AF+BF=c,
所以a-r+b-r=c,
所以
b
a
24.5 三角形的内切圆
C
A
B
O
D
5.求边长为6 cm的等边三角形的内切圆半径与外接圆半径.
解:如图,由题意可知BC=6cm,
∠ABC=60°,OD⊥BC,BO平分∠ABC.
∴∠OBD=30°,BD=3cm,
△OBD为直角三角形.
内切圆半径
外接圆半径
24.5 三角形的内切圆
6. △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
24.5 三角形的内切圆
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
有关概念
内心概念及性质
应用
课堂小结
24.5 三角形的内切圆
THANKS
“
”
24.5 三角形的内切圆
三角形的内切圆
24.5 三角形的内切圆
学习目标
1. 了解有关三角形的内切圆和三角形的内心的概念.
2. 掌握三角形内心的性质并能加以应用.
3. 学会利用方程思想解决几何问题,体验数形结合思想.
24.5 三角形的内切圆
有一块三角形材料,如何从中裁下一个面积最大的圆?
情境引入
24.5 三角形的内切圆
讲授新课
若要使裁下的圆形最大,则它与三角形三边应有怎样的位置关系?
最大的圆与三角形三边都相切
24.5 三角形的内切圆
与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
B
A
C
I
知识要点
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
24.5 三角形的内切圆
问题1 如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心O在∠ABC的平分线上.
N
C
O
M
A
B
探究
24.5 三角形的内切圆
C
O
A
B
问题2 如图,如果⊙O与 △ABC的内角∠ABC 的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心O在∠ABC与∠ACB这两个角的平分线的交点上.
线段AO,BO ,CO 分别是∠BAC,∠ABC,∠ACB的平分线.
F
E
D
线段线段OD,OE, OF的长度相等,等于三角形内切圆的半径.
24.5 三角形的内切圆
1.如图,作ΔABC中∠A,∠C的角平分线,交于点O
问题3 现在你知道如何画△ABC的内切圆了吗?
2.过点O作OQ⊥AC于Q
3.以O点为圆心,OQ长度为半径画圆
则☉O即为所求
求作一个圆,使它和已知三角形的各边相切
24.5 三角形的内切圆
三角形内心的性质:
三角形的内心在三角形的角平分线上.
三角形的内心到三角形的三边距离相等.
C
O
A
B
F
E
D
知识归纳
24.5 三角形的内切圆
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边垂直平分线的交点
1.OA = OB = OC
2.不一定在三角形内部
三角形三条
角平分线的
交点
1.到三边距离相等
2. AO、BO、CO 分别平分∠BAC、∠ABC、∠ACB
3.在三角形内部
A
B
O
C
A
B
C
O
类比归纳
24.5 三角形的内切圆
例1 如图,△ABC中,∠ABC=43°,∠ACB=61 °,点 I 是△ABC的内心,求∠BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点 I 是△ABC的内心,
∴ BI,CI 分别是∠ABC,∠ACB的平分线.
在△IBC中,
24.5 三角形的内切圆
例2 如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱. 圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为 3 cm,求圆柱底面圆的半径.
该问题可以抽象为如下所示的几何图形.
24.5 三角形的内切圆
C
A
B
r
O
D
解: 如图,设圆 O 切 AB 于点 D,连接 OA、OB、OD.
∵ 圆 O 是等边△ABC 的内切圆,
∴ AO、BO 是∠BAC、∠ABC 的平分线.
∴ ∠OAB =∠OBA = 30°.
∵ OD⊥AB,AB = 3 cm,
∴ AD = BD = AB = 1.5 (cm).
∴ OD = AD·tan30° = (cm).
答:圆柱底面圆的半径为 cm.
24.5 三角形的内切圆
例3 △ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D、E、F,且 AB = 13 cm,BC = 14 cm,CA = 9 cm,求 AF、BD、CE 的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
24.5 三角形的内切圆
解:
设 AF = x cm,则 AE = x cm.
∴CE = CD = AC - AE = 9 - x (cm),
BF = BD = AB - AF = 13 - x(cm).
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 cm,BD = 9 cm,CE = 5 cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
解得 x = 4.
B
A
C
E
D
F
O
24.5 三角形的内切圆
例4 如图所示,⊙O是Rt△ABC的内切圆,切点分别为D,E,F,∠C=90°,AC=3,BC=4,求⊙O的半径r.
连接OA,OB,OC,OD,OE,OF,利用S△ABC=S△COB+S△BOA+S△AOC求解.还可以发现四边形OECD 为正方形,则可利用切线长定理,用含r的代数式表示 AB的长,再求解.
分析:
24.5 三角形的内切圆
方法一:如图,连接OA,OB,OC,OD,OE,OF,
则OD=OE=OF=r,OD⊥BC,OE⊥AC,OF⊥AB.
在Rt△ABC中,AB=
∵S△ABC=S△COB+S△BOA+S△AOC,
∴
∴r=
解:
24.5 三角形的内切圆
方法二:如图,连接OD,OE,则OE⊥AC,OD⊥BC,
又∵EC⊥CD,且OE=OD=r,
∴四边形OECD是正方形 .
∴EC=CD=r .
∴AB=AF+BF=AE+BD
=(AC-EC)+(BC-CD)
=3-r+4-r=7-2r .
又易知AB=
∴7-2r=5 ,即r=1 .
24.5 三角形的内切圆
当堂练习
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
1.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
120°
24.5 三角形的内切圆
2. 在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5
C.1,2.5 D.2,2.5
3. 如图,正三角形ABC的内切圆半径为1,那么这个正三角形的边长为( )
A.2 B.3 C. D.2
D
C
24.5 三角形的内切圆
A
B
C
O
c
D
E
r
4.如图,直角三角形的两直角边分别是a、b,斜边为c,则其内切圆的半径r为___________(以含a、b、c的代数式表示r).
解析:如图,过点O分别作AC,BC,AB的垂线,垂足分别为D,E,F.
F
则AD=AC-DC=b-r,
BE=BC-CE=a-r,
因为AF=AD,BF=BE,AF+BF=c,
所以a-r+b-r=c,
所以
b
a
24.5 三角形的内切圆
C
A
B
O
D
5.求边长为6 cm的等边三角形的内切圆半径与外接圆半径.
解:如图,由题意可知BC=6cm,
∠ABC=60°,OD⊥BC,BO平分∠ABC.
∴∠OBD=30°,BD=3cm,
△OBD为直角三角形.
内切圆半径
外接圆半径
24.5 三角形的内切圆
6. △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
24.5 三角形的内切圆
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
有关概念
内心概念及性质
应用
课堂小结
24.5 三角形的内切圆
THANKS
“
”
24.5 三角形的内切圆
