15.2.3 整数指数幂 (第1课时) 整数指数幂 课件 (共17张PPT)
文档属性
| 名称 | 15.2.3 整数指数幂 (第1课时) 整数指数幂 课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:41:46 | ||
图片预览





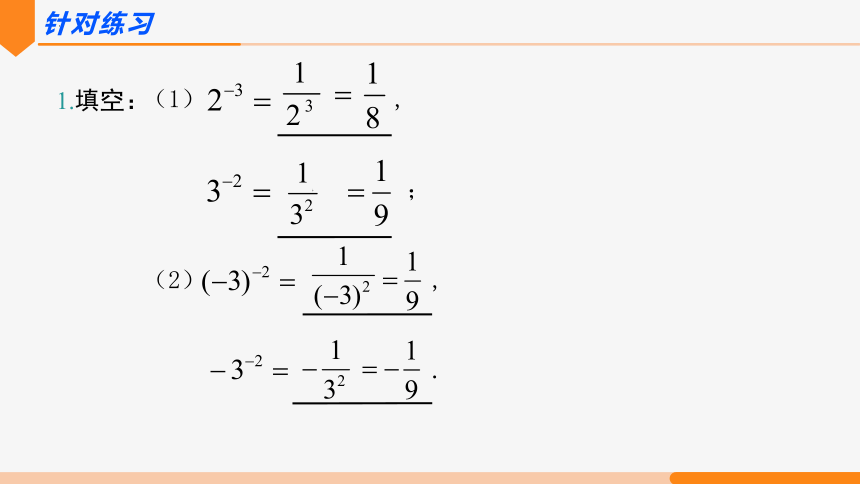

文档简介
(共17张PPT)
整数指数幂
15.2.3 整数指数幂
| 第1课时|
回顾知识
练习:计算下列各题,回顾相关的幂的运算。
(1) a×a×a…×a=
n个a
(2) x2 · x5 =
(3) (x2) 5 =
(4) (x2y) 5 =
(5) x6 ÷ x3 =
(6) x6 ÷ x6 =
1.同底数幂的乘法:
2.幂的乘方:
3.积的乘方:
4.同底数幂的除法:
6.商的乘方:
5.零次方:
幂的运算
am ÷ an = am-n
am · an = am+n
(am )n = amn
(ab)n = anbn
a0 = 1
(a≠0).
(a≠0).
(a≠0).
探究新知
思考:
问题2 计算:a3 ÷a5= (a ≠0),你得出什么结论?
解法1
解法2 a3÷a5=a3-5=a-2.
于是得到:
归纳知识
负整数指数幂的意义
这就是说,a-n (a≠0)是 an 的倒数.
(1) ,
;
(2) ,
.
针对练习
1.填空:
思考:
问题3 引入负整数指数幂后,指数的取值范围就推广到全体整数.前面提到的运算性质还成吗?请举例说明.
归纳知识
负整数指数幂的意义
这就是说,a-n (a≠0)是 an 的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数.也就说前面提到的运算性质也推广到整数指数幂.
典例讲解
例1 计算:
(1)
(2)
(3)
(4)
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
计算:
(1)(3x2y-2)2÷(x-2y)3; (2)(3×10-5)3÷(3×10-6)2.
(3)
例2
(2)原式=(27×10-15)÷(9×10-12)
=3×10-3
解:(1)原式=9x4y-4÷x-6y3
=9x10y-7
(3)=1-8-3+2
=-8.
针对练习
1.计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
2.计算
解:原式
归纳知识
整数指数幂的运算性质
(1)am·an=am+n ( m、n是整数,a≠0) ;
(2)(am)n=amn ( m、n是整数,a≠0) ;
(3)(ab)n=anbn ( n是整数,a≠0,b≠0).
课堂小结
整数指数幂运算
零指数幂
a0=1 (a≠0)
负整数指数幂
整数指数幂
am·an=am+n ( m、n是整数,a≠0) ;
(am)n=amn ( m、n是整数,a≠0)
(ab)n=anbn ( n是整数,a≠0,b≠0).
课堂练习
1. 2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
A
2. (-2)-2等于( )
A.-4 B.4 C. D.
D
3 计算a·a-1的结果为( )
A.-1 B.0 C.1 D.-a
C
4.下列运算正确的是( )
A. B.6 ×107=6000000
C. (2a)2 =2a2 D.a3 ·a2=a5
D
5.若(x-3)0-2(3x-6)-2有意义,则x的取值范围是( )
A.x>3 B.x≠3且x≠2
C.x≠3或x≠2 D.x<2
B
6.计算:
(1)0.1÷0.13; (2)(-5)2018÷(-5)2020;
(3)100×10-1÷10-2; (4)x-2·x-3÷x2.
解.(1)原式=
(2)原式=
(3)原式=
(4)原式=
(1)(2×10-6)× (3.2×103);
(2)(2×10-6)2 ÷ (10-4)3.
= 6.4×10-3;
= 4.
7.计算:
整数指数幂
15.2.3 整数指数幂
| 第1课时|
回顾知识
练习:计算下列各题,回顾相关的幂的运算。
(1) a×a×a…×a=
n个a
(2) x2 · x5 =
(3) (x2) 5 =
(4) (x2y) 5 =
(5) x6 ÷ x3 =
(6) x6 ÷ x6 =
1.同底数幂的乘法:
2.幂的乘方:
3.积的乘方:
4.同底数幂的除法:
6.商的乘方:
5.零次方:
幂的运算
am ÷ an = am-n
am · an = am+n
(am )n = amn
(ab)n = anbn
a0 = 1
(a≠0).
(a≠0).
(a≠0).
探究新知
思考:
问题2 计算:a3 ÷a5= (a ≠0),你得出什么结论?
解法1
解法2 a3÷a5=a3-5=a-2.
于是得到:
归纳知识
负整数指数幂的意义
这就是说,a-n (a≠0)是 an 的倒数.
(1) ,
;
(2) ,
.
针对练习
1.填空:
思考:
问题3 引入负整数指数幂后,指数的取值范围就推广到全体整数.前面提到的运算性质还成吗?请举例说明.
归纳知识
负整数指数幂的意义
这就是说,a-n (a≠0)是 an 的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数.也就说前面提到的运算性质也推广到整数指数幂.
典例讲解
例1 计算:
(1)
(2)
(3)
(4)
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
计算:
(1)(3x2y-2)2÷(x-2y)3; (2)(3×10-5)3÷(3×10-6)2.
(3)
例2
(2)原式=(27×10-15)÷(9×10-12)
=3×10-3
解:(1)原式=9x4y-4÷x-6y3
=9x10y-7
(3)=1-8-3+2
=-8.
针对练习
1.计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
2.计算
解:原式
归纳知识
整数指数幂的运算性质
(1)am·an=am+n ( m、n是整数,a≠0) ;
(2)(am)n=amn ( m、n是整数,a≠0) ;
(3)(ab)n=anbn ( n是整数,a≠0,b≠0).
课堂小结
整数指数幂运算
零指数幂
a0=1 (a≠0)
负整数指数幂
整数指数幂
am·an=am+n ( m、n是整数,a≠0) ;
(am)n=amn ( m、n是整数,a≠0)
(ab)n=anbn ( n是整数,a≠0,b≠0).
课堂练习
1. 2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
A
2. (-2)-2等于( )
A.-4 B.4 C. D.
D
3 计算a·a-1的结果为( )
A.-1 B.0 C.1 D.-a
C
4.下列运算正确的是( )
A. B.6 ×107=6000000
C. (2a)2 =2a2 D.a3 ·a2=a5
D
5.若(x-3)0-2(3x-6)-2有意义,则x的取值范围是( )
A.x>3 B.x≠3且x≠2
C.x≠3或x≠2 D.x<2
B
6.计算:
(1)0.1÷0.13; (2)(-5)2018÷(-5)2020;
(3)100×10-1÷10-2; (4)x-2·x-3÷x2.
解.(1)原式=
(2)原式=
(3)原式=
(4)原式=
(1)(2×10-6)× (3.2×103);
(2)(2×10-6)2 ÷ (10-4)3.
= 6.4×10-3;
= 4.
7.计算:
