6.4 数据的离散程度 课件 (共46张PPT)
文档属性
| 名称 | 6.4 数据的离散程度 课件 (共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:37:31 | ||
图片预览











文档简介
(共46张PPT)
第4课时数据的离散程度
思考1 分别计算两名射击选手的平均成绩.
甲选手的平均成绩为: = 8环.
乙选手的平均成绩为: = 8环.
知识点:方差
新知探究
思考2 请根据这两名射击选手的成绩在图中画出折线统计图.
0
1
2
3
4
5
成绩/环
射击顺序
2
4
6
8
10
乙
甲
思考3 假如你是教练,你认为选择哪一位射击选手更合适?
甲、乙两名选手的平均成绩一样,但从图表来看,甲的成绩上下浮动性小,相对稳定,所以选择甲更合适.
例1 农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题,为了解甲、乙两种甜玉米种子的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如表所示.
甲 7.65 7.50 7.62 7.59 7.65 7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49 7.52 7.58 7.46 7.53 7.49
甲、乙两种甜玉米的平均产量相差不大,由此可以估计出这个地区种植这两种甜玉米,它们的平均产量相差不大.
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
上面两组数据的平均数分别是甲=7.537,=7.515.
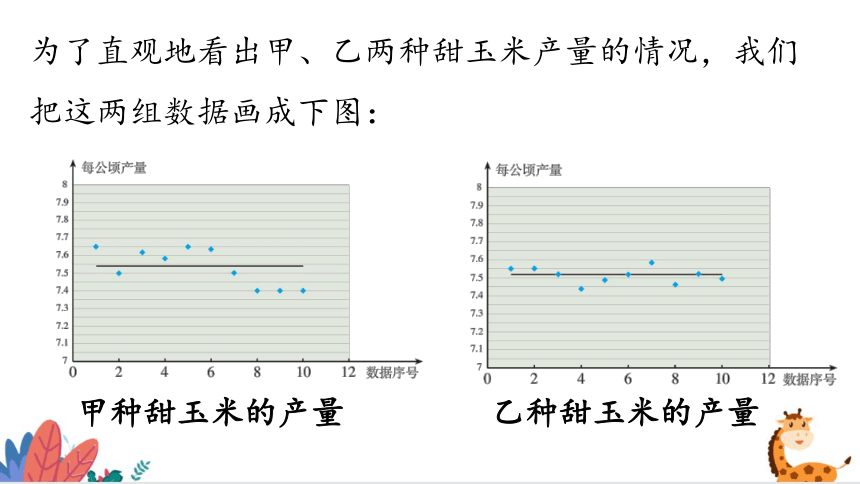
为了直观地看出甲、乙两种甜玉米产量的情况,我们把这两组数据画成下图:
甲种甜玉米的产量
乙种甜玉米的产量
比较上面两幅图可以看出,甲种甜玉米在各试验田的产量波动较大,乙种甜玉米在各试验田的产量比较集中地分布在平均产量附近.
从图中看出的结果能否用一个量来刻画呢?
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是
,,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
方差可以反映数据的波动程度:方差越大,数据的波动越大;方差越小,数据的波动越小.
甲、乙两组数据的方差分别是:
≈0.010.
≈0.002.
∵∴乙种甜玉米的产量比较稳定.
综合考虑甲、乙两个品种的平均产量和产量的稳定性,可以推测这个地区适合种植乙种甜玉米.
求方差的一般步骤:(1)求原始数据的平均数;
(2)求原始数据中各数据与平均数的差;
(3)将所得的差分别平方;
(4)求(3)中所得数据的平均数.
拓展:方差的简化计算公式为:
.
例2 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如表所示.
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的身高平均数分别是
=166.
=165.
1.5.
.
由可知,甲芭蕾舞团女演员的身高更整齐.
方差分别是
用计算器求方差
使用计算器的统计功能求方差时,通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1, x2, , xn最后按动求方差的功能键,计算器便会求出方差的值.
如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
丙厂这20只鸡腿质量的平均数为75.1克,极差是7克。
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?
可分别用这20只鸡腿的质量与其平均数差的绝对值刻画。
(3)分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
甲厂的差距依
次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
(4)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
差距和
较小
甲厂的差距依
次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
差距和
较大
数学上,数据的离散程度还可以用方差和标准差刻画。
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
1.方差和标准差
例3 (1)分别计算出从甲、丙两厂抽取的20只鸡腿质量的方差?
(2)根据计算的结果,你认为哪家的产品更符合规格?
丙厂:
4.2
(2)甲厂更符合规定.
解:甲厂:
2.5
实际生活中,除了关心数据的“平均水平”外,人们往往还关注数据的离散程度,即它们相对于“平均水平”的偏离情况.极差就是刻画数据的离散程度的一个统计量.
极差是指一组数据中最大数据与最小数据的差.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
2.极差
从这个问题中我们发现:
1. 平均数对于数据分析只能反映它们的平均值,在实际
问题的研究中,还有很大的局限性.
如上面这个问题中,平均数都是75,事实上甲厂的产品更符合要求.
2. 讨论数据的离散程度可以用“极差”这个统计量来
刻画.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
结论
例1 A县的“味加味”快餐店销售的奥尔良鸡腿非常受大众的欢迎,需要大量的鸡腿供货.现有甲、乙两个供货商到“味加味”推销自己的鸡腿,目前来看两家的鸡腿价格相同,品质也相近,快餐店经理决定通过检查鸡腿的质量来确定哪家鸡腿能够满足他们的需求.
知识点:用样本方差估计总体方差
新知探究
(1)快餐店可以通过哪些数据来体现鸡腿的质量?
每个鸡腿的质量;鸡腿质量的稳定性.
(2)鸡腿的数量较多,无法进行一一的测量比较,你能帮助快餐店经理想出解决办法吗?
采取抽样调查,利用样本来估计总体.
甲 79 72 73 72 75 73 71 76 78 78 77 74 75 80 71
乙 72 77 74 74 73 75 73 76 76 78 74 74 75 76 73
(3)快餐店员工从甲、乙两家鸡腿中各随机抽取15 个,将它们的质量记录在下表,请你根据表中的数据确定选择哪家供货商?
利用什么数值确定呢?
解:甲供货商 15 个样品的平均数是 ≈ 75.
乙供货商 15 个样品的平均数是 ≈ 75.
从甲、乙供货商提供样本的平均数来看,鸡腿的质量相近,无法判断出各家的好坏.
甲 79 72 73 72 75 73 71 76 78 78 77 74 75 80 71
乙 72 77 74 74 73 75 73 76 76 78 74 74 75 76 73
甲供货商15个样品的方差是 ≈ 8.
从甲、乙供货商提供样本的方差来看,乙供货商提供的鸡腿质量更稳定,所以应该选择乙.
乙供货商15个样品的方差是 ≈ 3.
归纳:用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
例2 某跳远队准备从小明、小刚两人中选取成绩稳定的一个参加市级比赛,已知小明 10 次的测验成绩为 5.85,5.93,6.07,5.91,5.99,6.13,5.98,6.05,6.00,6.19;小刚 10 次测验的成绩为 6.11,6.08,5.83,5.92,5.84,5.81,6.18,6.17,5.85,6.21. 试通过计算判断应该选择谁参加比赛.
如何确定呢?
解:小明 10 次成绩的平均数是
= 6.01.
小刚 10 次成绩的平均数是
= 6.00.
从小明、小刚 10 次成绩的平均数来看,小明的平均成绩更好一些.
小明 10 次成绩的方差是=0.00954.
通过比较方差,小明的成绩更稳定,所以综合考虑应该选择小明参加市级比赛.
小刚 10 次成绩的方差是=0.02434.
1.(2021 包头中考)某人5次射击命中的环数分别为5,10,7,x,10.若这组数据的中位数为8,则这组数据的方差为 _____.
3.6
解析:根据题意,数据5,10,7,x,10的中位数为8,
则x=8,这组数据的平均数为 × (5+10+7+8+10)=8,
则这组数据的方差S2=
×[(5﹣8)2+(10﹣8)2+(7﹣8)2+(8﹣8)2+(10﹣8)2]=3.6 .
随堂练习
2.两台机器同时装质量为 10kg 的桶装花生油,为了检验每一桶中的质量是否达到 10kg,质量检验员从两台机器所装的油桶中各抽取 4 桶进行检测,测量数据(单位:kg)如下:
甲机器 10 9.8 10 10.2
乙机器 10.1 10 9.9 10
如果你是检验员,取得以上数据后,你将通过怎样的运算来判断哪台机器所装的油的质量更符合要求?
解:由题意可知 =10(kg),
=10(kg),
=0.02 ,
.
∵,
∴乙机器所装的油的质量更符合要求.
3.一组数据 4,5,6,x 的众数与中位数相等,则这组数据的方差是 .
由此得到什么?
易错警示:因为题设中x的值不确定,且已知的三个数据都不相同,所以众数是其中的某一个数据,故需分三种情况进行讨论求解.
解析:依据题意,众数可能是4,5,6,所以需要分三种情况进行讨论:
(1)众数是4的时候,则数据为4,4,5,6,此时中位数为4.5,不符合题意.
(2)众数是5的时候,则数据为4,5,5,6,此时中位数为5,符合题意.
此时平均数为=5,方差为
(3)众数是6的时候,则数据为4,5,6,6,此时中位数为5.5,不符合题意.
故这组数据的方差为.
1.某市体委决定从甲、乙两名射击运动员中选拔一名参加大学生冬季运动会,每人各打靶5次,打中环数如下:
甲:7,8,9,8,8 乙:5,10,6,9,10
请根据以上数据分析应该选派哪位运动员参加运动会.
拓展提升
分析:先分别计算出甲、乙二人打靶成绩的平均数和方差,然后依据体育比赛的特性比较二者成绩的优劣,最终做出决定.
解:通过计算可得= 8环,= 8环,
= 0.4, =4.4.
从平均数来看,成绩相同;从方差来看,甲的成绩更稳定一些.但是竞技比赛中,还要比较二人的高分情况,从数据可以看出乙的最高成绩为10环,并且有两次,所以应该选择乙参加运动会.
2.新建成的实验小学准备购置一批新的课桌椅,现有两个家具店的课桌椅的质量、价钱均相同.按照规定,中小学的课桌高度应在 70cm 左右,椅子的高度应在 40cm 左右.学校分别从这两个家具店随机选择了 5 套桌椅,测得的高度(单位:cm)如下表所示,请你通过适当的计算帮助学校选择合适的课桌椅.
1号家具店课桌 72 69 71 70 69
1号家具店椅子 39 40 40 41 41
2号家具店课桌 68 71 72 70 69
2号家具店椅子 42 41 39 40 39
解:1号家具店课桌的平均高度为:=70.2.
1号家具店椅子的平均高度为:=40.2.
2号家具店课桌的平均高度为:=70.
2号家具店椅子的平均高度为:=40.2.
从平均数来看,1号和2号家具店的桌椅均能达到标准.
1号家具店课桌的方差
=1.36.
1号家具店椅子的方差
=0.56.
2号家具店课桌的方差=2.
2号家具店椅子的方差=1.36.
∵1号和2号家具店的桌椅均能达到标准,但是1号家具店的桌椅的方差均小于2号家具店的桌椅的方差,
∴1号家具店的桌椅高度更加整齐一些,学校应该选择1号家具店.
第4课时数据的离散程度
思考1 分别计算两名射击选手的平均成绩.
甲选手的平均成绩为: = 8环.
乙选手的平均成绩为: = 8环.
知识点:方差
新知探究
思考2 请根据这两名射击选手的成绩在图中画出折线统计图.
0
1
2
3
4
5
成绩/环
射击顺序
2
4
6
8
10
乙
甲
思考3 假如你是教练,你认为选择哪一位射击选手更合适?
甲、乙两名选手的平均成绩一样,但从图表来看,甲的成绩上下浮动性小,相对稳定,所以选择甲更合适.
例1 农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题,为了解甲、乙两种甜玉米种子的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如表所示.
甲 7.65 7.50 7.62 7.59 7.65 7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49 7.52 7.58 7.46 7.53 7.49
甲、乙两种甜玉米的平均产量相差不大,由此可以估计出这个地区种植这两种甜玉米,它们的平均产量相差不大.
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
上面两组数据的平均数分别是甲=7.537,=7.515.
为了直观地看出甲、乙两种甜玉米产量的情况,我们把这两组数据画成下图:
甲种甜玉米的产量
乙种甜玉米的产量
比较上面两幅图可以看出,甲种甜玉米在各试验田的产量波动较大,乙种甜玉米在各试验田的产量比较集中地分布在平均产量附近.
从图中看出的结果能否用一个量来刻画呢?
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是
,,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
方差可以反映数据的波动程度:方差越大,数据的波动越大;方差越小,数据的波动越小.
甲、乙两组数据的方差分别是:
≈0.010.
≈0.002.
∵∴乙种甜玉米的产量比较稳定.
综合考虑甲、乙两个品种的平均产量和产量的稳定性,可以推测这个地区适合种植乙种甜玉米.
求方差的一般步骤:(1)求原始数据的平均数;
(2)求原始数据中各数据与平均数的差;
(3)将所得的差分别平方;
(4)求(3)中所得数据的平均数.
拓展:方差的简化计算公式为:
.
例2 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如表所示.
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的身高平均数分别是
=166.
=165.
1.5.
.
由可知,甲芭蕾舞团女演员的身高更整齐.
方差分别是
用计算器求方差
使用计算器的统计功能求方差时,通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1, x2, , xn最后按动求方差的功能键,计算器便会求出方差的值.
如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
丙厂这20只鸡腿质量的平均数为75.1克,极差是7克。
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?
可分别用这20只鸡腿的质量与其平均数差的绝对值刻画。
(3)分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
甲厂的差距依
次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
(4)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
差距和
较小
甲厂的差距依
次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
差距和
较大
数学上,数据的离散程度还可以用方差和标准差刻画。
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
1.方差和标准差
例3 (1)分别计算出从甲、丙两厂抽取的20只鸡腿质量的方差?
(2)根据计算的结果,你认为哪家的产品更符合规格?
丙厂:
4.2
(2)甲厂更符合规定.
解:甲厂:
2.5
实际生活中,除了关心数据的“平均水平”外,人们往往还关注数据的离散程度,即它们相对于“平均水平”的偏离情况.极差就是刻画数据的离散程度的一个统计量.
极差是指一组数据中最大数据与最小数据的差.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
2.极差
从这个问题中我们发现:
1. 平均数对于数据分析只能反映它们的平均值,在实际
问题的研究中,还有很大的局限性.
如上面这个问题中,平均数都是75,事实上甲厂的产品更符合要求.
2. 讨论数据的离散程度可以用“极差”这个统计量来
刻画.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
结论
例1 A县的“味加味”快餐店销售的奥尔良鸡腿非常受大众的欢迎,需要大量的鸡腿供货.现有甲、乙两个供货商到“味加味”推销自己的鸡腿,目前来看两家的鸡腿价格相同,品质也相近,快餐店经理决定通过检查鸡腿的质量来确定哪家鸡腿能够满足他们的需求.
知识点:用样本方差估计总体方差
新知探究
(1)快餐店可以通过哪些数据来体现鸡腿的质量?
每个鸡腿的质量;鸡腿质量的稳定性.
(2)鸡腿的数量较多,无法进行一一的测量比较,你能帮助快餐店经理想出解决办法吗?
采取抽样调查,利用样本来估计总体.
甲 79 72 73 72 75 73 71 76 78 78 77 74 75 80 71
乙 72 77 74 74 73 75 73 76 76 78 74 74 75 76 73
(3)快餐店员工从甲、乙两家鸡腿中各随机抽取15 个,将它们的质量记录在下表,请你根据表中的数据确定选择哪家供货商?
利用什么数值确定呢?
解:甲供货商 15 个样品的平均数是 ≈ 75.
乙供货商 15 个样品的平均数是 ≈ 75.
从甲、乙供货商提供样本的平均数来看,鸡腿的质量相近,无法判断出各家的好坏.
甲 79 72 73 72 75 73 71 76 78 78 77 74 75 80 71
乙 72 77 74 74 73 75 73 76 76 78 74 74 75 76 73
甲供货商15个样品的方差是 ≈ 8.
从甲、乙供货商提供样本的方差来看,乙供货商提供的鸡腿质量更稳定,所以应该选择乙.
乙供货商15个样品的方差是 ≈ 3.
归纳:用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
例2 某跳远队准备从小明、小刚两人中选取成绩稳定的一个参加市级比赛,已知小明 10 次的测验成绩为 5.85,5.93,6.07,5.91,5.99,6.13,5.98,6.05,6.00,6.19;小刚 10 次测验的成绩为 6.11,6.08,5.83,5.92,5.84,5.81,6.18,6.17,5.85,6.21. 试通过计算判断应该选择谁参加比赛.
如何确定呢?
解:小明 10 次成绩的平均数是
= 6.01.
小刚 10 次成绩的平均数是
= 6.00.
从小明、小刚 10 次成绩的平均数来看,小明的平均成绩更好一些.
小明 10 次成绩的方差是=0.00954.
通过比较方差,小明的成绩更稳定,所以综合考虑应该选择小明参加市级比赛.
小刚 10 次成绩的方差是=0.02434.
1.(2021 包头中考)某人5次射击命中的环数分别为5,10,7,x,10.若这组数据的中位数为8,则这组数据的方差为 _____.
3.6
解析:根据题意,数据5,10,7,x,10的中位数为8,
则x=8,这组数据的平均数为 × (5+10+7+8+10)=8,
则这组数据的方差S2=
×[(5﹣8)2+(10﹣8)2+(7﹣8)2+(8﹣8)2+(10﹣8)2]=3.6 .
随堂练习
2.两台机器同时装质量为 10kg 的桶装花生油,为了检验每一桶中的质量是否达到 10kg,质量检验员从两台机器所装的油桶中各抽取 4 桶进行检测,测量数据(单位:kg)如下:
甲机器 10 9.8 10 10.2
乙机器 10.1 10 9.9 10
如果你是检验员,取得以上数据后,你将通过怎样的运算来判断哪台机器所装的油的质量更符合要求?
解:由题意可知 =10(kg),
=10(kg),
=0.02 ,
.
∵,
∴乙机器所装的油的质量更符合要求.
3.一组数据 4,5,6,x 的众数与中位数相等,则这组数据的方差是 .
由此得到什么?
易错警示:因为题设中x的值不确定,且已知的三个数据都不相同,所以众数是其中的某一个数据,故需分三种情况进行讨论求解.
解析:依据题意,众数可能是4,5,6,所以需要分三种情况进行讨论:
(1)众数是4的时候,则数据为4,4,5,6,此时中位数为4.5,不符合题意.
(2)众数是5的时候,则数据为4,5,5,6,此时中位数为5,符合题意.
此时平均数为=5,方差为
(3)众数是6的时候,则数据为4,5,6,6,此时中位数为5.5,不符合题意.
故这组数据的方差为.
1.某市体委决定从甲、乙两名射击运动员中选拔一名参加大学生冬季运动会,每人各打靶5次,打中环数如下:
甲:7,8,9,8,8 乙:5,10,6,9,10
请根据以上数据分析应该选派哪位运动员参加运动会.
拓展提升
分析:先分别计算出甲、乙二人打靶成绩的平均数和方差,然后依据体育比赛的特性比较二者成绩的优劣,最终做出决定.
解:通过计算可得= 8环,= 8环,
= 0.4, =4.4.
从平均数来看,成绩相同;从方差来看,甲的成绩更稳定一些.但是竞技比赛中,还要比较二人的高分情况,从数据可以看出乙的最高成绩为10环,并且有两次,所以应该选择乙参加运动会.
2.新建成的实验小学准备购置一批新的课桌椅,现有两个家具店的课桌椅的质量、价钱均相同.按照规定,中小学的课桌高度应在 70cm 左右,椅子的高度应在 40cm 左右.学校分别从这两个家具店随机选择了 5 套桌椅,测得的高度(单位:cm)如下表所示,请你通过适当的计算帮助学校选择合适的课桌椅.
1号家具店课桌 72 69 71 70 69
1号家具店椅子 39 40 40 41 41
2号家具店课桌 68 71 72 70 69
2号家具店椅子 42 41 39 40 39
解:1号家具店课桌的平均高度为:=70.2.
1号家具店椅子的平均高度为:=40.2.
2号家具店课桌的平均高度为:=70.
2号家具店椅子的平均高度为:=40.2.
从平均数来看,1号和2号家具店的桌椅均能达到标准.
1号家具店课桌的方差
=1.36.
1号家具店椅子的方差
=0.56.
2号家具店课桌的方差=2.
2号家具店椅子的方差=1.36.
∵1号和2号家具店的桌椅均能达到标准,但是1号家具店的桌椅的方差均小于2号家具店的桌椅的方差,
∴1号家具店的桌椅高度更加整齐一些,学校应该选择1号家具店.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
