人教版新教材必修二 5.2 运动的合成与分解绳连速度专题(含答案)
文档属性
| 名称 | 人教版新教材必修二 5.2 运动的合成与分解绳连速度专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 500.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-26 12:49:39 | ||
图片预览

文档简介
人教版新教材必修二第五章绳连速度专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,人在岸上拉船,已知船的质量为,水的阻力恒为,当轻绳与水平面的夹角为时,船的速度为,此时人的拉力大小为,则( )
A. 船的加速度为 B. 船的加速度为
C. 人拉绳行走的速度为 D. 人拉绳行走的速度为
如图所示,物体以速度沿杆匀速下滑,用细绳通过定滑轮拉物体,当绳与水平夹角为时,的速度为( )
A. B. C. D.
如下图所示,有一竖直放置的“”形架,表面光滑,滑块、分别套在水平杆与竖直杆上,、用一不可伸长的轻细绳相连,、质量相等,且可看作质点,开始时细绳水平伸直,、静止.由静止释放后,已知当细绳与竖直方向的夹角为时,滑块沿着竖直杆下滑的速度大小为,则此时的速度大小为( )
A. B. C. D.
固定在竖直平面内的半圆形刚性铁环,半径为,铁环上穿着小球,铁环圆心的正上方固定一个小定滑轮。用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从点开始沿铁环运动,某时刻角度关系如下图所示,若绳末端速度为则小球此时的速度为( )
A. B. C. D.
一个长直轻杆两端分别固定一个小球和,两小球质量均为,大小忽略不计,杆的长度为。先将杆竖直靠放在竖直墙上,如图所示,轻轻振动小球,使小球在水平面上由静止开始向右滑动,当小球沿墙下滑距离为时,下列说法正确的是不计一切摩擦( )
A. 小球和的速度都为 B. 小球和的速度都为
C. 小球、的速度分别为和 D. 小球、的速度分别为和
如图所示,轻绳跨过两个光滑定滑轮连接物块和,其中物块套在水平杆上。图示位置,细线与水平杆的夹角,的速度方向向右,大小为。则物块的速度大小为
A. B. C. D.
质量为的物体置于倾角为的固定光滑斜面上,斜面足够长,轻细绳跨过光滑定滑轮分别连接着与动力小车,与滑轮间的细绳平行于斜面,小车带动物体以速率沿斜面做匀速直线运动,下列判断正确的是( )
A. 小车的速率为 B. 小车的速率为
C. 小车速率始终大于物体速率 D. 小车做匀变速运动
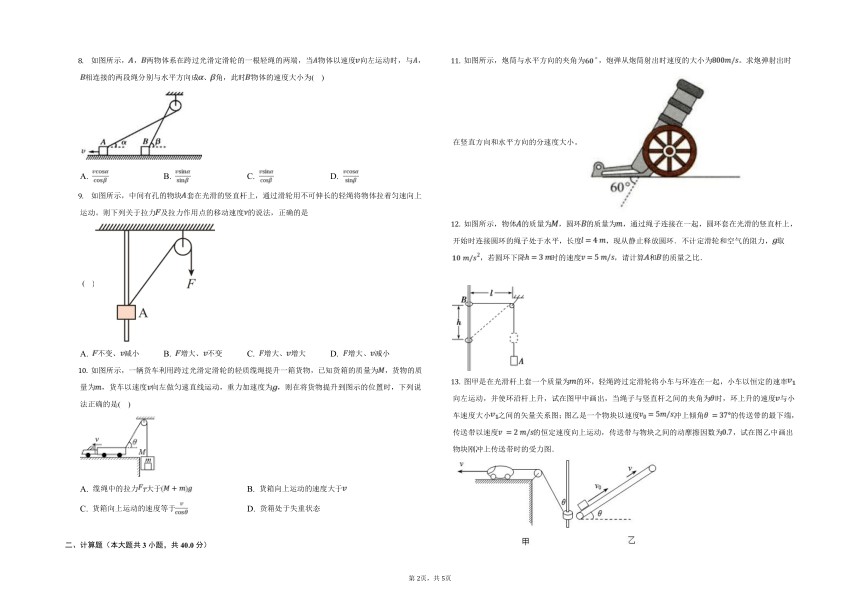
如图所示,,两物体系在跨过光滑定滑轮的一根轻绳的两端,当物体以速度向左运动时,与,相连接的两段绳分别与水平方向成、角,此时物体的速度大小为( )
A. B. C. D.
如图所示,中间有孔的物块套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动。则下列关于拉力及拉力作用点的移动速度的说法,正确的是( )
A. 不变、减小 B. 增大、不变 C. 增大、增大 D. 增大、减小
如图所示,一辆货车利用跨过光滑定滑轮的轻质缆绳提升一箱货物,已知货箱的质量为,货物的质量为,货车以速度向左做匀速直线运动,重力加速度为,则在将货物提升到图示的位置时,下列说法正确的是( )
A. 缆绳中的拉力大于 B. 货箱向上运动的速度大于
C. 货箱向上运动的速度等于 D. 货箱处于失重状态
二、计算题(本大题共3小题,共40.0分)
如图所示,炮筒与水平方向的夹角为,炮弹从炮筒射出时速度的大小为。求炮弹射出时在竖直方向和水平方向的分速度大小。
如图所示,物体的质量为,圆环的质量为,通过绳子连接在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,长度,现从静止释放圆环.不计定滑轮和空气的阻力,取,若圆环下降时的速度,请计算和的质量之比.
图甲是在光滑杆上套一个质量为的环,轻绳跨过定滑轮将小车与环连在一起,小车以恒定的速率向左运动,并使环沿杆上升,试在图甲中画出,当绳子与竖直杆之间的夹角为时,环上升的速度与小车速度大小之间的矢量关系图;图乙是一个物块以速度冲上倾角的传送带的最下端,传送带以速度的恒定速度向上运动,传送带与物块之间的动摩擦因数为,试在图乙中画出物块刚冲上传送带时的受力图.
答案和解析
1.【答案】
【解析】分析:绳子收缩的速度等于人在岸上的速度,连接船的绳子端点既参与了绳子收缩方向上的运动,又参与了绕定滑轮的摆动。根据船的运动速度,结合平行四边形定则求出人拉绳子的速度,及船的加速度。
解决本题的关键知道船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度,并掌握受力分析与理解牛顿第二定律。
解答:
、对小船受力分析,如下图所示,则有,因此船的加速度大小为,故A正确,B错误;
、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度。如图所示根据平行四边形定则有,故CD错误;
故选:。
2.【答案】
【解析】
【分析】
物体以速度沿竖直杆匀速下滑,由于物体沿绳运动,物体的速率等于绳子的速率,将物体的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度等于绳速,由几何知识求解的速率;
本题考查了运动的合成与分解,通常称为绳端物体速度分解问题,关键是知道物体实际运动方向就是速度方向,然后将合速度沿绳子方向和垂直于绳子方向进行分解。
【解答】
将物体的速度按图示两个方向分解,如图所示:
由绳子速率而绳子速率等于物体的速率,则有物体的速率,故B正确,ACD错误;
故选B。
3.【答案】
【解析】将、的速度分解为沿绳的方向和垂直于绳子的方向,两物体沿绳子方向的速度相等,有:
所以:,故B正确,ACD错误。
故选B。
将、的速度分解为沿绳的方向和垂直于绳子的方向,根据两物体沿绳子方向的速度相等,求出的速度。
解决本题的关键会对速度进行分解,难度一般,基础题。
4.【答案】
【解析】
【分析】
根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系。本题考查了学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等。
【解答】
用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从点开始沿铁环运动,根据平行四边形定则得,小球实际速度为:,故A正确。
故选A。
5.【答案】
【解析】
【分析】
将球的运动分解为沿杆子方向和垂直于杆子方向,抓住沿杆子方向速度相等得出、的速度关系,结合系统机械能守恒求出此时、的速度。
解决本题的关键知道系统机械能守恒,抓住两球沿杆子方向的速度相等,进行求解。
【解答】
小球沿墙下滑距离为时,设此时球的速度为,球的速度为
根据系统机械能守恒定律得:
两球沿杆子方向上的速度相等,则有:
联立两式解得:, 故C正确,ABD错误。
故选C。
6.【答案】
【解析】
【分析】
本题主要考查牵连速度问题,运动的合成和分解。
将的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的速度等于的速度大小,据此解答即可。
【解答】
将的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的速度等于的速度大小,有,解得,故B正确,ACD错误。
故选B。
7.【答案】
【解析】
【分析】
先对小车的速度进行分解,分解成沿绳子方向的速度和垂直于绳子方向的速度,根据沿绳子方向的速度大小等于物体的速度大小,即可求解。
解题的关键是关于牵连速度的问题,注意速度的分解先找出合速度,然后进行速度的分解,找出两物体的牵连速度。
【解答】
将小车的速度进行分解如图所示,
则,故A、B错误;
物体速度,,随着小车向右运动,变小,由于物体速度不变,故小车做加速运动,且为非匀变速运动,故C正确,D错误。
故选C。
8.【答案】
【解析】
【分析】
关键是找到沿绳方向的速度大小相等,分别对、物体速度沿着绳子方向与垂直绳子方向进行分解,根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系。
本题考查了学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等。
【解答】
对物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为;对物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为,由于沿着绳子方向速度大小相等,所以则有,因此,故BCD错误,A正确。
故选A。
9.【答案】
【解析】设绳子与竖直方向上的夹角为,因为做匀速直线运动,在竖直方向上合力为零,有:,因为增大,则增大.
设拉力作用点的移动速度,物体向上运动的速度为,则
由于恒定,因为增大,则减小
故D正确,ABC错误。
故选D。
10.【答案】
【解析】
【分析】
由于绳子不可伸长,货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等,根据平行四边形定则求解出货箱和货物整体向上运动的速度表达式进行分析即可。
本题关键先推导出货箱和货物整体的速度表达式,确定货箱和货物整体的运动规律,然后超重与失重的特点分析,不难。
【解答】
将货车的速度进行正交分解,如图所示:
由于绳子不可伸长,货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等,故:
由于不断减小,故货箱和货物整体向上做加速运动,加速度向上;
B.货箱和货物整体向上做加速运动,大小小于,故B错误;
A.货箱和货物整体向上做加速运动,故拉力大于,故A正确;
C.货箱的速度为,故C错误;
D.货箱和货物整体向上做加速运动,加速度向上,是超重,故D错误。
故选A。
11.【答案】解:将炮弹的速度在竖直方向和水平方向进行分解,得
【解析】见答案
12.【答案】解:
若圆环下降时的速度,由机械能守恒定律得:
如图所示:由几何关系得:上升的高度
、的速度关系为:
解得:
【解析】将物体的速度沿绳和垂直于绳方向进行分解。、和绳子组成的系统机械能守恒,再结合几何关系列式求解。
本题是运动的合成和分解及机械能守恒定律的综合题目,中等难度。
13.【答案】,。
【解析】略
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,人在岸上拉船,已知船的质量为,水的阻力恒为,当轻绳与水平面的夹角为时,船的速度为,此时人的拉力大小为,则( )
A. 船的加速度为 B. 船的加速度为
C. 人拉绳行走的速度为 D. 人拉绳行走的速度为
如图所示,物体以速度沿杆匀速下滑,用细绳通过定滑轮拉物体,当绳与水平夹角为时,的速度为( )
A. B. C. D.
如下图所示,有一竖直放置的“”形架,表面光滑,滑块、分别套在水平杆与竖直杆上,、用一不可伸长的轻细绳相连,、质量相等,且可看作质点,开始时细绳水平伸直,、静止.由静止释放后,已知当细绳与竖直方向的夹角为时,滑块沿着竖直杆下滑的速度大小为,则此时的速度大小为( )
A. B. C. D.
固定在竖直平面内的半圆形刚性铁环,半径为,铁环上穿着小球,铁环圆心的正上方固定一个小定滑轮。用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从点开始沿铁环运动,某时刻角度关系如下图所示,若绳末端速度为则小球此时的速度为( )
A. B. C. D.
一个长直轻杆两端分别固定一个小球和,两小球质量均为,大小忽略不计,杆的长度为。先将杆竖直靠放在竖直墙上,如图所示,轻轻振动小球,使小球在水平面上由静止开始向右滑动,当小球沿墙下滑距离为时,下列说法正确的是不计一切摩擦( )
A. 小球和的速度都为 B. 小球和的速度都为
C. 小球、的速度分别为和 D. 小球、的速度分别为和
如图所示,轻绳跨过两个光滑定滑轮连接物块和,其中物块套在水平杆上。图示位置,细线与水平杆的夹角,的速度方向向右,大小为。则物块的速度大小为
A. B. C. D.
质量为的物体置于倾角为的固定光滑斜面上,斜面足够长,轻细绳跨过光滑定滑轮分别连接着与动力小车,与滑轮间的细绳平行于斜面,小车带动物体以速率沿斜面做匀速直线运动,下列判断正确的是( )
A. 小车的速率为 B. 小车的速率为
C. 小车速率始终大于物体速率 D. 小车做匀变速运动
如图所示,,两物体系在跨过光滑定滑轮的一根轻绳的两端,当物体以速度向左运动时,与,相连接的两段绳分别与水平方向成、角,此时物体的速度大小为( )
A. B. C. D.
如图所示,中间有孔的物块套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动。则下列关于拉力及拉力作用点的移动速度的说法,正确的是( )
A. 不变、减小 B. 增大、不变 C. 增大、增大 D. 增大、减小
如图所示,一辆货车利用跨过光滑定滑轮的轻质缆绳提升一箱货物,已知货箱的质量为,货物的质量为,货车以速度向左做匀速直线运动,重力加速度为,则在将货物提升到图示的位置时,下列说法正确的是( )
A. 缆绳中的拉力大于 B. 货箱向上运动的速度大于
C. 货箱向上运动的速度等于 D. 货箱处于失重状态
二、计算题(本大题共3小题,共40.0分)
如图所示,炮筒与水平方向的夹角为,炮弹从炮筒射出时速度的大小为。求炮弹射出时在竖直方向和水平方向的分速度大小。
如图所示,物体的质量为,圆环的质量为,通过绳子连接在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,长度,现从静止释放圆环.不计定滑轮和空气的阻力,取,若圆环下降时的速度,请计算和的质量之比.
图甲是在光滑杆上套一个质量为的环,轻绳跨过定滑轮将小车与环连在一起,小车以恒定的速率向左运动,并使环沿杆上升,试在图甲中画出,当绳子与竖直杆之间的夹角为时,环上升的速度与小车速度大小之间的矢量关系图;图乙是一个物块以速度冲上倾角的传送带的最下端,传送带以速度的恒定速度向上运动,传送带与物块之间的动摩擦因数为,试在图乙中画出物块刚冲上传送带时的受力图.
答案和解析
1.【答案】
【解析】分析:绳子收缩的速度等于人在岸上的速度,连接船的绳子端点既参与了绳子收缩方向上的运动,又参与了绕定滑轮的摆动。根据船的运动速度,结合平行四边形定则求出人拉绳子的速度,及船的加速度。
解决本题的关键知道船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度,并掌握受力分析与理解牛顿第二定律。
解答:
、对小船受力分析,如下图所示,则有,因此船的加速度大小为,故A正确,B错误;
、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度。如图所示根据平行四边形定则有,故CD错误;
故选:。
2.【答案】
【解析】
【分析】
物体以速度沿竖直杆匀速下滑,由于物体沿绳运动,物体的速率等于绳子的速率,将物体的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度等于绳速,由几何知识求解的速率;
本题考查了运动的合成与分解,通常称为绳端物体速度分解问题,关键是知道物体实际运动方向就是速度方向,然后将合速度沿绳子方向和垂直于绳子方向进行分解。
【解答】
将物体的速度按图示两个方向分解,如图所示:
由绳子速率而绳子速率等于物体的速率,则有物体的速率,故B正确,ACD错误;
故选B。
3.【答案】
【解析】将、的速度分解为沿绳的方向和垂直于绳子的方向,两物体沿绳子方向的速度相等,有:
所以:,故B正确,ACD错误。
故选B。
将、的速度分解为沿绳的方向和垂直于绳子的方向,根据两物体沿绳子方向的速度相等,求出的速度。
解决本题的关键会对速度进行分解,难度一般,基础题。
4.【答案】
【解析】
【分析】
根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系。本题考查了学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等。
【解答】
用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从点开始沿铁环运动,根据平行四边形定则得,小球实际速度为:,故A正确。
故选A。
5.【答案】
【解析】
【分析】
将球的运动分解为沿杆子方向和垂直于杆子方向,抓住沿杆子方向速度相等得出、的速度关系,结合系统机械能守恒求出此时、的速度。
解决本题的关键知道系统机械能守恒,抓住两球沿杆子方向的速度相等,进行求解。
【解答】
小球沿墙下滑距离为时,设此时球的速度为,球的速度为
根据系统机械能守恒定律得:
两球沿杆子方向上的速度相等,则有:
联立两式解得:, 故C正确,ABD错误。
故选C。
6.【答案】
【解析】
【分析】
本题主要考查牵连速度问题,运动的合成和分解。
将的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的速度等于的速度大小,据此解答即可。
【解答】
将的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的速度等于的速度大小,有,解得,故B正确,ACD错误。
故选B。
7.【答案】
【解析】
【分析】
先对小车的速度进行分解,分解成沿绳子方向的速度和垂直于绳子方向的速度,根据沿绳子方向的速度大小等于物体的速度大小,即可求解。
解题的关键是关于牵连速度的问题,注意速度的分解先找出合速度,然后进行速度的分解,找出两物体的牵连速度。
【解答】
将小车的速度进行分解如图所示,
则,故A、B错误;
物体速度,,随着小车向右运动,变小,由于物体速度不变,故小车做加速运动,且为非匀变速运动,故C正确,D错误。
故选C。
8.【答案】
【解析】
【分析】
关键是找到沿绳方向的速度大小相等,分别对、物体速度沿着绳子方向与垂直绳子方向进行分解,根据三角函数关系及沿着绳子方向速度大小相等,可知两物体的速度大小关系。
本题考查了学会对物体进行运动的分解,涉及到平行四边形定则与三角函数知识,同时本题的突破口是沿着绳子的方向速度大小相等。
【解答】
对物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为;对物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为,由于沿着绳子方向速度大小相等,所以则有,因此,故BCD错误,A正确。
故选A。
9.【答案】
【解析】设绳子与竖直方向上的夹角为,因为做匀速直线运动,在竖直方向上合力为零,有:,因为增大,则增大.
设拉力作用点的移动速度,物体向上运动的速度为,则
由于恒定,因为增大,则减小
故D正确,ABC错误。
故选D。
10.【答案】
【解析】
【分析】
由于绳子不可伸长,货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等,根据平行四边形定则求解出货箱和货物整体向上运动的速度表达式进行分析即可。
本题关键先推导出货箱和货物整体的速度表达式,确定货箱和货物整体的运动规律,然后超重与失重的特点分析,不难。
【解答】
将货车的速度进行正交分解,如图所示:
由于绳子不可伸长,货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等,故:
由于不断减小,故货箱和货物整体向上做加速运动,加速度向上;
B.货箱和货物整体向上做加速运动,大小小于,故B错误;
A.货箱和货物整体向上做加速运动,故拉力大于,故A正确;
C.货箱的速度为,故C错误;
D.货箱和货物整体向上做加速运动,加速度向上,是超重,故D错误。
故选A。
11.【答案】解:将炮弹的速度在竖直方向和水平方向进行分解,得
【解析】见答案
12.【答案】解:
若圆环下降时的速度,由机械能守恒定律得:
如图所示:由几何关系得:上升的高度
、的速度关系为:
解得:
【解析】将物体的速度沿绳和垂直于绳方向进行分解。、和绳子组成的系统机械能守恒,再结合几何关系列式求解。
本题是运动的合成和分解及机械能守恒定律的综合题目,中等难度。
13.【答案】,。
【解析】略
第1页,共1页
