人教版数学九上24.4.1弧长和扇形面积 课件(18张PPT)
文档属性
| 名称 | 人教版数学九上24.4.1弧长和扇形面积 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 639.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
人教版 九年级上
24.4 弧长和扇形的面积
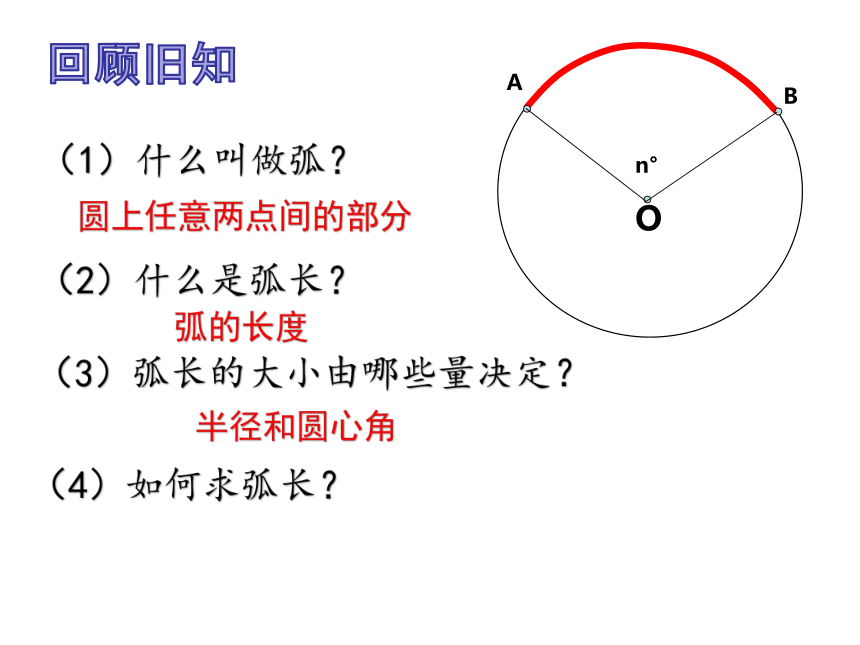
回顾旧知
(1)什么叫做弧?
(2)什么是弧长?
(3)弧长的大小由哪些量决定?
(4)如何求弧长?
A
B
O
圆上任意两点间的部分
弧的长度
半径和圆心角
n°
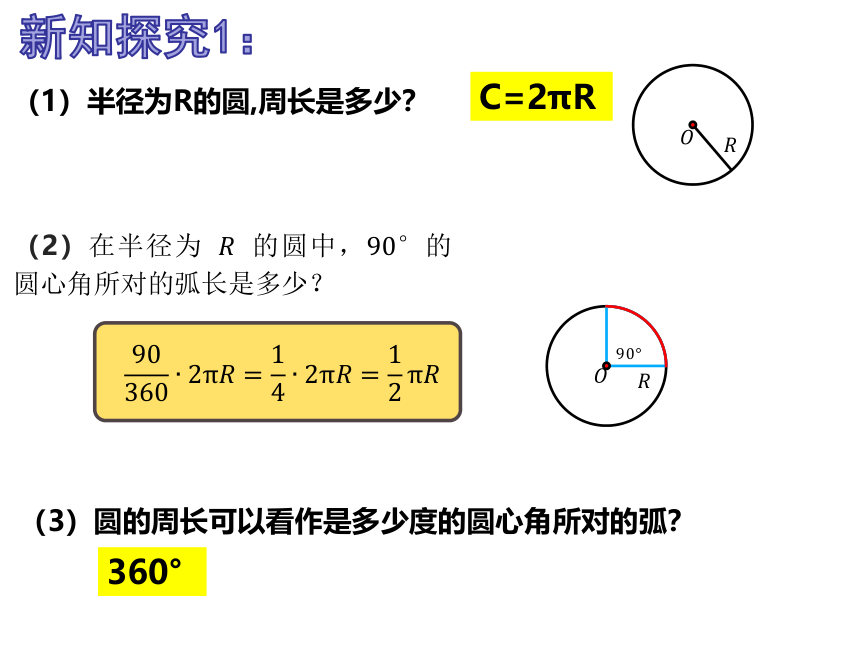
(1)半径为R的圆,周长是多少?
C=2πR
(3)圆的周长可以看作是多少度的圆心角所对的弧?
360°
新知探究1:
(2)在半径为 的圆中,的圆心角所对的弧长是多少?
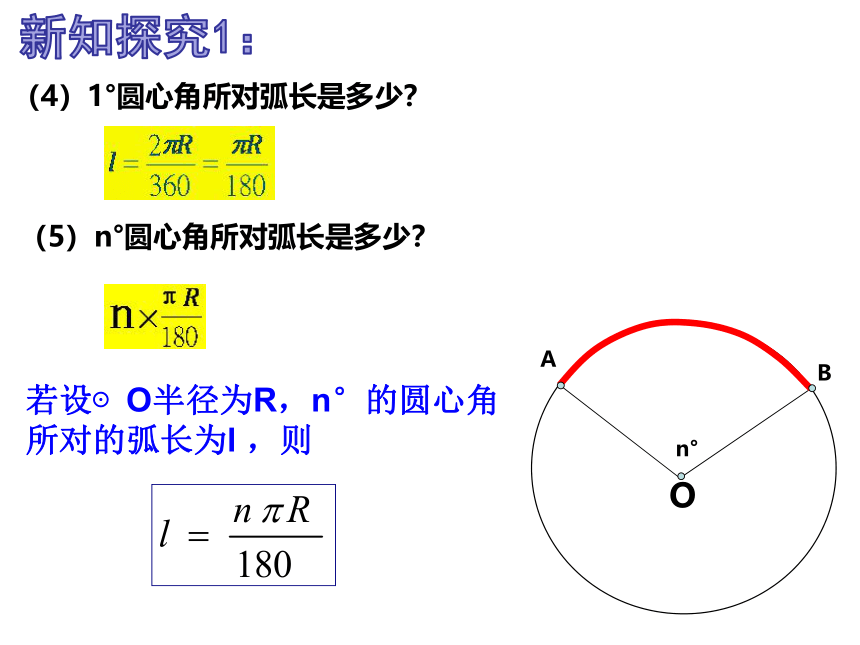
(4)1°圆心角所对弧长是多少?
n°
A
B
O
(5)n°圆心角所对弧长是多少?
若设⊙O半径为R,n°的圆心角所对的弧长为l ,则
新知探究1:
跟踪练习1
1.已知弧所对的圆心角为900,半径是4,则弧长为 .
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 .
160°
跟踪练习1
3.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
B
小结:弧长公式涉及三个量 :
1.弧长; 2.半径; 3.圆心角的度数;
知道其中两个量,就可以求第三个量。
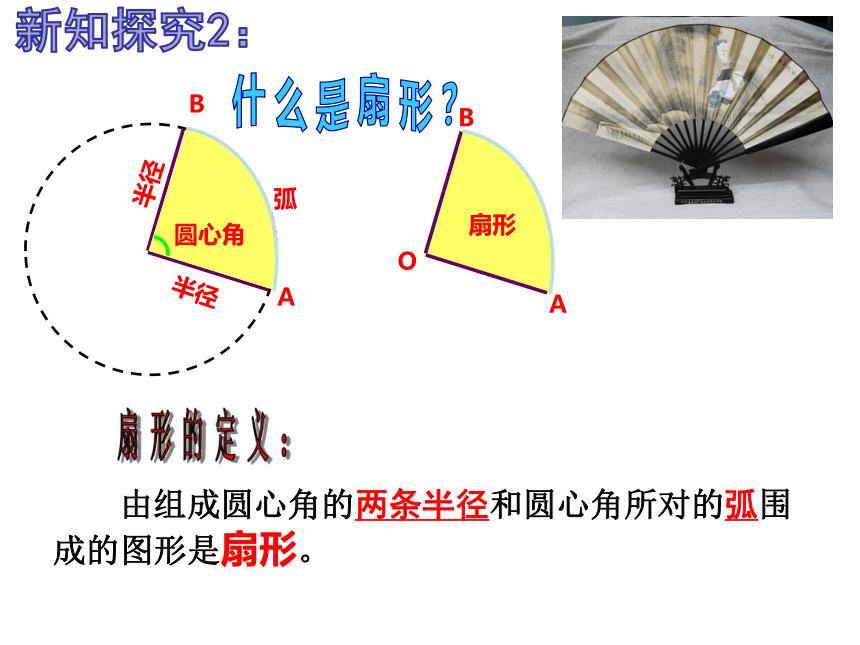
什 么 是 扇 形 ?
扇 形 的 定 义 :
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
新知探究2:
什 么 是 扇 形 ?
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
问题:(1)扇形的面积由哪些量决定?
(2)如何求扇形的面积?
半径和圆心角
新知探究2:
360°
(1) 如果圆的半径为R,则圆的面积为多少?
(2) 圆的面积可以看成多少度圆心角扇形的面积?
新知探究3:
A
B
O
在半径为R 的圆中,圆心角为n°的扇形面积的计算公式为:
(3) 圆心角为1°的扇形面积为多少?
(4) 圆心角为n°的扇形面积为多少?
新知探究3:
A
B
O
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
想一想:扇形的面积公式 与什么公式类似?
知识联系:
三角形面积公式
3、已知扇形的圆心角为150°,弧长为 ,则扇形的面积为____________.
2、已知扇形的圆心角为30°,面积为 ,则这个扇形的半径R=_________.
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.
6cm
小结:扇形面积公式涉及三个量:
1.扇形面积; 2.半径; 3.圆心角的度数 ;
知道其中两个量,就可以求第三个量。
跟踪练习2
例:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.
0
B
A
C
D
S弓形= S扇形- S△
典例讲解:
如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
0
A
B
D
C
E
变式训练:
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
巩固练习:
1.如图,四边形ABCD是☉O的内接四边形,☉O的半径为4,∠B=135°,则弧AC的长为( )
A. B.
C. D.
2.如图,△ABC内接于圆O,∠B=65°,∠C=70°,若BC= ,则弧BC的长为( )
A. B.
C. D.
C
A
3.如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是( )
A. B.
C. D.
4.如图,在平行四边形ABCD中,ABA. B.
C. D.
C
A
如图,一根 长 的绳子,一端栓在柱子上,另一端栓着一只羊, 羊的活动最大区域 .
5
趣味数学
3m
5m
课堂小结:
1.本节课我们学习了什么知识呢?
2.我们是如何推导出两个公式的?
人教版 九年级上
24.4 弧长和扇形的面积
回顾旧知
(1)什么叫做弧?
(2)什么是弧长?
(3)弧长的大小由哪些量决定?
(4)如何求弧长?
A
B
O
圆上任意两点间的部分
弧的长度
半径和圆心角
n°
(1)半径为R的圆,周长是多少?
C=2πR
(3)圆的周长可以看作是多少度的圆心角所对的弧?
360°
新知探究1:
(2)在半径为 的圆中,的圆心角所对的弧长是多少?
(4)1°圆心角所对弧长是多少?
n°
A
B
O
(5)n°圆心角所对弧长是多少?
若设⊙O半径为R,n°的圆心角所对的弧长为l ,则
新知探究1:
跟踪练习1
1.已知弧所对的圆心角为900,半径是4,则弧长为 .
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 .
160°
跟踪练习1
3.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
B
小结:弧长公式涉及三个量 :
1.弧长; 2.半径; 3.圆心角的度数;
知道其中两个量,就可以求第三个量。
什 么 是 扇 形 ?
扇 形 的 定 义 :
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
新知探究2:
什 么 是 扇 形 ?
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
问题:(1)扇形的面积由哪些量决定?
(2)如何求扇形的面积?
半径和圆心角
新知探究2:
360°
(1) 如果圆的半径为R,则圆的面积为多少?
(2) 圆的面积可以看成多少度圆心角扇形的面积?
新知探究3:
A
B
O
在半径为R 的圆中,圆心角为n°的扇形面积的计算公式为:
(3) 圆心角为1°的扇形面积为多少?
(4) 圆心角为n°的扇形面积为多少?
新知探究3:
A
B
O
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
想一想:扇形的面积公式 与什么公式类似?
知识联系:
三角形面积公式
3、已知扇形的圆心角为150°,弧长为 ,则扇形的面积为____________.
2、已知扇形的圆心角为30°,面积为 ,则这个扇形的半径R=_________.
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.
6cm
小结:扇形面积公式涉及三个量:
1.扇形面积; 2.半径; 3.圆心角的度数 ;
知道其中两个量,就可以求第三个量。
跟踪练习2
例:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.
0
B
A
C
D
S弓形= S扇形- S△
典例讲解:
如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
0
A
B
D
C
E
变式训练:
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
巩固练习:
1.如图,四边形ABCD是☉O的内接四边形,☉O的半径为4,∠B=135°,则弧AC的长为( )
A. B.
C. D.
2.如图,△ABC内接于圆O,∠B=65°,∠C=70°,若BC= ,则弧BC的长为( )
A. B.
C. D.
C
A
3.如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是( )
A. B.
C. D.
4.如图,在平行四边形ABCD中,AB
C. D.
C
A
如图,一根 长 的绳子,一端栓在柱子上,另一端栓着一只羊, 羊的活动最大区域 .
5
趣味数学
3m
5m
课堂小结:
1.本节课我们学习了什么知识呢?
2.我们是如何推导出两个公式的?
同课章节目录
