人教版新教材必修二 5.4 抛体运动的规律抛体临界专题(含答案)
文档属性
| 名称 | 人教版新教材必修二 5.4 抛体运动的规律抛体临界专题(含答案) | 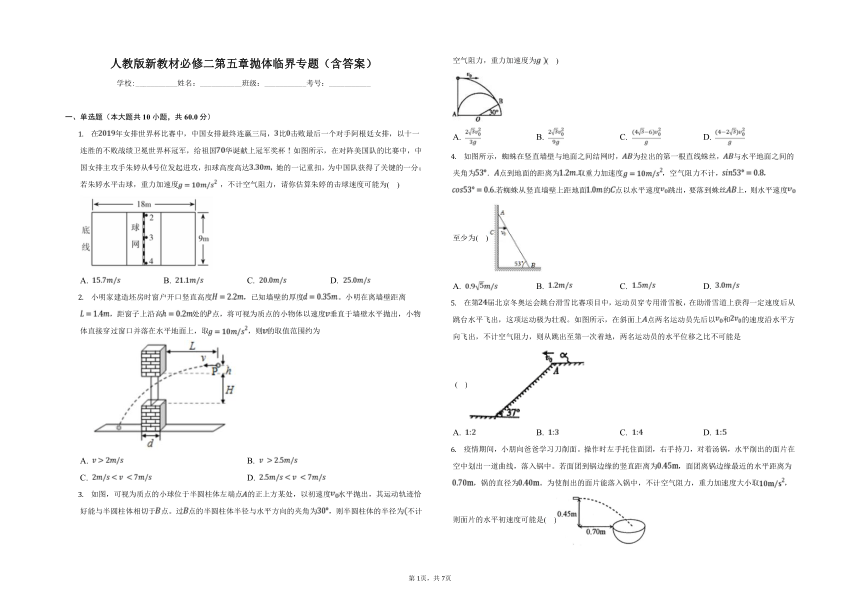 | |
| 格式 | zip | ||
| 文件大小 | 723.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-26 12:54:29 | ||
图片预览



文档简介
人教版新教材必修二第五章抛体临界专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
在年女排世界杯比赛中,中国女排最终连赢三局,比击败最后一个对手阿根廷女排,以十一连胜的不败战绩卫冕世界杯冠军,给祖国华诞献上冠军奖杯如图所示,在对阵美国队的比赛中,中国女排主攻手朱婷从号位发起进攻,扣球高度高达,她的一记重扣,为中国队获得了关键的一分;若朱婷水平击球,重力加速度,不计空气阻力,请你估算朱婷的击球速度可能为( )
A. B. C. D.
小明家建造坯房时窗户开口竖直高度,已知墙壁的厚度。小明在离墙壁距离,距窗子上沿高处的点,将可视为质点的小物体以速度垂直于墙壁水平抛出,小物体直接穿过窗口并落在水平地面上,取,则的取值范围约为
A. B.
C. D.
如图,可视为质点的小球位于半圆柱体左端点的正上方某处,以初速度水平抛出,其运动轨迹恰好能与半圆柱体相切于点。过点的半圆柱体半径与水平方向的夹角为,则半圆柱体的半径为不计空气阻力,重力加速度为( )
A. B. C. D.
如图所示,蜘蛛在竖直墙壁与地面之间结网时,为拉出的第一根直线蛛丝,与水平地面之间的夹角为.点到地面的距离为取重力加速度,空气阻力不计,,若蜘蛛从竖直墙壁上距地面的点以水平速度跳出,要落到蛛丝上,则水平速度至少为( )
A. B. C. D.
在第届北京冬奥运会跳台滑雪比赛项目中,运动员穿专用滑雪板,在助滑雪道上获得一定速度后从跳台水平飞出,这项运动极为壮观。如图所示,在斜面上点两名运动员先后以和的速度沿水平方向飞出,不计空气阻力,则从跳出至第一次着地,两名运动员的水平位移之比不可能是( )
A. B. C. D.
疫情期间,小朋向爸爸学习刀削面。操作时左手托住面团,右手持刀,对着汤锅,水平削出的面片在空中划出一道曲线,落入锅中。若面团到锅边缘的竖直距离为,面团离锅边缘最近的水平距离为,锅的直径为。为使削出的面片能落入锅中,不计空气阻力,重力加速度大小取,则面片的水平初速度可能是( )
A. B. C. D.
如图所示为一乒乓球发球机的简易图,假设发球机在球网中点的正上方离桌面高处以不同的初速度沿水平方向发出,且每次乒乓球均能落在台面上.已知球台为边长为的正方形,重力加速度为,忽略空气的阻力.则下列说法正确的是
A. 只有水平向右发射的乒乓球,在空中下落的时间为
B. 乒乓球的最大位移为
C. 乒乓球从发射到落在台面上的位移与乒乓球的质量有关
D. 乒乓球最大的初速度为
一阶梯如图所示,其中每级台阶的高度和宽度都是,一小球以水平速度飞出,欲打在第四级台阶上,则的取值范围是
A. B.
C. D.
如图为湖边一倾角为的大坝的横截面示意图,水面与大坝的交点为。一人站在点处以速度沿水平方向扔小石子,已知,取。下列说法正确的是( )
A. 若,则石块可以落入水中
B. 若石块能落入水中,则越大,落水时速度方向与水平面的夹角越大
C. 若石块不能落入水中,则越大,落到斜面上时速度方向与斜面的夹角越大
D. 若石块不能落入水中,则越大,落到斜面上时速度方向与斜面的夹角越小
如图所示,,两个平台水平距离为某同学先用一个小球从平台边缘以的速度水平抛出,结果小球落在了平台左侧下方处.取,忽略空气阻力.要使小球从平台边缘水平抛出能落到平台上,则从平台边缘水平抛出小球的速度至少为( )
A. B. C. D.
二、计算题(本大题共3小题,共40.0分)
如图所示,投壶是我国古代的一种投掷游戏,也是一种礼仪.据礼记投壶记载,以盛酒的壶口作为标的,在一定的距离内投箭矢,以投入多少决胜负,负者罚酒.儒家所奉行的“六艺”,即“礼、乐、射、御、书、数”,而投壶就来自于这六艺之一.现在有甲、乙两人进行投壶游戏,为简化起见,将箭矢视为质点球,并且不计空气阻力.如图所示,甲从离地面高的点以初速度水平抛出质点球,质点球正好落在壶口点,不计壶的高度.乙从离地面高的点水平抛出质点球,如果也要使质点球落到壶口点,则他抛球的初速度应该是多大?已知重力加速度
如图所示,水平屋顶高,墙高,墙到房子的距离,墙外马路宽,小球从房顶点水平飞出,取
若小球落在墙外的马路上,求小球在空中运动的时间;
若小球恰好经过墙顶点后落在马路上,求小球离开房顶时的速度;
若小球落在墙外的马路上,求小球离开房顶时的速度的取值范围。
如图所示,挡板与竖直方向所夹的锐角为,一小球视为质点从点正下方点以速度水平抛出,小球运动过程中恰好不和挡板碰撞小球轨迹所在平面与挡板垂直。不计空气阻力,重力加速度大小为,求
小球恰好不和挡板碰撞时的竖直速度大小。
、间的距离。
答案和解析
1.【答案】
【解析】解:根据得下落得时间为:,
从号位击球,当球恰好沿对角线落在界内时,速度最大,此时水平方向的位移为:
则击球的最大初速度为:。
所以:故A正确,BCD错误
故选:。
根据击球点与网的高度差求出球平抛运动的时间,结合击球点与网之间的水平距离求出球的最小初速度,根据击球点的高度求出平抛运动的时间,结合击球点与底线的水平距离求出球的最大初速度。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界情况,结合运动学公式灵活求解,难度不大。
2.【答案】
【解析】
【分析】
小物体做平抛运动,恰好擦着窗子上沿右侧穿过时最大。恰好擦着窗口下沿左侧时速度最小,由分位移公式求解。
解决本题的关键明确临界条件,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活解答。
【解答】
小物体做平抛运动,恰好擦着窗子上沿右侧穿过时最大。此时有 ,
代入解得:
恰好擦着窗口下沿左侧时速度最小,则有 ,
解得:
故的取值范围是,故ABC错误,D正确。
故选D。
3.【答案】
【解析】在点,据题可知小球的速度方向与水平方向成角,由速度的分解可知,竖直分速度大小为:
得:
故选:。
根据题意小球飞行过程中恰好与半圆轨道相切于点,可知速度的方向与水平方向成角,根据速度方向得到在点竖直分速度的大小,再根据平抛运动的规律和几何知识结合即可求解半圆柱体的半径。
解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,抓住速度方向,结合位移关系、速度关系进行求解。
4.【答案】
【解析】
【分析】
利用数学的几何关系可知,要到达蛛丝,那么蜘蛛到达蜘蛛网的速度恰好与水平方向成时初速度最小,再利用平抛运动的物理公式联立求解。
平抛运动和斜面的结合,而又不同于常规的考法,题目偏新颖,但解题方法依然是平抛运动和几何关系的综合应用,很好地让学生在模型迁移中得到成长。
【解答】
分析题意可知,蜘蛛到达蜘蛛网的时候速度与水平方向成时初速度最小,假设时间为,,,则,再根据几何关系知,根据平抛运动的规律知:,,
联立以上式子,解得,故ABD错误,C正确。
5.【答案】
【解析】
【分析】
若两名运动员都落地斜面上,则,得出水平位移之比;若两名运动员都落到水平地面上,根据可知,时间相等,再根据水平方向的运动分解水平位移之比。
本题是平抛运动和斜面相结合的问题,基础题目。
【解答】
设水平位移为,竖直位移为,两位运动员分别为、,若都落在斜面上,根据
即为
可得
根据
可得
当都落在水平面上时,由可知,运动时间相等,则,
综合上述可知,两名运动员水平位移之比最小为,故D不可能,故ABC均正确;
本题选择不可能的,故选D。
6.【答案】
【解析】
【分析】
平抛运动研究方法是分解成水平方向的匀速直线运动和竖直方向的自由落体运动两个分运动,两个分运动具有等时性,根据分运动公式即可求解。
本题考查平抛运动基本知识,需对平抛运动水平竖直两个方向得运动公式熟练掌握,解题时要注意取值范围和多解问题。
【解答】
根据,代入数据得:
由题意知水平位移最大为:,最小为:
根据代入数据得:,只有符合题意;
故选C。
7.【答案】
【解析】
【分析】
本题主要是考查了平抛运动的规律,知道平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;
解决本题的关键知道分运动和合运动具有等时性,知道平抛运动的时间由高度决定,与初速度、物体的质量等无关。
平抛运动的时间由高度决定;根据几何关系求解最大位移;位移大小与质量无关;
水平位移最大时初速度最大,根据平抛运动规律求解最大初速度。
【解答】
A.无论沿哪个方向平抛,运动时间都相同,根据可得在空中下落的时间为,故A错误;
B.从抛出点到右侧角时位移最大,故最大位移为,故B错误;
C.乒乓球从发射到落在台面上的位移大小与乒乓球的质量无关,故C错误;
D.乒乓球的最大水平位移为,乒乓球的最大初速度为,故D正确。
故选D。
8.【答案】
【解析】
【分析】
本题考查了平抛运动;解决本题的关键明确平抛运动的解决方法,掌握临界情况,速度最小时落在第三级台阶的边缘上,速度最大时落在第四级台阶边缘上。
小球以水平速度由第一级台阶上抛出欲打在第四级台阶上,求出两个临界情况,速度最小时打在第三级台阶的边缘上,速度最大时,打在第四级台阶的边缘上.根据和,得出的临界值。
【解答】
若小球打在第四级台阶的边缘上高度,根据,得;
水平位移则平抛的最大速度;
若小球打在第三级台阶的边缘上,高度,根据,得;
水平位移,则平抛运动的最小速度;
所以速度范围:;
故A正确,BCD错误。
故选A。
9.【答案】
【解析】
【分析】
根据平抛规律和推论逐一分析即可。
本题考查了平抛运动与斜面的结合,熟悉平抛运动规律是解题的关键。
【解答】
A.若石块恰能落到点,,则,,解得,,所以若,则石块可以落入水中,故A正确;
B.因为石块落水的时间均为,落到水中的竖直速度,由,可知石块能落入水中时,越大,落水时速度方向与水平面的夹角越小,故B错误;
C.若石块不能落入水中,则落到斜面上时位移方向与水平方向的夹角即位移偏转角恒为,由速度偏转角与位移偏转角关系满足,即速度偏转角为定值,落到斜面上时速度方向与斜面的夹角为定值,故CD错误。
故选A。
10.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度差求出即可。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,由运动学公式解答。
【解答】
由平抛运动的规律可知:;;
当小球恰能落到平台上时:;;
联立解得:;故B正确、ACD错误。
故选:。
11.【答案】解:设甲抛出的质点球做平抛运动的水平距离为,
则对甲抛出的质点球有 ,
联立解得
对乙抛出的质点球有 ,
联立解得.
【解析】同答案
12.【答案】解:根据得,小球在空中运动的时间.
设小球运动到墙顶点所用时间为
竖直方向上有:,
水平方向上有:
代入数据解得
最小时,小球恰好经过墙顶点后落在马路上,最大时,小球落在马路的最右端.
设的最大值为
竖直方向上有:
水平方向上有:
代入数据解得
所以小球抛出时的速度取值范围大小为 .
答:小球在空中运动的时间为;
小球离开房顶时的速度为;
小球离开房顶时的速度的取值范围为 .
【解析】根据高度出小球在空中运动的时间.
根据下降的高度求出平抛运动的时间,结合水平位移和时间求出小球离开房顶的速度.
抓住小球刚好经过墙顶以及小球刚好不落在马路上,结合两个临界状态,根据平抛运动的规律求出小球离开房顶的初速度取值范围.
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界状态,结合运动学公式灵活求解,难度不大.
13.【答案】解:由于小球恰好不和挡板碰撞,到达挡板时,速度方向与恰好平行,
则有:
解得:;
根据得,运动的时间为:
则小球做平抛运动的水平位移为:
竖直位移为:
设、间的距离为,由几何关系得:
联立解得:。
答:小球恰好不和挡板碰撞时的竖直速度大小为;
、间的距离为。
【解析】解决本题的关键是知道平抛运动在水平方向和竖直方向上的运动规律,明确小球恰好不和挡板碰撞的临界条件是速度方向与挡板平行,结合运动学公式和几何关系综合求解。
根据小球恰好不和挡板碰撞,达到挡板时,速度方向与挡板恰好平行,结合平行四边形定则求出竖直分速度的大小;
根据速度的关系求出平抛运动的时间,从而求出平抛运动的水平位移和竖直位移,结合几何关系求出间的距离。
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
在年女排世界杯比赛中,中国女排最终连赢三局,比击败最后一个对手阿根廷女排,以十一连胜的不败战绩卫冕世界杯冠军,给祖国华诞献上冠军奖杯如图所示,在对阵美国队的比赛中,中国女排主攻手朱婷从号位发起进攻,扣球高度高达,她的一记重扣,为中国队获得了关键的一分;若朱婷水平击球,重力加速度,不计空气阻力,请你估算朱婷的击球速度可能为( )
A. B. C. D.
小明家建造坯房时窗户开口竖直高度,已知墙壁的厚度。小明在离墙壁距离,距窗子上沿高处的点,将可视为质点的小物体以速度垂直于墙壁水平抛出,小物体直接穿过窗口并落在水平地面上,取,则的取值范围约为
A. B.
C. D.
如图,可视为质点的小球位于半圆柱体左端点的正上方某处,以初速度水平抛出,其运动轨迹恰好能与半圆柱体相切于点。过点的半圆柱体半径与水平方向的夹角为,则半圆柱体的半径为不计空气阻力,重力加速度为( )
A. B. C. D.
如图所示,蜘蛛在竖直墙壁与地面之间结网时,为拉出的第一根直线蛛丝,与水平地面之间的夹角为.点到地面的距离为取重力加速度,空气阻力不计,,若蜘蛛从竖直墙壁上距地面的点以水平速度跳出,要落到蛛丝上,则水平速度至少为( )
A. B. C. D.
在第届北京冬奥运会跳台滑雪比赛项目中,运动员穿专用滑雪板,在助滑雪道上获得一定速度后从跳台水平飞出,这项运动极为壮观。如图所示,在斜面上点两名运动员先后以和的速度沿水平方向飞出,不计空气阻力,则从跳出至第一次着地,两名运动员的水平位移之比不可能是( )
A. B. C. D.
疫情期间,小朋向爸爸学习刀削面。操作时左手托住面团,右手持刀,对着汤锅,水平削出的面片在空中划出一道曲线,落入锅中。若面团到锅边缘的竖直距离为,面团离锅边缘最近的水平距离为,锅的直径为。为使削出的面片能落入锅中,不计空气阻力,重力加速度大小取,则面片的水平初速度可能是( )
A. B. C. D.
如图所示为一乒乓球发球机的简易图,假设发球机在球网中点的正上方离桌面高处以不同的初速度沿水平方向发出,且每次乒乓球均能落在台面上.已知球台为边长为的正方形,重力加速度为,忽略空气的阻力.则下列说法正确的是
A. 只有水平向右发射的乒乓球,在空中下落的时间为
B. 乒乓球的最大位移为
C. 乒乓球从发射到落在台面上的位移与乒乓球的质量有关
D. 乒乓球最大的初速度为
一阶梯如图所示,其中每级台阶的高度和宽度都是,一小球以水平速度飞出,欲打在第四级台阶上,则的取值范围是
A. B.
C. D.
如图为湖边一倾角为的大坝的横截面示意图,水面与大坝的交点为。一人站在点处以速度沿水平方向扔小石子,已知,取。下列说法正确的是( )
A. 若,则石块可以落入水中
B. 若石块能落入水中,则越大,落水时速度方向与水平面的夹角越大
C. 若石块不能落入水中,则越大,落到斜面上时速度方向与斜面的夹角越大
D. 若石块不能落入水中,则越大,落到斜面上时速度方向与斜面的夹角越小
如图所示,,两个平台水平距离为某同学先用一个小球从平台边缘以的速度水平抛出,结果小球落在了平台左侧下方处.取,忽略空气阻力.要使小球从平台边缘水平抛出能落到平台上,则从平台边缘水平抛出小球的速度至少为( )
A. B. C. D.
二、计算题(本大题共3小题,共40.0分)
如图所示,投壶是我国古代的一种投掷游戏,也是一种礼仪.据礼记投壶记载,以盛酒的壶口作为标的,在一定的距离内投箭矢,以投入多少决胜负,负者罚酒.儒家所奉行的“六艺”,即“礼、乐、射、御、书、数”,而投壶就来自于这六艺之一.现在有甲、乙两人进行投壶游戏,为简化起见,将箭矢视为质点球,并且不计空气阻力.如图所示,甲从离地面高的点以初速度水平抛出质点球,质点球正好落在壶口点,不计壶的高度.乙从离地面高的点水平抛出质点球,如果也要使质点球落到壶口点,则他抛球的初速度应该是多大?已知重力加速度
如图所示,水平屋顶高,墙高,墙到房子的距离,墙外马路宽,小球从房顶点水平飞出,取
若小球落在墙外的马路上,求小球在空中运动的时间;
若小球恰好经过墙顶点后落在马路上,求小球离开房顶时的速度;
若小球落在墙外的马路上,求小球离开房顶时的速度的取值范围。
如图所示,挡板与竖直方向所夹的锐角为,一小球视为质点从点正下方点以速度水平抛出,小球运动过程中恰好不和挡板碰撞小球轨迹所在平面与挡板垂直。不计空气阻力,重力加速度大小为,求
小球恰好不和挡板碰撞时的竖直速度大小。
、间的距离。
答案和解析
1.【答案】
【解析】解:根据得下落得时间为:,
从号位击球,当球恰好沿对角线落在界内时,速度最大,此时水平方向的位移为:
则击球的最大初速度为:。
所以:故A正确,BCD错误
故选:。
根据击球点与网的高度差求出球平抛运动的时间,结合击球点与网之间的水平距离求出球的最小初速度,根据击球点的高度求出平抛运动的时间,结合击球点与底线的水平距离求出球的最大初速度。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界情况,结合运动学公式灵活求解,难度不大。
2.【答案】
【解析】
【分析】
小物体做平抛运动,恰好擦着窗子上沿右侧穿过时最大。恰好擦着窗口下沿左侧时速度最小,由分位移公式求解。
解决本题的关键明确临界条件,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活解答。
【解答】
小物体做平抛运动,恰好擦着窗子上沿右侧穿过时最大。此时有 ,
代入解得:
恰好擦着窗口下沿左侧时速度最小,则有 ,
解得:
故的取值范围是,故ABC错误,D正确。
故选D。
3.【答案】
【解析】在点,据题可知小球的速度方向与水平方向成角,由速度的分解可知,竖直分速度大小为:
得:
故选:。
根据题意小球飞行过程中恰好与半圆轨道相切于点,可知速度的方向与水平方向成角,根据速度方向得到在点竖直分速度的大小,再根据平抛运动的规律和几何知识结合即可求解半圆柱体的半径。
解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,抓住速度方向,结合位移关系、速度关系进行求解。
4.【答案】
【解析】
【分析】
利用数学的几何关系可知,要到达蛛丝,那么蜘蛛到达蜘蛛网的速度恰好与水平方向成时初速度最小,再利用平抛运动的物理公式联立求解。
平抛运动和斜面的结合,而又不同于常规的考法,题目偏新颖,但解题方法依然是平抛运动和几何关系的综合应用,很好地让学生在模型迁移中得到成长。
【解答】
分析题意可知,蜘蛛到达蜘蛛网的时候速度与水平方向成时初速度最小,假设时间为,,,则,再根据几何关系知,根据平抛运动的规律知:,,
联立以上式子,解得,故ABD错误,C正确。
5.【答案】
【解析】
【分析】
若两名运动员都落地斜面上,则,得出水平位移之比;若两名运动员都落到水平地面上,根据可知,时间相等,再根据水平方向的运动分解水平位移之比。
本题是平抛运动和斜面相结合的问题,基础题目。
【解答】
设水平位移为,竖直位移为,两位运动员分别为、,若都落在斜面上,根据
即为
可得
根据
可得
当都落在水平面上时,由可知,运动时间相等,则,
综合上述可知,两名运动员水平位移之比最小为,故D不可能,故ABC均正确;
本题选择不可能的,故选D。
6.【答案】
【解析】
【分析】
平抛运动研究方法是分解成水平方向的匀速直线运动和竖直方向的自由落体运动两个分运动,两个分运动具有等时性,根据分运动公式即可求解。
本题考查平抛运动基本知识,需对平抛运动水平竖直两个方向得运动公式熟练掌握,解题时要注意取值范围和多解问题。
【解答】
根据,代入数据得:
由题意知水平位移最大为:,最小为:
根据代入数据得:,只有符合题意;
故选C。
7.【答案】
【解析】
【分析】
本题主要是考查了平抛运动的规律,知道平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;
解决本题的关键知道分运动和合运动具有等时性,知道平抛运动的时间由高度决定,与初速度、物体的质量等无关。
平抛运动的时间由高度决定;根据几何关系求解最大位移;位移大小与质量无关;
水平位移最大时初速度最大,根据平抛运动规律求解最大初速度。
【解答】
A.无论沿哪个方向平抛,运动时间都相同,根据可得在空中下落的时间为,故A错误;
B.从抛出点到右侧角时位移最大,故最大位移为,故B错误;
C.乒乓球从发射到落在台面上的位移大小与乒乓球的质量无关,故C错误;
D.乒乓球的最大水平位移为,乒乓球的最大初速度为,故D正确。
故选D。
8.【答案】
【解析】
【分析】
本题考查了平抛运动;解决本题的关键明确平抛运动的解决方法,掌握临界情况,速度最小时落在第三级台阶的边缘上,速度最大时落在第四级台阶边缘上。
小球以水平速度由第一级台阶上抛出欲打在第四级台阶上,求出两个临界情况,速度最小时打在第三级台阶的边缘上,速度最大时,打在第四级台阶的边缘上.根据和,得出的临界值。
【解答】
若小球打在第四级台阶的边缘上高度,根据,得;
水平位移则平抛的最大速度;
若小球打在第三级台阶的边缘上,高度,根据,得;
水平位移,则平抛运动的最小速度;
所以速度范围:;
故A正确,BCD错误。
故选A。
9.【答案】
【解析】
【分析】
根据平抛规律和推论逐一分析即可。
本题考查了平抛运动与斜面的结合,熟悉平抛运动规律是解题的关键。
【解答】
A.若石块恰能落到点,,则,,解得,,所以若,则石块可以落入水中,故A正确;
B.因为石块落水的时间均为,落到水中的竖直速度,由,可知石块能落入水中时,越大,落水时速度方向与水平面的夹角越小,故B错误;
C.若石块不能落入水中,则落到斜面上时位移方向与水平方向的夹角即位移偏转角恒为,由速度偏转角与位移偏转角关系满足,即速度偏转角为定值,落到斜面上时速度方向与斜面的夹角为定值,故CD错误。
故选A。
10.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度差求出即可。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,由运动学公式解答。
【解答】
由平抛运动的规律可知:;;
当小球恰能落到平台上时:;;
联立解得:;故B正确、ACD错误。
故选:。
11.【答案】解:设甲抛出的质点球做平抛运动的水平距离为,
则对甲抛出的质点球有 ,
联立解得
对乙抛出的质点球有 ,
联立解得.
【解析】同答案
12.【答案】解:根据得,小球在空中运动的时间.
设小球运动到墙顶点所用时间为
竖直方向上有:,
水平方向上有:
代入数据解得
最小时,小球恰好经过墙顶点后落在马路上,最大时,小球落在马路的最右端.
设的最大值为
竖直方向上有:
水平方向上有:
代入数据解得
所以小球抛出时的速度取值范围大小为 .
答:小球在空中运动的时间为;
小球离开房顶时的速度为;
小球离开房顶时的速度的取值范围为 .
【解析】根据高度出小球在空中运动的时间.
根据下降的高度求出平抛运动的时间,结合水平位移和时间求出小球离开房顶的速度.
抓住小球刚好经过墙顶以及小球刚好不落在马路上,结合两个临界状态,根据平抛运动的规律求出小球离开房顶的初速度取值范围.
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界状态,结合运动学公式灵活求解,难度不大.
13.【答案】解:由于小球恰好不和挡板碰撞,到达挡板时,速度方向与恰好平行,
则有:
解得:;
根据得,运动的时间为:
则小球做平抛运动的水平位移为:
竖直位移为:
设、间的距离为,由几何关系得:
联立解得:。
答:小球恰好不和挡板碰撞时的竖直速度大小为;
、间的距离为。
【解析】解决本题的关键是知道平抛运动在水平方向和竖直方向上的运动规律,明确小球恰好不和挡板碰撞的临界条件是速度方向与挡板平行,结合运动学公式和几何关系综合求解。
根据小球恰好不和挡板碰撞,达到挡板时,速度方向与挡板恰好平行,结合平行四边形定则求出竖直分速度的大小;
根据速度的关系求出平抛运动的时间,从而求出平抛运动的水平位移和竖直位移,结合几何关系求出间的距离。
第1页,共1页
