高中数学人教A版2019必修第二册 8.1.1 《棱柱、棱锥、棱台》导学案(含答案)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 8.1.1 《棱柱、棱锥、棱台》导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:36:51 | ||
图片预览


文档简介
棱柱、棱锥、棱台
1.通过对实物模型的观察,归纳认知简单多面体——棱柱、棱锥、棱台的结构特征.
2.能运用棱柱、棱锥、棱台的结构特征来判断、描述现实生活中的实物模型.
3.与平面几何体的有关概念、图形和性质进行适当类比,初步学会用类比的思想分析问题和解决问题.
1.数学抽象:多面体与旋转体等概念的理解;
2.逻辑推理:棱柱、棱锥、棱台的结构特点;
3.直观想象:判断空间几何体;
4.数学建模:通过平面展开图将空间问题转化为平面问题解决,体现了转化的思想方法.
重点:掌握棱柱、棱锥、棱台的结构特征;
难点:棱柱、棱锥和棱台的侧面展开图问题.
预习导入
阅读课本97-100页,填写。
1、空间几何体
定义:如果只考虑物体的_________和_________,而不考虑其它因素,那么这些由物体抽象出来的_________就叫做空间几何体。
2、多面体与旋转体
多面体的定义:由__________________围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的______;相邻两个面的__________叫做多面体的棱;棱与棱的__________叫做多面体的顶点.
旋转体的定义:由一个平面图形绕它所在的平面内的一条定_________旋转所形成的_________叫做旋转体.
3、、几种基本空间几何体的结构特征
(1)棱柱:有两个面互相_________,其余各面都是_________,并且每相邻两个四边形的公共边都互相_________。棱柱中,两个互相_________的面叫做棱柱的底面;其余各面叫做棱柱的侧面;相邻侧面的_________叫做棱柱的侧棱;侧面与底面的_________叫做棱柱的顶点。
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……
用各顶点_________表示棱柱,如棱柱ABCDEF-A’B’C’D’E’F’。
(2)棱锥:有一个面是_________,其余各面都是__________________的三角形.
底面是三角形、四边形、五边形……的棱锥分别叫做三棱锥、四棱锥、五棱锥……其中三棱锥又叫_________。
棱锥也用顶点和底面_________表示,如棱锥S-ABCD。
(3)棱台:用一个_________于棱锥底面的平面区截棱锥,_________之间的部分叫做棱台。
原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点。
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
用各_________表示棱柱,如棱台ABCDEF-A’B’C’D’E’F’。
1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)
(1)棱柱的侧面都是平行四边形.( )
(2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( )
(3)用一个平面去截棱锥,底面和截面之间的部分叫棱台.( )
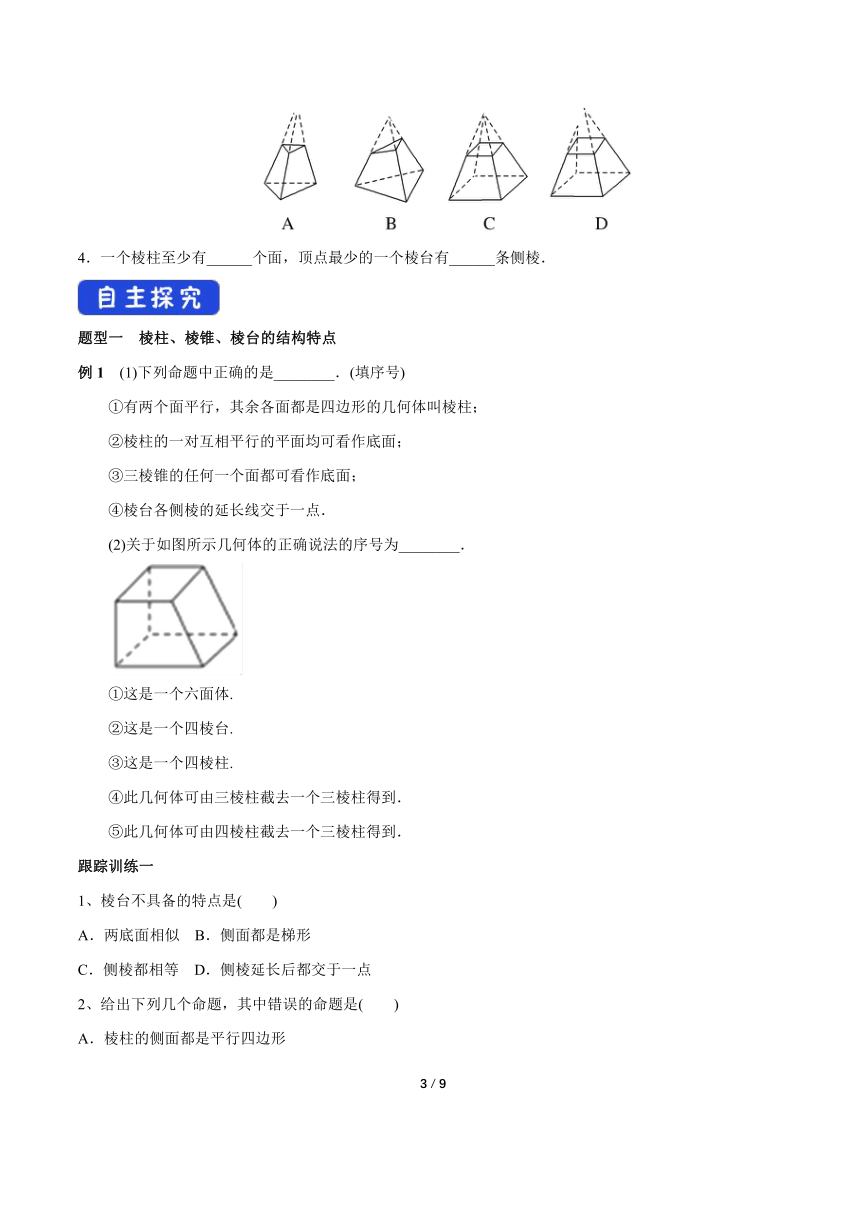
2.下面图形中,为棱锥的是( )
A.①③ B.①③④ C.①②④ D.①②
3.下列图形中,是棱台的是( )
4.一个棱柱至少有______个面,顶点最少的一个棱台有______条侧棱.
题型一 棱柱、棱锥、棱台的结构特点
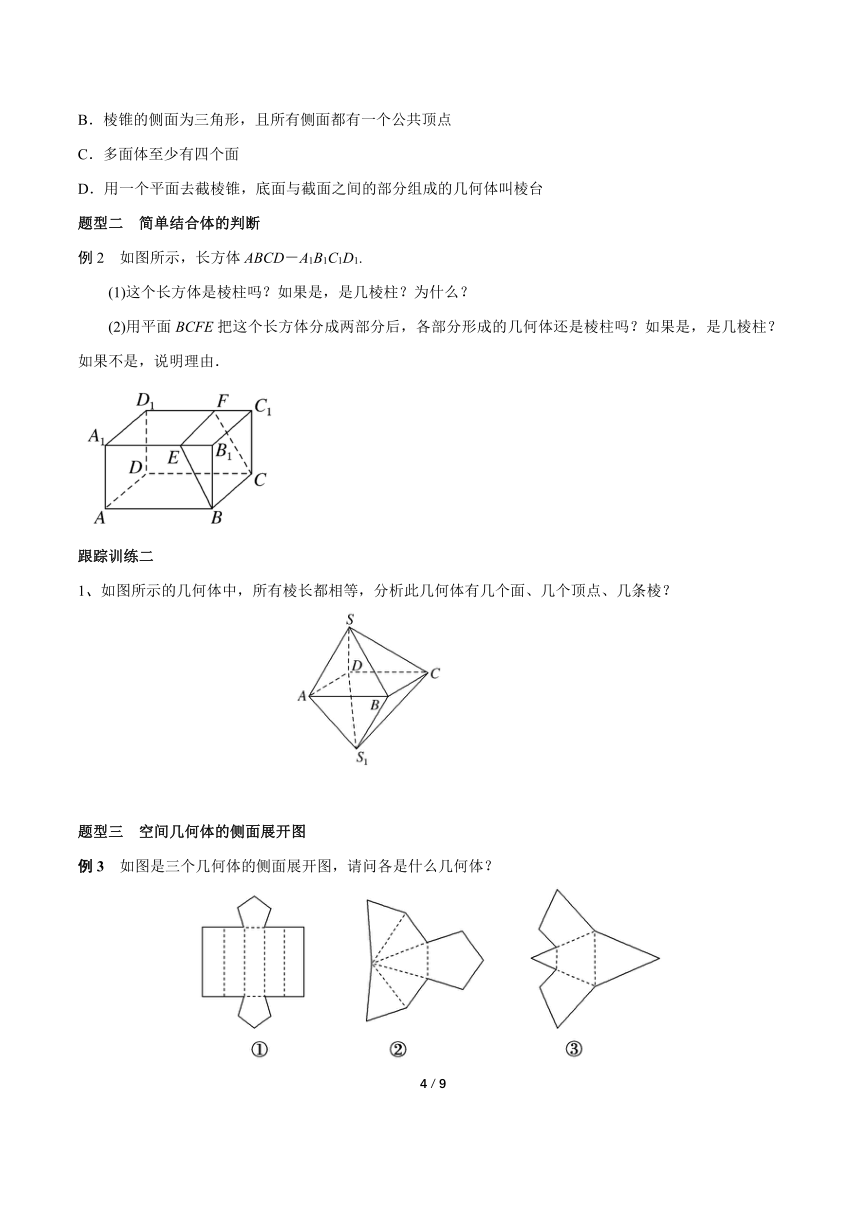
例1 (1)下列命题中正确的是________.(填序号)
①有两个面平行,其余各面都是四边形的几何体叫棱柱;
②棱柱的一对互相平行的平面均可看作底面;
③三棱锥的任何一个面都可看作底面;
④棱台各侧棱的延长线交于一点.
(2)关于如图所示几何体的正确说法的序号为________.
①这是一个六面体.
②这是一个四棱台.
③这是一个四棱柱.
④此几何体可由三棱柱截去一个三棱柱得到.
⑤此几何体可由四棱柱截去一个三棱柱得到.
跟踪训练一
1、棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
2、给出下列几个命题,其中错误的命题是( )
A.棱柱的侧面都是平行四边形
B.棱锥的侧面为三角形,且所有侧面都有一个公共顶点
C.多面体至少有四个面
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
题型二 简单结合体的判断
例2 如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,是几棱柱?如果不是,说明理由.
跟踪训练二
1、如图所示的几何体中,所有棱长都相等,分析此几何体有几个面、几个顶点、几条棱?
题型三 空间几何体的侧面展开图
例3 如图是三个几何体的侧面展开图,请问各是什么几何体?
例4 长方体ABCD-A1B1C1D1中,AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
跟踪训练三
1.下列四个平面图形中,每个小四边形都是正方形,其中可以沿相邻正方形的公共边折叠围成一个正方体的是( )
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图(图中数字写在正方体的外表面上),若图中“0”上方的“2”在正方体的上面,则这个正方体的下面是( )
A.1 B.2
C.快 D.乐
1.下面图形中,为棱锥的是( )
A.①③ B.①③④
C.①②④ D.①②
2.下列说法正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可能都是棱柱
3.一个棱台至少有________个面,面数最少的棱台有________个顶点,有________条棱.
4.一个无盖的正方体盒子的平面展开图如图所示,A,B,C是展开图上的三点,则在正方体盒子中,∠ABC=________.
5.如图所示是一个三棱台ABC-A′B′C′,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.
答案
小试牛刀
1. (1) √ (2)× (3)×
2.C.
3.C.
4. 5 3.
自主探究
例1 【答案】(1)③④ (2)①③④⑤.
【解析】(1)结合有关多面体的定义及性质判断.对于①,还可能是棱台;对于②,只要看一个正六棱柱模型即知是错的;对于③,显然是正确的;④显然符合定义.故填③④.
(2)①正确.因为有六个面,属于六面体的范围.②错误.因为侧棱的延长线不能交于一点,所以不正确.③正确.如果把几何体放倒就会发现是一个四棱柱.
④⑤都正确.如图所示.
跟踪训练一
【答案】1、C. 2、D.
【解析】1.由棱台的定义及特征知,A、B、D是棱台的特点,故选C.
2.根据各种几何体的概念与结构特征判断命题的真假.A、B均为真命题;对于C,一个图形要成为空间几何体,则它至少需有4个顶点,3个顶点只能构成平面图形,当有4个顶点时,可围成4个面,所以一个多面体至少应有4个面,而且这样的面必是三角形,故C也是真命题;对于D,只有当截面与底面平行时才对.
例2 【答案】(1)该长方体是棱柱,并且是四棱柱,祥见解析.
(2)截面BCFE上方部分是棱柱,且是三棱柱BEB1-CFC1,其中△BEB1和△CFC1是底面.
截面BCFE下方部分也是棱柱,且是四棱柱ABEA1-DCFD1,其中四边形ABEA1和DCFD1是底面.
【解析】(1)该长方体是棱柱,并且是四棱柱,因为以长方体相对的两个面作底面都是四边形,其余各面都是矩形,当然是平行四边形,并且四条侧棱互相平行.
(2)截面BCFE上方部分是棱柱,且是三棱柱BEB1-CFC1,其中△BEB1和△CFC1是底面.
截面BCFE下方部分也是棱柱,且是四棱柱ABEA1-DCFD1,其中四边形ABEA1和DCFD1是底面.
跟踪训练二
1、【答案】这个几何体有8个面;6个顶点;12条棱.
【解析】这个几何体有8个面,都是全等的正三角形;有6个顶点;有12条棱.
例3 【答案】 ①为五棱柱;②为五棱锥;③为三棱台.
【解析】 ①为五棱柱;②为五棱锥;③为三棱台.
例4 【答案】最短路线长为.
【解析】沿长方体的一条棱剪开,使A和C1展在同一平面上,求线段AC1的长即可,有如图所示的三种剪法:
(1)若将C1D1剪开,使面AB1与面A1C1共面,可求得AC1===4.
(2)若将AD剪开,使面AC与面BC1共面,可求得AC1===3.
(3)若将CC1剪开,使面BC1与面AB1共面,可求得AC1==.
相比较可得蚂蚁爬行的最短路线长为.
跟踪训练三
【答案】1、C.2、B.
【解析】1、选C 将四个选项中的平面图形折叠,看哪一个可以围成正方体.
2、选B 由题意,将正方体的展开图还原成正方体,1与乐相对,2与2相对,0与快相对,所以下面是2.
当堂检测
1-2. CD 3. 5 6 9. 4. 60°.
5.【答案】见解析
【解析】过A′,B,C三点作一个平面,再过A′,B,C′作一个平面,就把三棱台ABC-A′B′C′分成三部分,形成的三个三棱锥分别是A′-ABC,B-A′B′C′,A′-BCC′.(答案不唯一).
1 / 9
1.通过对实物模型的观察,归纳认知简单多面体——棱柱、棱锥、棱台的结构特征.
2.能运用棱柱、棱锥、棱台的结构特征来判断、描述现实生活中的实物模型.
3.与平面几何体的有关概念、图形和性质进行适当类比,初步学会用类比的思想分析问题和解决问题.
1.数学抽象:多面体与旋转体等概念的理解;
2.逻辑推理:棱柱、棱锥、棱台的结构特点;
3.直观想象:判断空间几何体;
4.数学建模:通过平面展开图将空间问题转化为平面问题解决,体现了转化的思想方法.
重点:掌握棱柱、棱锥、棱台的结构特征;
难点:棱柱、棱锥和棱台的侧面展开图问题.
预习导入
阅读课本97-100页,填写。
1、空间几何体
定义:如果只考虑物体的_________和_________,而不考虑其它因素,那么这些由物体抽象出来的_________就叫做空间几何体。
2、多面体与旋转体
多面体的定义:由__________________围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的______;相邻两个面的__________叫做多面体的棱;棱与棱的__________叫做多面体的顶点.
旋转体的定义:由一个平面图形绕它所在的平面内的一条定_________旋转所形成的_________叫做旋转体.
3、、几种基本空间几何体的结构特征
(1)棱柱:有两个面互相_________,其余各面都是_________,并且每相邻两个四边形的公共边都互相_________。棱柱中,两个互相_________的面叫做棱柱的底面;其余各面叫做棱柱的侧面;相邻侧面的_________叫做棱柱的侧棱;侧面与底面的_________叫做棱柱的顶点。
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……
用各顶点_________表示棱柱,如棱柱ABCDEF-A’B’C’D’E’F’。
(2)棱锥:有一个面是_________,其余各面都是__________________的三角形.
底面是三角形、四边形、五边形……的棱锥分别叫做三棱锥、四棱锥、五棱锥……其中三棱锥又叫_________。
棱锥也用顶点和底面_________表示,如棱锥S-ABCD。
(3)棱台:用一个_________于棱锥底面的平面区截棱锥,_________之间的部分叫做棱台。
原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点。
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
用各_________表示棱柱,如棱台ABCDEF-A’B’C’D’E’F’。
1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)
(1)棱柱的侧面都是平行四边形.( )
(2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( )
(3)用一个平面去截棱锥,底面和截面之间的部分叫棱台.( )
2.下面图形中,为棱锥的是( )
A.①③ B.①③④ C.①②④ D.①②
3.下列图形中,是棱台的是( )
4.一个棱柱至少有______个面,顶点最少的一个棱台有______条侧棱.
题型一 棱柱、棱锥、棱台的结构特点
例1 (1)下列命题中正确的是________.(填序号)
①有两个面平行,其余各面都是四边形的几何体叫棱柱;
②棱柱的一对互相平行的平面均可看作底面;
③三棱锥的任何一个面都可看作底面;
④棱台各侧棱的延长线交于一点.
(2)关于如图所示几何体的正确说法的序号为________.
①这是一个六面体.
②这是一个四棱台.
③这是一个四棱柱.
④此几何体可由三棱柱截去一个三棱柱得到.
⑤此几何体可由四棱柱截去一个三棱柱得到.
跟踪训练一
1、棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
2、给出下列几个命题,其中错误的命题是( )
A.棱柱的侧面都是平行四边形
B.棱锥的侧面为三角形,且所有侧面都有一个公共顶点
C.多面体至少有四个面
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
题型二 简单结合体的判断
例2 如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,是几棱柱?如果不是,说明理由.
跟踪训练二
1、如图所示的几何体中,所有棱长都相等,分析此几何体有几个面、几个顶点、几条棱?
题型三 空间几何体的侧面展开图
例3 如图是三个几何体的侧面展开图,请问各是什么几何体?
例4 长方体ABCD-A1B1C1D1中,AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
跟踪训练三
1.下列四个平面图形中,每个小四边形都是正方形,其中可以沿相邻正方形的公共边折叠围成一个正方体的是( )
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图(图中数字写在正方体的外表面上),若图中“0”上方的“2”在正方体的上面,则这个正方体的下面是( )
A.1 B.2
C.快 D.乐
1.下面图形中,为棱锥的是( )
A.①③ B.①③④
C.①②④ D.①②
2.下列说法正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可能都是棱柱
3.一个棱台至少有________个面,面数最少的棱台有________个顶点,有________条棱.
4.一个无盖的正方体盒子的平面展开图如图所示,A,B,C是展开图上的三点,则在正方体盒子中,∠ABC=________.
5.如图所示是一个三棱台ABC-A′B′C′,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.
答案
小试牛刀
1. (1) √ (2)× (3)×
2.C.
3.C.
4. 5 3.
自主探究
例1 【答案】(1)③④ (2)①③④⑤.
【解析】(1)结合有关多面体的定义及性质判断.对于①,还可能是棱台;对于②,只要看一个正六棱柱模型即知是错的;对于③,显然是正确的;④显然符合定义.故填③④.
(2)①正确.因为有六个面,属于六面体的范围.②错误.因为侧棱的延长线不能交于一点,所以不正确.③正确.如果把几何体放倒就会发现是一个四棱柱.
④⑤都正确.如图所示.
跟踪训练一
【答案】1、C. 2、D.
【解析】1.由棱台的定义及特征知,A、B、D是棱台的特点,故选C.
2.根据各种几何体的概念与结构特征判断命题的真假.A、B均为真命题;对于C,一个图形要成为空间几何体,则它至少需有4个顶点,3个顶点只能构成平面图形,当有4个顶点时,可围成4个面,所以一个多面体至少应有4个面,而且这样的面必是三角形,故C也是真命题;对于D,只有当截面与底面平行时才对.
例2 【答案】(1)该长方体是棱柱,并且是四棱柱,祥见解析.
(2)截面BCFE上方部分是棱柱,且是三棱柱BEB1-CFC1,其中△BEB1和△CFC1是底面.
截面BCFE下方部分也是棱柱,且是四棱柱ABEA1-DCFD1,其中四边形ABEA1和DCFD1是底面.
【解析】(1)该长方体是棱柱,并且是四棱柱,因为以长方体相对的两个面作底面都是四边形,其余各面都是矩形,当然是平行四边形,并且四条侧棱互相平行.
(2)截面BCFE上方部分是棱柱,且是三棱柱BEB1-CFC1,其中△BEB1和△CFC1是底面.
截面BCFE下方部分也是棱柱,且是四棱柱ABEA1-DCFD1,其中四边形ABEA1和DCFD1是底面.
跟踪训练二
1、【答案】这个几何体有8个面;6个顶点;12条棱.
【解析】这个几何体有8个面,都是全等的正三角形;有6个顶点;有12条棱.
例3 【答案】 ①为五棱柱;②为五棱锥;③为三棱台.
【解析】 ①为五棱柱;②为五棱锥;③为三棱台.
例4 【答案】最短路线长为.
【解析】沿长方体的一条棱剪开,使A和C1展在同一平面上,求线段AC1的长即可,有如图所示的三种剪法:
(1)若将C1D1剪开,使面AB1与面A1C1共面,可求得AC1===4.
(2)若将AD剪开,使面AC与面BC1共面,可求得AC1===3.
(3)若将CC1剪开,使面BC1与面AB1共面,可求得AC1==.
相比较可得蚂蚁爬行的最短路线长为.
跟踪训练三
【答案】1、C.2、B.
【解析】1、选C 将四个选项中的平面图形折叠,看哪一个可以围成正方体.
2、选B 由题意,将正方体的展开图还原成正方体,1与乐相对,2与2相对,0与快相对,所以下面是2.
当堂检测
1-2. CD 3. 5 6 9. 4. 60°.
5.【答案】见解析
【解析】过A′,B,C三点作一个平面,再过A′,B,C′作一个平面,就把三棱台ABC-A′B′C′分成三部分,形成的三个三棱锥分别是A′-ABC,B-A′B′C′,A′-BCC′.(答案不唯一).
1 / 9
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
