高中数学人教A版2019必修第二册 8.1.1《棱柱、棱锥、棱台》教学设计(表格式)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 8.1.1《棱柱、棱锥、棱台》教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:37:24 | ||
图片预览



文档简介
棱柱、棱锥、棱台
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课是第1课时,本节课主要学习棱柱、棱锥、棱台的概念及结构特征。
教材首先让学生观察现实世界中实物的图片,引导学生将观察到的实物进行归纳、分类抽象、概括,得出柱体、锥体、台体的结构特征,在此基础上给出由它们组合而成的简单几何体的结构特征.
空间几何体是新课程立体几何部分的起始课程,它在土木建筑、机械设计、航海测绘等大量实际问题中都有广泛的应用,新课程从对空间几何体的整体观察入手,再研究组成空间几何体的点、直线和平面.这种安排降低了立体几何学习入门难的门槛,强调几何直观,淡化几何论证,可以激发学生学习立体几何的兴趣。
课程目标 学科素养
A.能根据几何结构特征对空间物体进行分类; B.从实物中概括出棱柱、棱锥、棱台的几何结构特征; C.会用语言概述棱柱、棱锥、棱台的结构特征; D.会表示有关几何体以及棱柱、棱锥、棱台的分类。 1.数学抽象:棱柱、棱锥、棱台的几何结构特征; 2.逻辑推理:从实物中概括出棱柱、棱锥、棱台的几何结构特征; 3..直观想象:棱柱、棱锥、棱台的分类;
1.教学重点:让学生感受大量空间实物及模型、概括出棱柱、棱锥、棱台的结构特征;
2.教学难点:棱柱、棱锥、棱台的结构特征的概括。
多媒体
教学过程 教学设计意图 核心素养目标
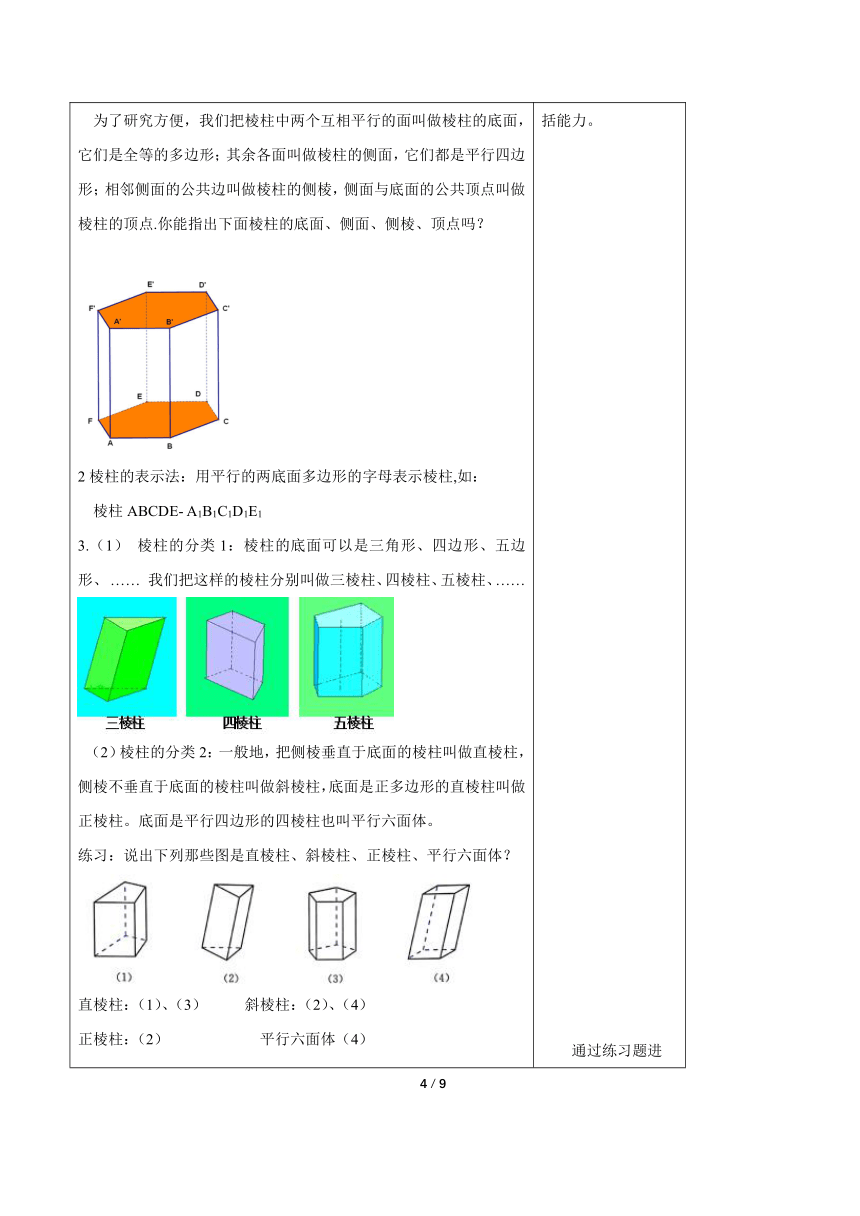
复习回顾,温故知新 1.通过生活中的图片引入,初步感受空间几何体。 二、探索新知 观察1:观察生活的具体实物,你能抽象出它们的空间图形吗? 空间几何体的定义: 如果我们只考虑这些物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体. 思考1:如图,下面这些图片中的物体具有怎样的形状?在日常生活中,我们把这些物体的形状叫做什么?如何描述它们的形状? 【答案】纸箱、金字塔、茶叶盒、水晶萤石、储物箱等物体围成它们的面都是平面图形,并且都是平面多边形;纸杯、腰鼓、奶粉罐、篮球和足球、铅锤围成它们的面不全是平面图形,有些面是曲面。 1.多面体:由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。 面ABE,面BAF,棱AE,棱EC,顶点E,顶点C 2.旋转体:由一条平面曲线(包括直线)绕它所在的平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴。 思考2:观察下面的长方体,它的每个面是什么样多边形?不同的面之间有什么位置关系? 【答案】它的每个面是平行四边形,不同的面之间位置关系有平行、相交,相对面平行。 (一)棱柱 1.棱柱定义: 一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱. 为了研究方便,我们把棱柱中两个互相平行的面叫做棱柱的底面,它们是全等的多边形;其余各面叫做棱柱的侧面,它们都是平行四边形;相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.你能指出下面棱柱的底面、侧面、侧棱、顶点吗? 2棱柱的表示法:用平行的两底面多边形的字母表示棱柱,如: 棱柱ABCDE- A1B1C1D1E1 3.(1) 棱柱的分类1:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… (2)棱柱的分类2:一般地,把侧棱垂直于底面的棱柱叫做直棱柱,侧棱不垂直于底面的棱柱叫做斜棱柱,底面是正多边形的直棱柱叫做正棱柱。底面是平行四边形的四棱柱也叫平行六面体。 练习:说出下列那些图是直棱柱、斜棱柱、正棱柱、平行六面体? 直棱柱:(1)、(3) 斜棱柱:(2)、(4) 正棱柱:(2) 平行六面体(4) 4.棱柱的性质: (1)侧棱都互相平行且相等,各侧面都是平行四边形;直棱柱的每条侧棱及每个侧面都垂直于底面。 (2)两个底面及平行于底面的截面是全等的多边形,且对应边互相平行; (3)过不相邻的两条侧棱的截面(即对角面)是平行四边形; 练习:下列命题中正确的是( ) A、有两个面平行,其余各面都是四边形的几何体叫棱柱。 B、有两个面平行,其余各面都是平行四边形的几何体叫棱柱。 C、有两个侧面是矩形的棱柱是直棱柱。 D、有两个相邻侧面垂直与底面的棱柱是直棱柱。 【答案】D (二)棱锥 思考3:上图中的物体具有什么样的共同的结构特征? 【答案】一个面是多边形,其余各面是有 一个公共顶点的三角形。 1.棱锥的定义: 有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥。这个多边形面叫做棱锥的底面;有公共顶点的各个三角形面叫做棱锥的侧面;相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点。 2.棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。 3.棱锥的分类: 按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……其中三棱锥又叫四面体,底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。 练习:下面几何体是棱锥吗? 【答案】不是,各侧面没有公共点。 (三)棱台 1.棱台的概念: 用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分多面体叫做棱台。原棱锥的底面和截面分别叫做棱台的下底面和上底面。 思考4:请你仿照棱锥中侧面、侧棱、顶点的定义,给出棱台侧面、侧棱、顶点的定义,并在棱台中标出。 2.棱台的表示法:棱台用表示上、下底面各顶点的字母来表示:如 棱台ABCDE-A1B1C1D1E1。 3.棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台… 练习:判断:下列几何体是不是棱台,为什么 【答案】(1)不是,侧棱不交于一点; (2)不是,没有两面平行; 思考5.棱台的结构特征是什么? 【答案】①各侧棱的延长线相交于一点; ②截面平行于原棱锥的底面。 例1.将下列各类几何体之间的关系用Venn图表示出来:多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体 解:如图所示 通过观察图片,引入本节新课。激发学生的学习兴趣。 通过思考,观察几何体的形状、不同,得到多面体、旋转体的定义,提高学生分析问题的能力、概括能力。 通过思考,思考长方体的特点,概括出棱柱的定义,提高学生分析问题的能力、概括能力。 通过练习题进一步巩固棱柱的分类,提高学生解决问题的能力。 通过练习题进一步巩固棱柱的定义,提高学生解决问题的能力。 通过思考,观察图形的特征,概括出棱锥的定义,提高学生分析问题的能力、概括能力。 通过练习,进一步巩固棱锥的定义,通过学生应用所学知识解决问题的能力。 通过练习,进一步巩固棱台的定义,通过学生应用所学知识解决问题的能力。 通过例题的讲解,让学生进一步理解多面体的分类,提高学生解决与分析问题的能力。
三、达标检测 1.判断正误 (1)棱柱的侧面都是平行四边形.( ) (2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( ) (3)用一平面去截棱锥底面和截面之间的部分叫棱台.( ) 【答案】 (1)√ (2)× (3)× 2.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( ) A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥 【答案】D 【解析】根据棱锥的定义可知该几何体是三棱锥.故选D。 3.下列图形经过折叠可以围成一个棱柱的是( ) A B C D 【答案】D 【解析】A,B,C中底面多边形的边数与侧面数不相等.故选D。 4.一个棱柱至少有 个面,顶点最少的一个棱台有 条侧棱. 【答案】5 3 【解析】面最少的棱柱是三棱柱,它有5个面;顶点最少的一个棱台是三棱台,它有3条侧棱. 5.画一个三棱台,再把它分成: (1)一个三棱柱和另一个多面体; (2)三个三棱锥,并用字母表示. 【解析】 画三棱台一定要利用三棱锥. (1)如图①所示,三棱柱是棱柱A′B′C′ AB″C″,另一个多面体是B′C′CBB″C″. (2)如图②所示,三个三棱锥分别是A′ ABC, B′ A′BC,C′ A′B′C. 通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结 一、多面体及旋转体的定义 二、棱柱的结构特征: (1)底面互相平行. (2)侧面都是平行四边形. (3)侧棱平行且相等 三、棱锥的结构特征:一个面是多边形,其余各面是有一个公共顶点的三角形。 四、棱台的结构特征: ①各侧棱的延长线相交于一点; ②截面平行于原棱锥的底面。 五、作业 习题3.1 6,7,9题 通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
通过本节授课有一些心得。如在引导学生进行归纳总结的时候,教师应该不着急于给出正确的答案。学生初始的回答可能只是其中的一两点,而且不完整,甚至有错误的见解。教师应该对于正确的及时给予肯定和鼓励。通过教师的鼓励,能大幅度地调动其他学生的积极性和增加其他学生回答问题的勇气。这样其他学生就能自主地给予修正补充。充分发挥协作学习,达到事半功倍的效果。
1 / 9
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课是第1课时,本节课主要学习棱柱、棱锥、棱台的概念及结构特征。
教材首先让学生观察现实世界中实物的图片,引导学生将观察到的实物进行归纳、分类抽象、概括,得出柱体、锥体、台体的结构特征,在此基础上给出由它们组合而成的简单几何体的结构特征.
空间几何体是新课程立体几何部分的起始课程,它在土木建筑、机械设计、航海测绘等大量实际问题中都有广泛的应用,新课程从对空间几何体的整体观察入手,再研究组成空间几何体的点、直线和平面.这种安排降低了立体几何学习入门难的门槛,强调几何直观,淡化几何论证,可以激发学生学习立体几何的兴趣。
课程目标 学科素养
A.能根据几何结构特征对空间物体进行分类; B.从实物中概括出棱柱、棱锥、棱台的几何结构特征; C.会用语言概述棱柱、棱锥、棱台的结构特征; D.会表示有关几何体以及棱柱、棱锥、棱台的分类。 1.数学抽象:棱柱、棱锥、棱台的几何结构特征; 2.逻辑推理:从实物中概括出棱柱、棱锥、棱台的几何结构特征; 3..直观想象:棱柱、棱锥、棱台的分类;
1.教学重点:让学生感受大量空间实物及模型、概括出棱柱、棱锥、棱台的结构特征;
2.教学难点:棱柱、棱锥、棱台的结构特征的概括。
多媒体
教学过程 教学设计意图 核心素养目标
复习回顾,温故知新 1.通过生活中的图片引入,初步感受空间几何体。 二、探索新知 观察1:观察生活的具体实物,你能抽象出它们的空间图形吗? 空间几何体的定义: 如果我们只考虑这些物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体. 思考1:如图,下面这些图片中的物体具有怎样的形状?在日常生活中,我们把这些物体的形状叫做什么?如何描述它们的形状? 【答案】纸箱、金字塔、茶叶盒、水晶萤石、储物箱等物体围成它们的面都是平面图形,并且都是平面多边形;纸杯、腰鼓、奶粉罐、篮球和足球、铅锤围成它们的面不全是平面图形,有些面是曲面。 1.多面体:由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。 面ABE,面BAF,棱AE,棱EC,顶点E,顶点C 2.旋转体:由一条平面曲线(包括直线)绕它所在的平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴。 思考2:观察下面的长方体,它的每个面是什么样多边形?不同的面之间有什么位置关系? 【答案】它的每个面是平行四边形,不同的面之间位置关系有平行、相交,相对面平行。 (一)棱柱 1.棱柱定义: 一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱. 为了研究方便,我们把棱柱中两个互相平行的面叫做棱柱的底面,它们是全等的多边形;其余各面叫做棱柱的侧面,它们都是平行四边形;相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.你能指出下面棱柱的底面、侧面、侧棱、顶点吗? 2棱柱的表示法:用平行的两底面多边形的字母表示棱柱,如: 棱柱ABCDE- A1B1C1D1E1 3.(1) 棱柱的分类1:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… (2)棱柱的分类2:一般地,把侧棱垂直于底面的棱柱叫做直棱柱,侧棱不垂直于底面的棱柱叫做斜棱柱,底面是正多边形的直棱柱叫做正棱柱。底面是平行四边形的四棱柱也叫平行六面体。 练习:说出下列那些图是直棱柱、斜棱柱、正棱柱、平行六面体? 直棱柱:(1)、(3) 斜棱柱:(2)、(4) 正棱柱:(2) 平行六面体(4) 4.棱柱的性质: (1)侧棱都互相平行且相等,各侧面都是平行四边形;直棱柱的每条侧棱及每个侧面都垂直于底面。 (2)两个底面及平行于底面的截面是全等的多边形,且对应边互相平行; (3)过不相邻的两条侧棱的截面(即对角面)是平行四边形; 练习:下列命题中正确的是( ) A、有两个面平行,其余各面都是四边形的几何体叫棱柱。 B、有两个面平行,其余各面都是平行四边形的几何体叫棱柱。 C、有两个侧面是矩形的棱柱是直棱柱。 D、有两个相邻侧面垂直与底面的棱柱是直棱柱。 【答案】D (二)棱锥 思考3:上图中的物体具有什么样的共同的结构特征? 【答案】一个面是多边形,其余各面是有 一个公共顶点的三角形。 1.棱锥的定义: 有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥。这个多边形面叫做棱锥的底面;有公共顶点的各个三角形面叫做棱锥的侧面;相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点。 2.棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。 3.棱锥的分类: 按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……其中三棱锥又叫四面体,底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。 练习:下面几何体是棱锥吗? 【答案】不是,各侧面没有公共点。 (三)棱台 1.棱台的概念: 用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分多面体叫做棱台。原棱锥的底面和截面分别叫做棱台的下底面和上底面。 思考4:请你仿照棱锥中侧面、侧棱、顶点的定义,给出棱台侧面、侧棱、顶点的定义,并在棱台中标出。 2.棱台的表示法:棱台用表示上、下底面各顶点的字母来表示:如 棱台ABCDE-A1B1C1D1E1。 3.棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台… 练习:判断:下列几何体是不是棱台,为什么 【答案】(1)不是,侧棱不交于一点; (2)不是,没有两面平行; 思考5.棱台的结构特征是什么? 【答案】①各侧棱的延长线相交于一点; ②截面平行于原棱锥的底面。 例1.将下列各类几何体之间的关系用Venn图表示出来:多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体 解:如图所示 通过观察图片,引入本节新课。激发学生的学习兴趣。 通过思考,观察几何体的形状、不同,得到多面体、旋转体的定义,提高学生分析问题的能力、概括能力。 通过思考,思考长方体的特点,概括出棱柱的定义,提高学生分析问题的能力、概括能力。 通过练习题进一步巩固棱柱的分类,提高学生解决问题的能力。 通过练习题进一步巩固棱柱的定义,提高学生解决问题的能力。 通过思考,观察图形的特征,概括出棱锥的定义,提高学生分析问题的能力、概括能力。 通过练习,进一步巩固棱锥的定义,通过学生应用所学知识解决问题的能力。 通过练习,进一步巩固棱台的定义,通过学生应用所学知识解决问题的能力。 通过例题的讲解,让学生进一步理解多面体的分类,提高学生解决与分析问题的能力。
三、达标检测 1.判断正误 (1)棱柱的侧面都是平行四边形.( ) (2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( ) (3)用一平面去截棱锥底面和截面之间的部分叫棱台.( ) 【答案】 (1)√ (2)× (3)× 2.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( ) A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥 【答案】D 【解析】根据棱锥的定义可知该几何体是三棱锥.故选D。 3.下列图形经过折叠可以围成一个棱柱的是( ) A B C D 【答案】D 【解析】A,B,C中底面多边形的边数与侧面数不相等.故选D。 4.一个棱柱至少有 个面,顶点最少的一个棱台有 条侧棱. 【答案】5 3 【解析】面最少的棱柱是三棱柱,它有5个面;顶点最少的一个棱台是三棱台,它有3条侧棱. 5.画一个三棱台,再把它分成: (1)一个三棱柱和另一个多面体; (2)三个三棱锥,并用字母表示. 【解析】 画三棱台一定要利用三棱锥. (1)如图①所示,三棱柱是棱柱A′B′C′ AB″C″,另一个多面体是B′C′CBB″C″. (2)如图②所示,三个三棱锥分别是A′ ABC, B′ A′BC,C′ A′B′C. 通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结 一、多面体及旋转体的定义 二、棱柱的结构特征: (1)底面互相平行. (2)侧面都是平行四边形. (3)侧棱平行且相等 三、棱锥的结构特征:一个面是多边形,其余各面是有一个公共顶点的三角形。 四、棱台的结构特征: ①各侧棱的延长线相交于一点; ②截面平行于原棱锥的底面。 五、作业 习题3.1 6,7,9题 通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
通过本节授课有一些心得。如在引导学生进行归纳总结的时候,教师应该不着急于给出正确的答案。学生初始的回答可能只是其中的一两点,而且不完整,甚至有错误的见解。教师应该对于正确的及时给予肯定和鼓励。通过教师的鼓励,能大幅度地调动其他学生的积极性和增加其他学生回答问题的勇气。这样其他学生就能自主地给予修正补充。充分发挥协作学习,达到事半功倍的效果。
1 / 9
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
