人教A版(2019)数学必修第一册4.2.2指数函数图象及其性质应用 课件(共张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册4.2.2指数函数图象及其性质应用 课件(共张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 792.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:44:32 | ||
图片预览











文档简介
(共34张PPT)
4.2 指数函数图象及其性质的应用
高一
必修一
本节目标
1.掌握指数函数的图象和性质.
2.掌握函数图象的平移变换和对称变换.
3.会解指数函数型的应用题.
任务一:知识预习
课前预习
(1) 指数函数具有哪些性质?
(2) 解决指数函数应用题的步骤有哪些?
预习课本P117~120,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
2.指数函数y=ax与y=bx的图象如图,则( )
A.a<0,b<0
B.a<0,b>0
C.01
D.0C
任务二:简单题型通关
课前预习
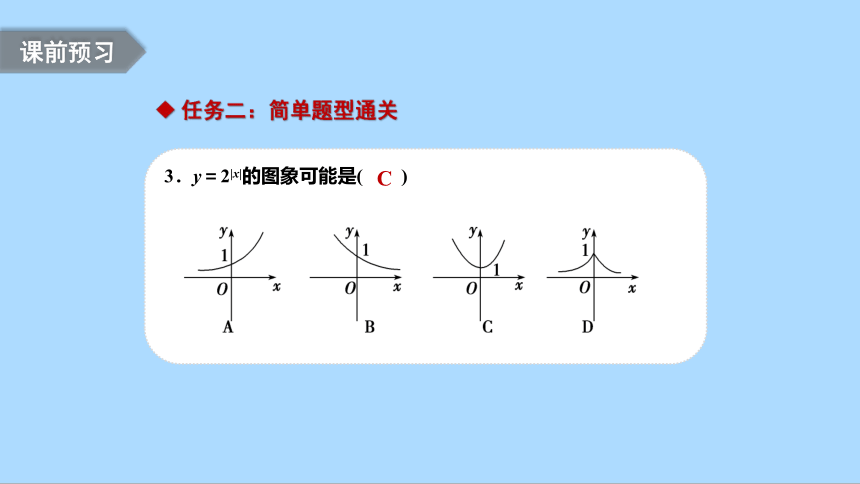
3.y=2|x|的图象可能是( )
C
任务二:简单题型通关
课前预习
(0,2)
新知精讲
若已知y=ax的图象,则
把y=ax的图象向左平移b(b>0)个单位,得到 y=ax+b的图象;
把y=ax的图象向右平移b(b>0)个单位,得到 y=ax-b的图象;
把y=ax的图象向上平移b(b>0)个单位,得到 y=ax+b的图象;
把y=ax的图象向下平移b(b>0)个单位,得到 y=ax-b的图象.
1、图象平移
新知精讲
2、图象对称
若已知y=ax的图象, 则y=ax在y轴右侧的图象不变,并把y=ax在y轴右侧的图象关于y轴对称翻折,即得y=a|x|图象.
新知精讲
3、指数型函数模型
题型探究
题型一 指数函数的图象
[例1] 如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a,b,c,d与1的大小关系为( )
A.a<b<1<c<d
B.b<a<1<d<c
C.1<a<b<c<d
D.a<b<1<d<c
B
归纳总结
指数函数的图象随底数变化的规律
(1)无论指数函数的底数a如何变化,指数函数y=ax的图象与直线x=1相交于点(1,a),由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
(2)指数函数的底数与图象间的关系可概括记忆为:在第一象限内,底数自下而上依次增大.
活学活用
B
题型探究
题型二
函数图象的变换
[例2] 利用函数f(x)=2x的图象,作出下列各函数的图象.
(1)f(x-1); (2)f(x+1); (3)-f(x); (4)f(-x); (5)f(x)-1; (6)f(|x|).
归纳总结
利用熟悉的函数图象作图,主要利用图象的平移、对称等变换,
平移需分清楚向何方向平移,要移几个单位;
对称需分清楚对称轴是什么,可以通过点与点的坐标关系来判断等.
活学活用
2. (1) f(x)=ax-1+1过定点________.
(2)函数y=a2x+b+1(a>0且a≠1,b∈R)的图象恒过定点(1,2),则b的值为________.
(3) y=a|x|的图象关于________对称( )
A.x轴 B.y轴
C.原点 D.y=x
(1,2)
-2
B
题型探究
题型三
指数函数的性质
题型探究
1
题型探究
f(1)+f(-1)=0
a=
题型探究
﹣2
归纳总结
以指数型函数为背景来考查函数的奇偶性,可以用
(1)定义法;(2)图象法;(3)特殊值法来处理.
活学活用
B
题型探究
题型探究
归纳总结
求y=af(x)单调区间的步骤
(1)确定f(x)的定义域D.
(2)若a>1,要求原函数的增区间,只需求定义域D内f(x)的增区间;
要求原函数的减区间,只需求定义域D内f(x)的减区间.
若0要求原函数的减区间,只需求定义域D内f(x)的增区间.
活学活用
题型探究
题型四
指数函数的实际应用
[例5] 某林区2017年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并写出此函数的定义域.
题型探究
[例5] 某林区2017年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并写出此函数的定义域.
归纳总结
解决指数函数应用题的流程
(1)审题:理解题意,弄清楚关键字词和字母的意义,从题意中提取信息.
(2)建模:据已知条件,列出指数函数的关系式.
(3)解模:运用数学知识解决问题.
(4)回归:还原为实际问题,归纳得出结论.
活学活用
5.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
19
假设第一天荷叶覆盖水面面积为1,
则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,
当x=20时,长满水面,
所以生长19天时,荷叶布满水面一半.
达标检测
A
达标检测
f(x)是定义在R上的奇函数
达标检测
本课小结
1、 指数函数具有哪些性质?
2、 解决指数函数应用题的步骤有哪些?
3、图象平移变换、对称变换有哪些规律?
4.2 指数函数图象及其性质的应用
高一
必修一
本节目标
1.掌握指数函数的图象和性质.
2.掌握函数图象的平移变换和对称变换.
3.会解指数函数型的应用题.
任务一:知识预习
课前预习
(1) 指数函数具有哪些性质?
(2) 解决指数函数应用题的步骤有哪些?
预习课本P117~120,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
2.指数函数y=ax与y=bx的图象如图,则( )
A.a<0,b<0
B.a<0,b>0
C.0
D.0
任务二:简单题型通关
课前预习
3.y=2|x|的图象可能是( )
C
任务二:简单题型通关
课前预习
(0,2)
新知精讲
若已知y=ax的图象,则
把y=ax的图象向左平移b(b>0)个单位,得到 y=ax+b的图象;
把y=ax的图象向右平移b(b>0)个单位,得到 y=ax-b的图象;
把y=ax的图象向上平移b(b>0)个单位,得到 y=ax+b的图象;
把y=ax的图象向下平移b(b>0)个单位,得到 y=ax-b的图象.
1、图象平移
新知精讲
2、图象对称
若已知y=ax的图象, 则y=ax在y轴右侧的图象不变,并把y=ax在y轴右侧的图象关于y轴对称翻折,即得y=a|x|图象.
新知精讲
3、指数型函数模型
题型探究
题型一 指数函数的图象
[例1] 如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a,b,c,d与1的大小关系为( )
A.a<b<1<c<d
B.b<a<1<d<c
C.1<a<b<c<d
D.a<b<1<d<c
B
归纳总结
指数函数的图象随底数变化的规律
(1)无论指数函数的底数a如何变化,指数函数y=ax的图象与直线x=1相交于点(1,a),由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
(2)指数函数的底数与图象间的关系可概括记忆为:在第一象限内,底数自下而上依次增大.
活学活用
B
题型探究
题型二
函数图象的变换
[例2] 利用函数f(x)=2x的图象,作出下列各函数的图象.
(1)f(x-1); (2)f(x+1); (3)-f(x); (4)f(-x); (5)f(x)-1; (6)f(|x|).
归纳总结
利用熟悉的函数图象作图,主要利用图象的平移、对称等变换,
平移需分清楚向何方向平移,要移几个单位;
对称需分清楚对称轴是什么,可以通过点与点的坐标关系来判断等.
活学活用
2. (1) f(x)=ax-1+1过定点________.
(2)函数y=a2x+b+1(a>0且a≠1,b∈R)的图象恒过定点(1,2),则b的值为________.
(3) y=a|x|的图象关于________对称( )
A.x轴 B.y轴
C.原点 D.y=x
(1,2)
-2
B
题型探究
题型三
指数函数的性质
题型探究
1
题型探究
f(1)+f(-1)=0
a=
题型探究
﹣2
归纳总结
以指数型函数为背景来考查函数的奇偶性,可以用
(1)定义法;(2)图象法;(3)特殊值法来处理.
活学活用
B
题型探究
题型探究
归纳总结
求y=af(x)单调区间的步骤
(1)确定f(x)的定义域D.
(2)若a>1,要求原函数的增区间,只需求定义域D内f(x)的增区间;
要求原函数的减区间,只需求定义域D内f(x)的减区间.
若0
活学活用
题型探究
题型四
指数函数的实际应用
[例5] 某林区2017年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并写出此函数的定义域.
题型探究
[例5] 某林区2017年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均增长率能达到5%.若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并写出此函数的定义域.
归纳总结
解决指数函数应用题的流程
(1)审题:理解题意,弄清楚关键字词和字母的意义,从题意中提取信息.
(2)建模:据已知条件,列出指数函数的关系式.
(3)解模:运用数学知识解决问题.
(4)回归:还原为实际问题,归纳得出结论.
活学活用
5.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
19
假设第一天荷叶覆盖水面面积为1,
则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,
当x=20时,长满水面,
所以生长19天时,荷叶布满水面一半.
达标检测
A
达标检测
f(x)是定义在R上的奇函数
达标检测
本课小结
1、 指数函数具有哪些性质?
2、 解决指数函数应用题的步骤有哪些?
3、图象平移变换、对称变换有哪些规律?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
