人教A版(2019)数学必修第一册4.2.1指数函数图象及其性质 课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册4.2.1指数函数图象及其性质 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:45:16 | ||
图片预览











文档简介
(共34张PPT)
4.2 指数函数图象及其性质
高一
必修一
情景引入
某公名曰白日梦,某日向某公司老板求职,老板答应他:试用一周(7天),日工资20元。白日梦对老板说:“日工资是否能再谈一谈?”老板很随和地说:“你开个价吧!”白日梦心中暗喜,说道:“第一天您须付给我5分钱,以后每天付给的工资,第几天就是几个第一天工资相乘。”老板一听,略作思考后答应了,并叫来秘书与白日梦签订如下合同:“经双方同意,白日梦在试用期间的工资按如下方案付给:第一天付给0.05元,以后每天付给的工资,第几天就是几个第一天工资相乘。”
情景引入
签完合同后,白日梦高兴得手舞足蹈,躺在床上沾沾自喜地盘算着:第一天付给我5分,第二天付给我52=25(分),第三天付给我53=125(分),第四天付给我54=625(分)。虽然先吃了亏,可是到了第五天便可拿55=3125(分)=31.25(元);第六天就更多了,可达56分=156.25(元);第七天就更不得了,竟有57分=781.25(元)。这样一来,一星期可捞到976.55元。
次日,白日梦干起活来特别卖力,老板看在眼里,喜在心里。7天一到,秘书根据合同一算,只付给他6分钱,还说多给了半分多。白日梦一下子傻了,他搞不清楚5分与0.05元到底有何区别?!本想大挣一笔,没想到白干了7天。
情景引入
秘书的计算是:
第二天0.052=0.0025(元),第三天0.053=0.000125(元),第四天0.054=0.00000625(元),……,第七天0.057=0.00000000078125(元)。
七天共应付给:0.05+0.0025+0.000125+0.00000625+0.0000003125+0.000000015625+0.00000000078125≈
0.0526(元)。
现在如果有人问你:5分等于0.05元吗?你不得不对这个简单的相等关系产生怀疑吧!
本节目标
1.理解指数函数的概念和意义,能借助计算器或计算机画出指数函数的图象.
2.初步掌握指数函数的有关性质.
任务一:知识预习
课前预习
(1)指数函数的概念是什么?
(2)结合指数函数的图象,可归纳出指数函数具有哪些性质?
(3)指数函数的图象过哪个定点?如何求指数函数的定义域和值域?
预习课本P111~117,思考并完成以下问题
任务二:简单题型通关
课前预习
1.函数y=2x的图象是( )
D
任务二:简单题型通关
课前预习
2.函数f(x)=ax的图象经过点(1,2),则f(0)的值是________,a=________.
1
2
任务二:简单题型通关
课前预习
3.函数f(x)=2x与y轴的交点坐标为________.
(0,1)
4.函数y=(a-2)x在R上是增函数,则实数a的取值范围是________.
a>3
新知精讲
1.指数函数的定义
注意
新知精讲
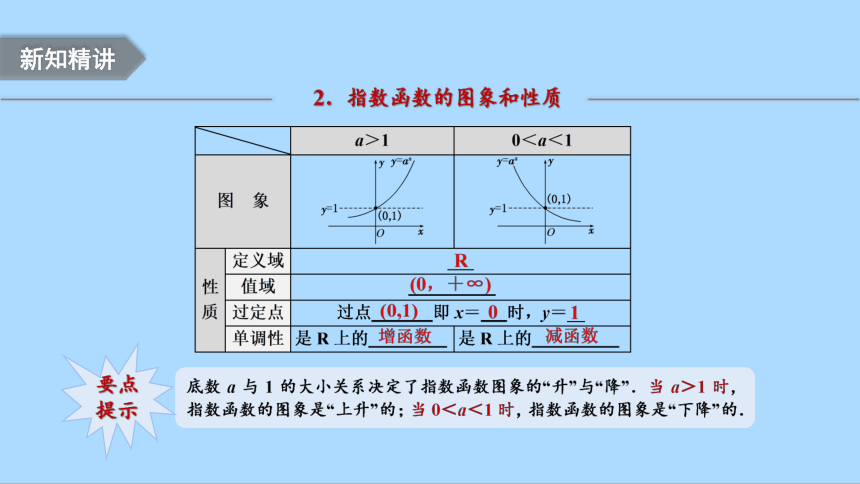
2.指数函数的图象和性质
要点提示
题型探究
题
型
一
指数函数的概念
[例1] (1)下列函数:
①y=2·3x ②y=3x+1 ③y=3x ④y=x3
其中,指数函数的个数是( )
A.0 B.1 C.2 D.3
×
×
×
√
B
题型探究
C
归纳总结
判断一个函数是否为指数函数的方法
(1)需判断其解析式是否符合y=ax(a>0,且a≠1)这一结构特征.
(2)看是否具备指数函数解析式具有的三个特征.只要有一个特征不具备,则该函数不是指数函数.
活学活用
2
题
型
二
指数函数的定义域和值域
题型探究
[例2] 求下列函数的定义域和值域
(1) y=;
(2) y=;
(3) y=
题型探究
[例2] 求下列函数的定义域和值域
(1) y= ;
题型探究
[例2] 求下列函数的定义域和值域
(2) y=;
题型探究
[例2] 求下列函数的定义域和值域
(3) y=
归纳总结
活学活用
2.求下列函数的定义域、值域:
(1) y= ; (2) y= .
活学活用
2.求下列函数的定义域、值域:
(1) y= ; (2) y= .
(2)定义域为R.
∵x2-2x-3=(x-1)2-4≥-4,
∴≤=16.
又∵>0,
∴函数y=的值域为(0,16].
题
型
三
指数型函数的图象
题型探究
题点一 指数型函数过定点问题
[例3] 1.函数y=ax-3+3(a>0,且a≠1)的图象过定点________.
小提示
指数函数y=ax(a>0,且a≠1)的图象过定点(0,1)
y=ax-3+3中,令x-3=0,得x=3,
此时y=1+3=4,
即函数y=ax-3+3的图象过定点(3,4).
(3,4)
[例3] 2.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0<a<1,b>0
D. 0<a<1,b<0
一题多联
题根显现
题型探究
题点二 指数型函数图象中数据判断
从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0<a<1;从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,所以-b>0,即b<0.
D
题型探究
题点三 作指数型函数的图象
[例3] 3. 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1) y=2x+1; (2) y=-2x.
(1)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的;
(2)y=-2x的图象与y=2x的图象关于x轴对称.
一题多联
题根显现
归纳总结
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
易错误区
换元时忽略中间变量的范围导致错误
[例4] 求函数y=++1的值域.
错解
易错误区
换元时忽略中间变量的范围导致错误
[例4] 求函数y=++1的值域.
正解
易错警示
达标检测
1.下列函数:
①y=3·5x ②y=5x+2 ③y=5x ④y=x5
其中,指数函数的个数是( )
A.0 B.1 C.2 D.3
×
×
×
√
B
达标检测
3x+1<1=30
x<-1
y=3x是增函数
x+1<0
D
达标检测
达标检测
设t=x2+1,则t≥1
y=3t≥31=3
y=3t是增函数
[3,+∞)
本课小结
1、指数函数的概念是什么?
2、指数函数具有哪些性质?
4.2 指数函数图象及其性质
高一
必修一
情景引入
某公名曰白日梦,某日向某公司老板求职,老板答应他:试用一周(7天),日工资20元。白日梦对老板说:“日工资是否能再谈一谈?”老板很随和地说:“你开个价吧!”白日梦心中暗喜,说道:“第一天您须付给我5分钱,以后每天付给的工资,第几天就是几个第一天工资相乘。”老板一听,略作思考后答应了,并叫来秘书与白日梦签订如下合同:“经双方同意,白日梦在试用期间的工资按如下方案付给:第一天付给0.05元,以后每天付给的工资,第几天就是几个第一天工资相乘。”
情景引入
签完合同后,白日梦高兴得手舞足蹈,躺在床上沾沾自喜地盘算着:第一天付给我5分,第二天付给我52=25(分),第三天付给我53=125(分),第四天付给我54=625(分)。虽然先吃了亏,可是到了第五天便可拿55=3125(分)=31.25(元);第六天就更多了,可达56分=156.25(元);第七天就更不得了,竟有57分=781.25(元)。这样一来,一星期可捞到976.55元。
次日,白日梦干起活来特别卖力,老板看在眼里,喜在心里。7天一到,秘书根据合同一算,只付给他6分钱,还说多给了半分多。白日梦一下子傻了,他搞不清楚5分与0.05元到底有何区别?!本想大挣一笔,没想到白干了7天。
情景引入
秘书的计算是:
第二天0.052=0.0025(元),第三天0.053=0.000125(元),第四天0.054=0.00000625(元),……,第七天0.057=0.00000000078125(元)。
七天共应付给:0.05+0.0025+0.000125+0.00000625+0.0000003125+0.000000015625+0.00000000078125≈
0.0526(元)。
现在如果有人问你:5分等于0.05元吗?你不得不对这个简单的相等关系产生怀疑吧!
本节目标
1.理解指数函数的概念和意义,能借助计算器或计算机画出指数函数的图象.
2.初步掌握指数函数的有关性质.
任务一:知识预习
课前预习
(1)指数函数的概念是什么?
(2)结合指数函数的图象,可归纳出指数函数具有哪些性质?
(3)指数函数的图象过哪个定点?如何求指数函数的定义域和值域?
预习课本P111~117,思考并完成以下问题
任务二:简单题型通关
课前预习
1.函数y=2x的图象是( )
D
任务二:简单题型通关
课前预习
2.函数f(x)=ax的图象经过点(1,2),则f(0)的值是________,a=________.
1
2
任务二:简单题型通关
课前预习
3.函数f(x)=2x与y轴的交点坐标为________.
(0,1)
4.函数y=(a-2)x在R上是增函数,则实数a的取值范围是________.
a>3
新知精讲
1.指数函数的定义
注意
新知精讲
2.指数函数的图象和性质
要点提示
题型探究
题
型
一
指数函数的概念
[例1] (1)下列函数:
①y=2·3x ②y=3x+1 ③y=3x ④y=x3
其中,指数函数的个数是( )
A.0 B.1 C.2 D.3
×
×
×
√
B
题型探究
C
归纳总结
判断一个函数是否为指数函数的方法
(1)需判断其解析式是否符合y=ax(a>0,且a≠1)这一结构特征.
(2)看是否具备指数函数解析式具有的三个特征.只要有一个特征不具备,则该函数不是指数函数.
活学活用
2
题
型
二
指数函数的定义域和值域
题型探究
[例2] 求下列函数的定义域和值域
(1) y=;
(2) y=;
(3) y=
题型探究
[例2] 求下列函数的定义域和值域
(1) y= ;
题型探究
[例2] 求下列函数的定义域和值域
(2) y=;
题型探究
[例2] 求下列函数的定义域和值域
(3) y=
归纳总结
活学活用
2.求下列函数的定义域、值域:
(1) y= ; (2) y= .
活学活用
2.求下列函数的定义域、值域:
(1) y= ; (2) y= .
(2)定义域为R.
∵x2-2x-3=(x-1)2-4≥-4,
∴≤=16.
又∵>0,
∴函数y=的值域为(0,16].
题
型
三
指数型函数的图象
题型探究
题点一 指数型函数过定点问题
[例3] 1.函数y=ax-3+3(a>0,且a≠1)的图象过定点________.
小提示
指数函数y=ax(a>0,且a≠1)的图象过定点(0,1)
y=ax-3+3中,令x-3=0,得x=3,
此时y=1+3=4,
即函数y=ax-3+3的图象过定点(3,4).
(3,4)
[例3] 2.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0<a<1,b>0
D. 0<a<1,b<0
一题多联
题根显现
题型探究
题点二 指数型函数图象中数据判断
从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0<a<1;从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,所以-b>0,即b<0.
D
题型探究
题点三 作指数型函数的图象
[例3] 3. 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1) y=2x+1; (2) y=-2x.
(1)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的;
(2)y=-2x的图象与y=2x的图象关于x轴对称.
一题多联
题根显现
归纳总结
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
易错误区
换元时忽略中间变量的范围导致错误
[例4] 求函数y=++1的值域.
错解
易错误区
换元时忽略中间变量的范围导致错误
[例4] 求函数y=++1的值域.
正解
易错警示
达标检测
1.下列函数:
①y=3·5x ②y=5x+2 ③y=5x ④y=x5
其中,指数函数的个数是( )
A.0 B.1 C.2 D.3
×
×
×
√
B
达标检测
3x+1<1=30
x<-1
y=3x是增函数
x+1<0
D
达标检测
达标检测
设t=x2+1,则t≥1
y=3t≥31=3
y=3t是增函数
[3,+∞)
本课小结
1、指数函数的概念是什么?
2、指数函数具有哪些性质?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
