人教A版(2019)数学必修第一册4.5.3函数模型的应用 课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册4.5.3函数模型的应用 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:49:11 | ||
图片预览











文档简介
(共34张PPT)
4.5.3 函数模型的应用
高一
必修一
本节目标
1. 指数、对数函数模型在实际问题中的应用.
2. 了解拟合函数模型,根据实际问题建立函数模型并解决实际问题.
任务一:知识预习
课前预习
(1) 指数函数模型、对数函数模型的表达形式是什么?
(2) 解决实际问题的基本过程是什么?
预习课本P148~154,思考并完成以下问题
任务二:简单题型通关
课前预习
1.某种动物繁殖数量y(单位:只)与时间x(单位:年)的关系式为y=alog2(x+1).若这种动物第1年有100只,则到第7年它们发展到( )
A.300只 B.400只
C.500只 D.600只
A
任务二:简单题型通关
课前预习
2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足( )
A.y=a(1+5%x) B.y=a+5%
C.y=a(1+5%)x-1 D.y=a(1+5%)x
D
任务二:简单题型通关
课前预习
3.已知某工厂生产某种产品的月产量y与月份x满足关系y=a·0.5x+b,现已知该厂今年1月份、2月份生产该产品分别为1万件、1.5万件,则此厂3月份该产品产量为________.
y=-2×0.5x+2
3月份产量为y=-2×0.53+2=1.75(万件)
1.75万件
1.指数函数型模型
(1)表达形式: f(x)=abx+c.
(2)条件: a,b,c为常数, a≠0, b>0, b≠1.
2.对数函数型模型
(1)表达形式: f(x)=mlogax+n.
(2)条件: m,n,a为常数, m≠0, a>0, a≠1.
新知精讲
新知精讲
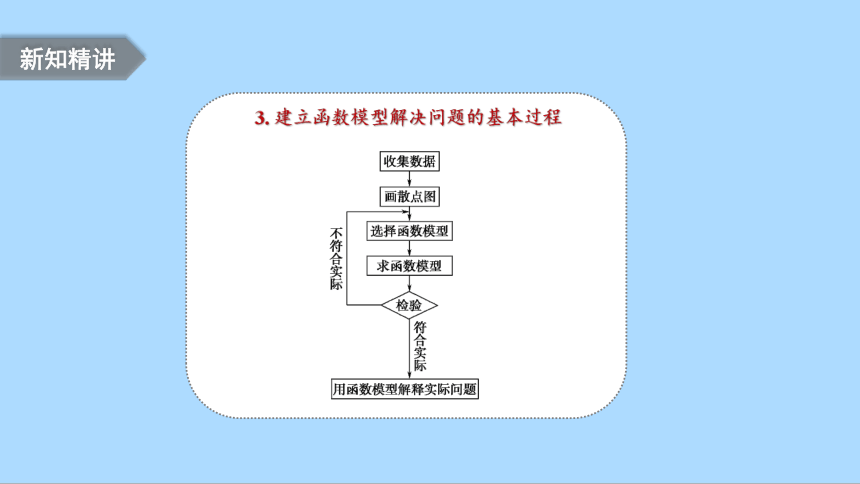
3. 建立函数模型解决问题的基本过程
新知精讲
思考:解决函数应用问题的基本步骤是什么?
利用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:
(一)审题;(二)建模;(三)求模;(四)还原.
这些步骤用框图表示如图:
题型探究
题型一
指数型函数模型的应用
题型探究
题型探究
题型探究
归纳总结
指数函数模型问题的求解策略
(1)对于增长率问题,在实际问题中常可以用指数函数模型y=N(1+p)x(其中N是基础数,p为增长率,x为时间)和幂函数模型y=a(1+x)n(其中a为基础数,x为增长率,n为时间)的形式.解题时,往往用到对数运算,要注意与已知条件中给定的值对应求解.
(2)函数y=c·akx(a,c,k为常数)是一个应用广泛的函数模型,它在电学、生物学、人口学、气象学等方面都有广泛的应用,解决这类应用题的基本方法是待定系数法,即根据题意确定相关的系数.
活学活用
题型探究
题型二
对数型函数模型的应用
题型探究
题型探究
题型探究
一题多变
1.(变问法)若本例条件不变:当一条鲑鱼的耗氧量是8 100 个单位时,它的游速是多少?
题型探究
一题多变
2.(变问法)若本例条件不变:求一条鲑鱼静止时耗氧量的单位数.
归纳总结
对数函数应用题的基本类型和求解策略
(1)基本类型:有关对数函数的应用题一般都会给出函数的解析式,然后根据实际问题求解;
(2)求解策略:首先根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据数值回答其实际意义.
活学活用
e6-1
题型探究
题型三
拟合数据构建函数模型解决实际问题
思路点拨
题型探究
题型探究
题型探究
根据所建的函数模型,
预计2019年的年产量为f(5)=1.5×5+2.5=10万件,
又年产量减少30%,即10×70%=7万件,
即2019年的年产量为7万件.
归纳总结
函数拟合与预测的一般步骤:
1 根据原始数据、表格,绘出散点图.
2 通过考察散点图,画出拟合直线或拟合曲线.
3 求出拟合直线或拟合曲线的函数关系式.
4 利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
活学活用
活学活用
以身高为横坐标,体重为纵坐标,画出散点图.
活学活用
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175 cm,体重为78 kg的在校男生的体重是否正常?
将x=175代入y=2×1.02x得y=2×1.02175,由计算器算得 y≈63.98.
由于78÷63.98≈1.22>1.2,
所以,这个男生偏胖.
达标检测
C
达标检测
2.在固定电压差(电压为常数)的前提下,当电流通过圆柱形的电线时,其电流强度I与电线半径r的三次方成正比,若已知电流通过半径为4毫米的电线时,电流强度为320安,则电流通过半径为3毫米的电线时,电流强度为( )
A.60安 B.240安
C.75安 D.135安
D
达标检测
3.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超过A万元,则超过部分按log5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
(2) 1.2+log5(2x-15)=3.2,解得x=20. 所以,小江的销售利润是20万元.
本课小结
1.函数的应用,处理问题的一般方法是根据题意,先构建函数,把所给问题转化为对函数的图象和性质的研究,从而间接求出所需要的结论.
2.解函数应用问题的步骤(四步八字)
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,建立数学模型;
(3)求模:求解数学模型,得出数学结论;
(4)还原:将数学问题还原为实际问题.
4.5.3 函数模型的应用
高一
必修一
本节目标
1. 指数、对数函数模型在实际问题中的应用.
2. 了解拟合函数模型,根据实际问题建立函数模型并解决实际问题.
任务一:知识预习
课前预习
(1) 指数函数模型、对数函数模型的表达形式是什么?
(2) 解决实际问题的基本过程是什么?
预习课本P148~154,思考并完成以下问题
任务二:简单题型通关
课前预习
1.某种动物繁殖数量y(单位:只)与时间x(单位:年)的关系式为y=alog2(x+1).若这种动物第1年有100只,则到第7年它们发展到( )
A.300只 B.400只
C.500只 D.600只
A
任务二:简单题型通关
课前预习
2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足( )
A.y=a(1+5%x) B.y=a+5%
C.y=a(1+5%)x-1 D.y=a(1+5%)x
D
任务二:简单题型通关
课前预习
3.已知某工厂生产某种产品的月产量y与月份x满足关系y=a·0.5x+b,现已知该厂今年1月份、2月份生产该产品分别为1万件、1.5万件,则此厂3月份该产品产量为________.
y=-2×0.5x+2
3月份产量为y=-2×0.53+2=1.75(万件)
1.75万件
1.指数函数型模型
(1)表达形式: f(x)=abx+c.
(2)条件: a,b,c为常数, a≠0, b>0, b≠1.
2.对数函数型模型
(1)表达形式: f(x)=mlogax+n.
(2)条件: m,n,a为常数, m≠0, a>0, a≠1.
新知精讲
新知精讲
3. 建立函数模型解决问题的基本过程
新知精讲
思考:解决函数应用问题的基本步骤是什么?
利用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:
(一)审题;(二)建模;(三)求模;(四)还原.
这些步骤用框图表示如图:
题型探究
题型一
指数型函数模型的应用
题型探究
题型探究
题型探究
归纳总结
指数函数模型问题的求解策略
(1)对于增长率问题,在实际问题中常可以用指数函数模型y=N(1+p)x(其中N是基础数,p为增长率,x为时间)和幂函数模型y=a(1+x)n(其中a为基础数,x为增长率,n为时间)的形式.解题时,往往用到对数运算,要注意与已知条件中给定的值对应求解.
(2)函数y=c·akx(a,c,k为常数)是一个应用广泛的函数模型,它在电学、生物学、人口学、气象学等方面都有广泛的应用,解决这类应用题的基本方法是待定系数法,即根据题意确定相关的系数.
活学活用
题型探究
题型二
对数型函数模型的应用
题型探究
题型探究
题型探究
一题多变
1.(变问法)若本例条件不变:当一条鲑鱼的耗氧量是8 100 个单位时,它的游速是多少?
题型探究
一题多变
2.(变问法)若本例条件不变:求一条鲑鱼静止时耗氧量的单位数.
归纳总结
对数函数应用题的基本类型和求解策略
(1)基本类型:有关对数函数的应用题一般都会给出函数的解析式,然后根据实际问题求解;
(2)求解策略:首先根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据数值回答其实际意义.
活学活用
e6-1
题型探究
题型三
拟合数据构建函数模型解决实际问题
思路点拨
题型探究
题型探究
题型探究
根据所建的函数模型,
预计2019年的年产量为f(5)=1.5×5+2.5=10万件,
又年产量减少30%,即10×70%=7万件,
即2019年的年产量为7万件.
归纳总结
函数拟合与预测的一般步骤:
1 根据原始数据、表格,绘出散点图.
2 通过考察散点图,画出拟合直线或拟合曲线.
3 求出拟合直线或拟合曲线的函数关系式.
4 利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
活学活用
活学活用
以身高为横坐标,体重为纵坐标,画出散点图.
活学活用
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175 cm,体重为78 kg的在校男生的体重是否正常?
将x=175代入y=2×1.02x得y=2×1.02175,由计算器算得 y≈63.98.
由于78÷63.98≈1.22>1.2,
所以,这个男生偏胖.
达标检测
C
达标检测
2.在固定电压差(电压为常数)的前提下,当电流通过圆柱形的电线时,其电流强度I与电线半径r的三次方成正比,若已知电流通过半径为4毫米的电线时,电流强度为320安,则电流通过半径为3毫米的电线时,电流强度为( )
A.60安 B.240安
C.75安 D.135安
D
达标检测
3.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超过A万元,则超过部分按log5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
(2) 1.2+log5(2x-15)=3.2,解得x=20. 所以,小江的销售利润是20万元.
本课小结
1.函数的应用,处理问题的一般方法是根据题意,先构建函数,把所给问题转化为对函数的图象和性质的研究,从而间接求出所需要的结论.
2.解函数应用问题的步骤(四步八字)
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,建立数学模型;
(3)求模:求解数学模型,得出数学结论;
(4)还原:将数学问题还原为实际问题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
