人教A版(2019)数学必修第一册5.3.1诱导公式(一) 课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册5.3.1诱导公式(一) 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 889.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
5.3.1 诱导公式(一)
高一
必修一
本节目标
1.了解三角函数的诱导公式的意义和作用.
2.理解诱导公式的推导过程.
3.能运用诱导公式解决一些三角函数的求值、化简和证明问题.
任务一:知识预习
课前预习
(1)π±α,-α的终边与α的终边有怎样的对称关系?
(2)诱导公式的内容是什么?
(3)诱导公式一~四有哪些结构特征?
预习课本P188~190,思考并完成以下问题
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
课前预习
任务二:简单题型通关
课前预习
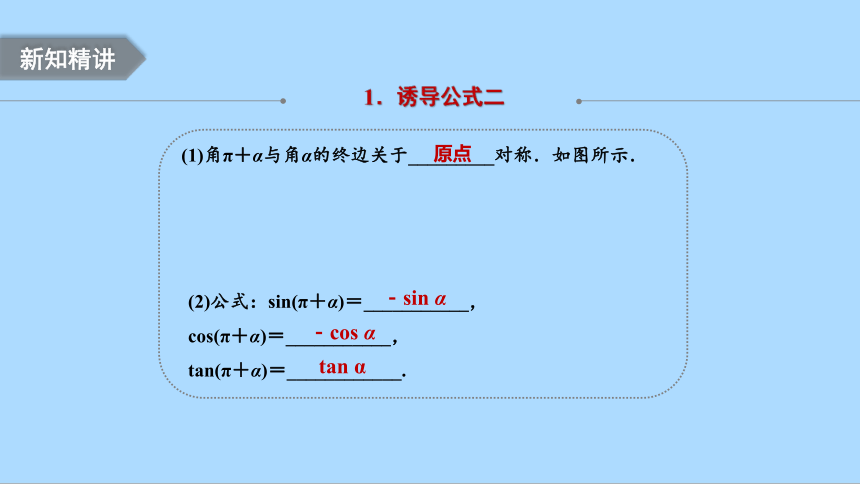
(1)角π+α与角α的终边关于_________对称.如图所示.
(2)公式:sin(π+α)=___________,
cos(π+α)=___________,
tan(π+α)=____________.
新知精讲
1.诱导公式二
原点
-sin α
-cos α
tan α
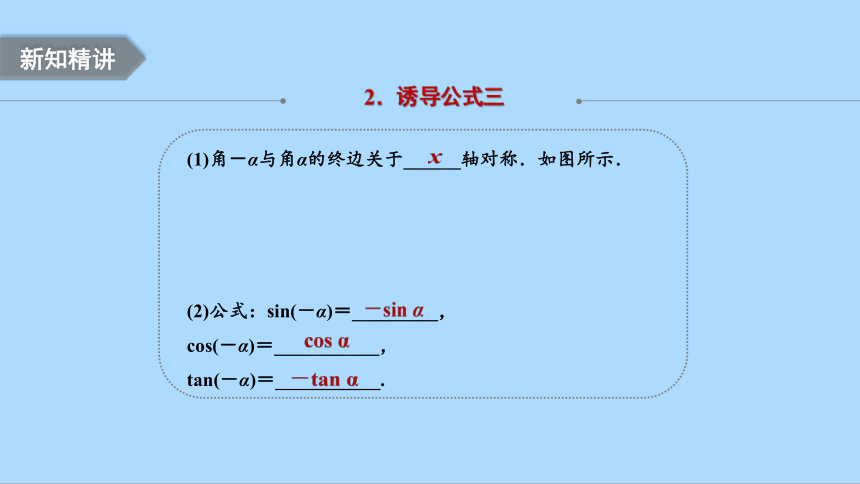
(2)公式:sin(-α)=_________,
cos(-α)=___________,
tan(-α)=___________.
(1)角-α与角α的终边关于______轴对称.如图所示.
2.诱导公式三
新知精讲
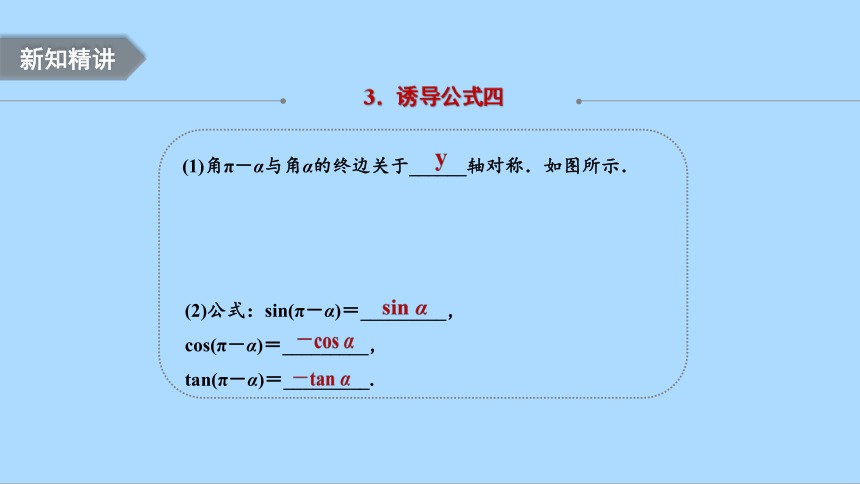
3.诱导公式四
新知精讲
(1)角π-α与角α的终边关于______轴对称.如图所示.
(2)公式:sin(π-α)=_________,
cos(π-α)=_________,
tan(π-α)=_________.
新知精讲
α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的_______函数值,前面加上把α看成_______时____________的符号.
重要结论
同名
锐角
原函数值
题型探究
题型一
给角求值问题
归纳总结
利用诱导公式解决给角求值问题的步骤
解题方法
活学活用
(2)sin(-60°)+cos 225°+tan 135°
题型探究
题型二
化简求值问题
归纳总结
利用诱导公式一~四化简应注意的问题
(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的;
(2)化简时函数名没有改变,但一定要注意函数的符号有没有改变;
(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切.
注意
活学活用
活学活用
法一
活学活用
法二
题型探究
题型三
给值求值问题
题型探究
一题多变
题型探究
一题多变
题型探究
一题多变
归纳总结
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
解决条件求值问题的策略
解题策略
达标检测
C
达标检测
②③
达标检测
本课小结
1.诱导公式的内容是什么?
2.利用诱导公式一~四化简应注意哪些问题?
3.利用诱导公式解决给角求值问题的步骤有哪些?
5.3.1 诱导公式(一)
高一
必修一
本节目标
1.了解三角函数的诱导公式的意义和作用.
2.理解诱导公式的推导过程.
3.能运用诱导公式解决一些三角函数的求值、化简和证明问题.
任务一:知识预习
课前预习
(1)π±α,-α的终边与α的终边有怎样的对称关系?
(2)诱导公式的内容是什么?
(3)诱导公式一~四有哪些结构特征?
预习课本P188~190,思考并完成以下问题
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
课前预习
任务二:简单题型通关
课前预习
(1)角π+α与角α的终边关于_________对称.如图所示.
(2)公式:sin(π+α)=___________,
cos(π+α)=___________,
tan(π+α)=____________.
新知精讲
1.诱导公式二
原点
-sin α
-cos α
tan α
(2)公式:sin(-α)=_________,
cos(-α)=___________,
tan(-α)=___________.
(1)角-α与角α的终边关于______轴对称.如图所示.
2.诱导公式三
新知精讲
3.诱导公式四
新知精讲
(1)角π-α与角α的终边关于______轴对称.如图所示.
(2)公式:sin(π-α)=_________,
cos(π-α)=_________,
tan(π-α)=_________.
新知精讲
α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的_______函数值,前面加上把α看成_______时____________的符号.
重要结论
同名
锐角
原函数值
题型探究
题型一
给角求值问题
归纳总结
利用诱导公式解决给角求值问题的步骤
解题方法
活学活用
(2)sin(-60°)+cos 225°+tan 135°
题型探究
题型二
化简求值问题
归纳总结
利用诱导公式一~四化简应注意的问题
(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的;
(2)化简时函数名没有改变,但一定要注意函数的符号有没有改变;
(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切.
注意
活学活用
活学活用
法一
活学活用
法二
题型探究
题型三
给值求值问题
题型探究
一题多变
题型探究
一题多变
题型探究
一题多变
归纳总结
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
解决条件求值问题的策略
解题策略
达标检测
C
达标检测
②③
达标检测
本课小结
1.诱导公式的内容是什么?
2.利用诱导公式一~四化简应注意哪些问题?
3.利用诱导公式解决给角求值问题的步骤有哪些?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
