人教A版(2019)数学必修第一册5.7.1三角函数的应用 课件(共26张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册5.7.1三角函数的应用 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 992.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:54:39 | ||
图片预览








文档简介
(共26张PPT)
5.7.1 三角函数的应用
高一
必修一
本节目标
1.了解y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、初相.
2.能根据y=Asin(ωx+φ)的部分图象,确定其解析式.
任务一:知识预习
课前预习
预习课本P242~244,思考并完成以下问题
(1)在简谐运动中,y=Asin(ωx+φ)的初相、振幅、周期分别为多少?
(2)函数y=Asin(ωx+φ)有哪些性质?
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
课前预习
A
新知精讲
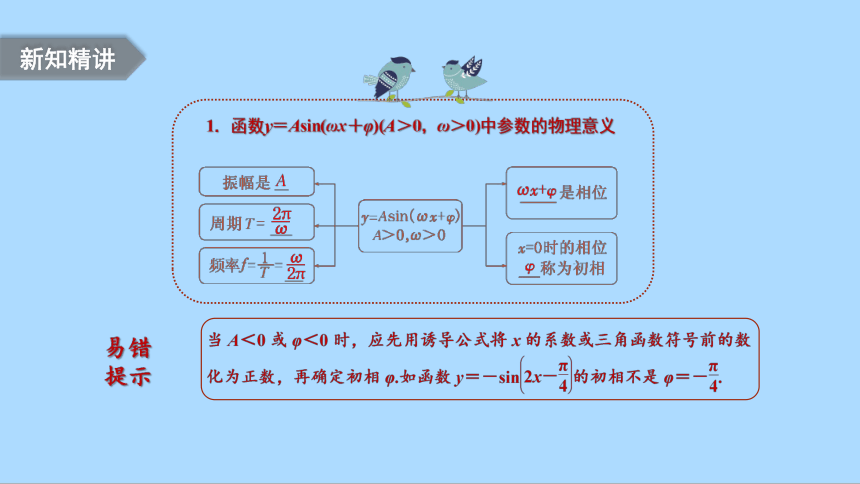
1.函数y=Asin(ωx+φ)(A>0,ω>0)中参数的物理意义
易错提示
新知精讲
2.函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
题型探究
题型一 函数y=Asin(ωx+φ)中参数的物理意义
归纳总结
首先把函数解析式化为y=Asin(ωx+φ)(其中A>0,ω>0)的形式,再求振幅、周期、初相.应注意A>0,ω>0.
方法总结
活学活用
A
活学活用
题型探究
题型二
由图象确定函数的解析式
法一
逐一定参法
题型探究
题型二
由图象确定函数的解析式
法二
待定系数法
题型探究
题型二
由图象确定函数的解析式
法三
图象变换法
归纳总结
给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法
活学活用
法一
活学活用
法二
题型三 函数y=Asin(cos x+φ)的性质的应用
题型探究
题型探究
一题多变
思维发散
1.[变条件] 将本例中“sin”改为“cos”,其他条件不变,结果如何?
题型探究
一题多变
思维发散
2.[变条件,变设问] 将本例中对称中心改为对称轴,其他条件不变,求离y轴最近的一条对称轴方程.
达标检测
D
达标检测
2.函数f(x)=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图所示,则( )
C
达标检测
π
达标检测
本课小结
1.函数y=Asin(ωx+φ)有哪些性质?
2.给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法.
5.7.1 三角函数的应用
高一
必修一
本节目标
1.了解y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、初相.
2.能根据y=Asin(ωx+φ)的部分图象,确定其解析式.
任务一:知识预习
课前预习
预习课本P242~244,思考并完成以下问题
(1)在简谐运动中,y=Asin(ωx+φ)的初相、振幅、周期分别为多少?
(2)函数y=Asin(ωx+φ)有哪些性质?
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
课前预习
A
新知精讲
1.函数y=Asin(ωx+φ)(A>0,ω>0)中参数的物理意义
易错提示
新知精讲
2.函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
题型探究
题型一 函数y=Asin(ωx+φ)中参数的物理意义
归纳总结
首先把函数解析式化为y=Asin(ωx+φ)(其中A>0,ω>0)的形式,再求振幅、周期、初相.应注意A>0,ω>0.
方法总结
活学活用
A
活学活用
题型探究
题型二
由图象确定函数的解析式
法一
逐一定参法
题型探究
题型二
由图象确定函数的解析式
法二
待定系数法
题型探究
题型二
由图象确定函数的解析式
法三
图象变换法
归纳总结
给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法
活学活用
法一
活学活用
法二
题型三 函数y=Asin(cos x+φ)的性质的应用
题型探究
题型探究
一题多变
思维发散
1.[变条件] 将本例中“sin”改为“cos”,其他条件不变,结果如何?
题型探究
一题多变
思维发散
2.[变条件,变设问] 将本例中对称中心改为对称轴,其他条件不变,求离y轴最近的一条对称轴方程.
达标检测
D
达标检测
2.函数f(x)=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图所示,则( )
C
达标检测
π
达标检测
本课小结
1.函数y=Asin(ωx+φ)有哪些性质?
2.给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
