5.2.1三角函数的概念(2) 课件(共16张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念(2) 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 704.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 22:59:49 | ||
图片预览





文档简介
(共16张PPT)
三角函数的概念
(2)
教学目标 知识目标 1.能利用三角函数的定义,判断正弦、余弦、正切函数值在各象限内的符号.
2.通过任意角的三角函数的定义理解终边相同角的同一三角函数值相等.
素养目标 通过利用三角函数的定义对各象限角的三角函数 值的符号分析和公式一的应用, 增强学生数学抽象、直观想象、数学运算和逻辑推理的核心素养.
教学重点 正弦、余弦、正切函数值在各象限内的符号;终边相同角的同一三角函数值间的关系.
教学难点 正确理解三角函数可看作以“实数”为自变量的函数
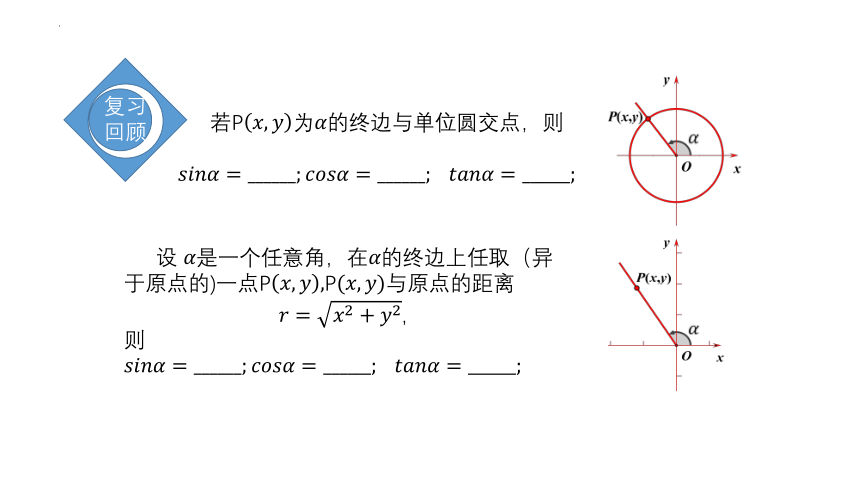
设 是一个任意角,在的终边上任取(异于原点的)一点PP与原点的距离
,
则
若P的终边与单位圆交点,则
复习
回顾
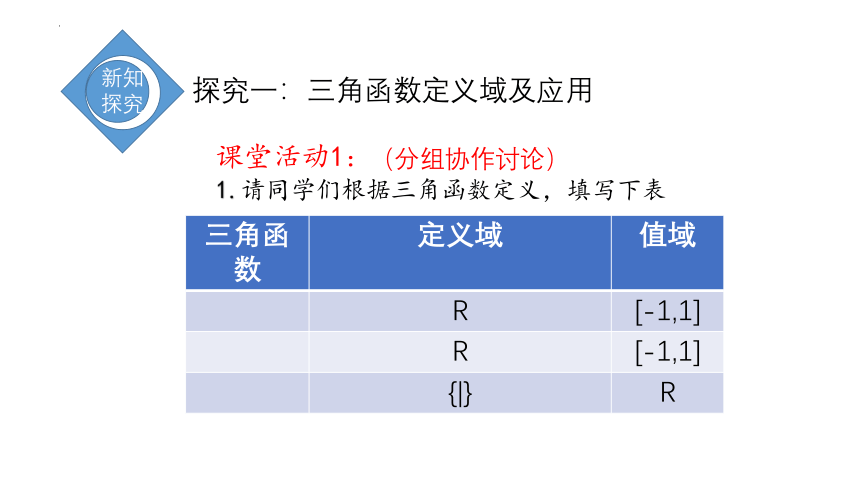
课堂活动1:(分组协作讨论)
1.请同学们根据三角函数定义,填写下表
三角函数 定义域 值域
R [-1,1]
R [-1,1]
{|} R
探究一:三角函数定义域及应用
新知
探究
有意义的的取值范围
解:由题意得解得:
即:
所以,当时, 有意义
3. 求函数
的定义域.
解:,
,
,
定义域为
,
分析:
1.学生很容易得到不等式
2.解是难点,可借助下图结合三角函数定义加以突破.
通过此题可使学生加深对三角函数定义的理解.
课堂活动二(分组协作讨论)
请同学们根据三角函数定义,分析c、 在各象限内的值的性质符号,并将结果填入对应各图中.
探究二:三角函数值在各象限内的性质符号
新知
探究
课堂活动三(分组协作讨论)
问题:设.请你根据三角函数定义,判断与、与与是否分别相等?
终边相同的角的同一三角函数值相等
=
=
=
其中
新知
探究
1.确定下列三角函数的符号:
(1) (2)
(3) (4)
1.本题考查了三角函数值的符号,准确判断角的终边的位置是解决问题的关键.
2.对于、需要利用共终边角转化再判断角度所在象限或者轴线角.
应用
新知
课堂活动四(分组协作讨论)
解:是第三象限角.
是第四象限角.
,而是第一象限角.
,而的终边在轴上, .
课堂活动五(分组协作讨论)
确定下列各式的符号:
(1) 2 2; (2) 3 4 5.
解:是第二象限角,,,
;
是第二象限角,,
是第三象限角,,
是第四象限角,,
.
本题难点在于角的弧度数均不含故对学生造成干扰,教师应进一步强调任意实数都表示角.可将其与、等进行比较.
课堂活动六(分组协作讨论)
求证:角为第三象限角的充要条件是
证明:必要性:∵θ是第三象限角,?
∴
充分性:∵sinθ<0,
∴θ是第三或第四象限角或终边在y轴的非正半轴上
∵tanθ>0,∴θ是第一或第三象限角.?
∵sinθ<0,tanθ>0都成立.?
∴θ为第三象限角.?
课堂活动七(分组协作讨论)
求下列三角函数值.
(1) (2) (3)
解:1. =
=
本节课我们重点讨论了两个内容:
1. 三角函数在各象限内的符号
2. 终边相同的角的同一三角函数值的关系.即=
=
=
通过这组公式可将任意角的三角函数化为0°到360°角的三角函数.
课堂
小结
课后
练习
1.点P()落在( )
第一象限内 B. 第二象限内
C. 第三象限内 D. 第四象限内
2.函数的值域是( )
{-1,0,1,3} B. {-1,0,3}
C. {-1,3} D. {-1,1}
3.求值
解:
原式
三角函数的概念
(2)
教学目标 知识目标 1.能利用三角函数的定义,判断正弦、余弦、正切函数值在各象限内的符号.
2.通过任意角的三角函数的定义理解终边相同角的同一三角函数值相等.
素养目标 通过利用三角函数的定义对各象限角的三角函数 值的符号分析和公式一的应用, 增强学生数学抽象、直观想象、数学运算和逻辑推理的核心素养.
教学重点 正弦、余弦、正切函数值在各象限内的符号;终边相同角的同一三角函数值间的关系.
教学难点 正确理解三角函数可看作以“实数”为自变量的函数
设 是一个任意角,在的终边上任取(异于原点的)一点PP与原点的距离
,
则
若P的终边与单位圆交点,则
复习
回顾
课堂活动1:(分组协作讨论)
1.请同学们根据三角函数定义,填写下表
三角函数 定义域 值域
R [-1,1]
R [-1,1]
{|} R
探究一:三角函数定义域及应用
新知
探究
有意义的的取值范围
解:由题意得解得:
即:
所以,当时, 有意义
3. 求函数
的定义域.
解:,
,
,
定义域为
,
分析:
1.学生很容易得到不等式
2.解是难点,可借助下图结合三角函数定义加以突破.
通过此题可使学生加深对三角函数定义的理解.
课堂活动二(分组协作讨论)
请同学们根据三角函数定义,分析c、 在各象限内的值的性质符号,并将结果填入对应各图中.
探究二:三角函数值在各象限内的性质符号
新知
探究
课堂活动三(分组协作讨论)
问题:设.请你根据三角函数定义,判断与、与与是否分别相等?
终边相同的角的同一三角函数值相等
=
=
=
其中
新知
探究
1.确定下列三角函数的符号:
(1) (2)
(3) (4)
1.本题考查了三角函数值的符号,准确判断角的终边的位置是解决问题的关键.
2.对于、需要利用共终边角转化再判断角度所在象限或者轴线角.
应用
新知
课堂活动四(分组协作讨论)
解:是第三象限角.
是第四象限角.
,而是第一象限角.
,而的终边在轴上, .
课堂活动五(分组协作讨论)
确定下列各式的符号:
(1) 2 2; (2) 3 4 5.
解:是第二象限角,,,
;
是第二象限角,,
是第三象限角,,
是第四象限角,,
.
本题难点在于角的弧度数均不含故对学生造成干扰,教师应进一步强调任意实数都表示角.可将其与、等进行比较.
课堂活动六(分组协作讨论)
求证:角为第三象限角的充要条件是
证明:必要性:∵θ是第三象限角,?
∴
充分性:∵sinθ<0,
∴θ是第三或第四象限角或终边在y轴的非正半轴上
∵tanθ>0,∴θ是第一或第三象限角.?
∵sinθ<0,tanθ>0都成立.?
∴θ为第三象限角.?
课堂活动七(分组协作讨论)
求下列三角函数值.
(1) (2) (3)
解:1. =
=
本节课我们重点讨论了两个内容:
1. 三角函数在各象限内的符号
2. 终边相同的角的同一三角函数值的关系.即=
=
=
通过这组公式可将任意角的三角函数化为0°到360°角的三角函数.
课堂
小结
课后
练习
1.点P()落在( )
第一象限内 B. 第二象限内
C. 第三象限内 D. 第四象限内
2.函数的值域是( )
{-1,0,1,3} B. {-1,0,3}
C. {-1,3} D. {-1,1}
3.求值
解:
原式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
