2012—2013学年度第一学期期末考试九年级数学试题
文档属性
| 名称 | 2012—2013学年度第一学期期末考试九年级数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-19 12:34:53 | ||
图片预览

文档简介
2012—2013学年度第一学期期末考试九年级数学试题
一、选择题
1.二次函数y=4(x-1)2+2的顶点坐标是( )A.(-1,2) B.(-1,-2) C.(1,2) D(1,-2)
2.如图所示的物体由两个紧靠在一起的圆柱体组成,它的主视图是( )
3.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )A.30° B.45° C.60° D.90°
4.在△ABC中,(2sinA-1)2+=0,则△ABC的形状为( )
A.等腰三角形 B. 等边三角形 C.直角三角形 D.等腰直角三角形
5.已知两圆半径、分别是方程的两根,两圆的圆心距为7,则两圆的位置关系是( )A. 相交 B. 内切 C.外离 D.外切
6. 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥的侧面(如图所示),则这个圆锥的底面半径是( )A.2cm B.3cm C.4cm D.5cm
7.要用圆形铁片截出边长为a的正六边形铁片,则选用铁片的直径至少为( )
A. a B.2a C.a D.2a
8.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧 上一点,若
∠ABC =32°,则∠P的度数为( )A.28° B.26° C.35° D.32°
9. 二次函数y=ax2+bx+c(a≠0)的图像如图所示,其对称轴为x=1,有下列结论: ①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根为x1,x2,则x1+x2=2.则正确的结论是( )A.①② B. ①③ C.③④ D.②④
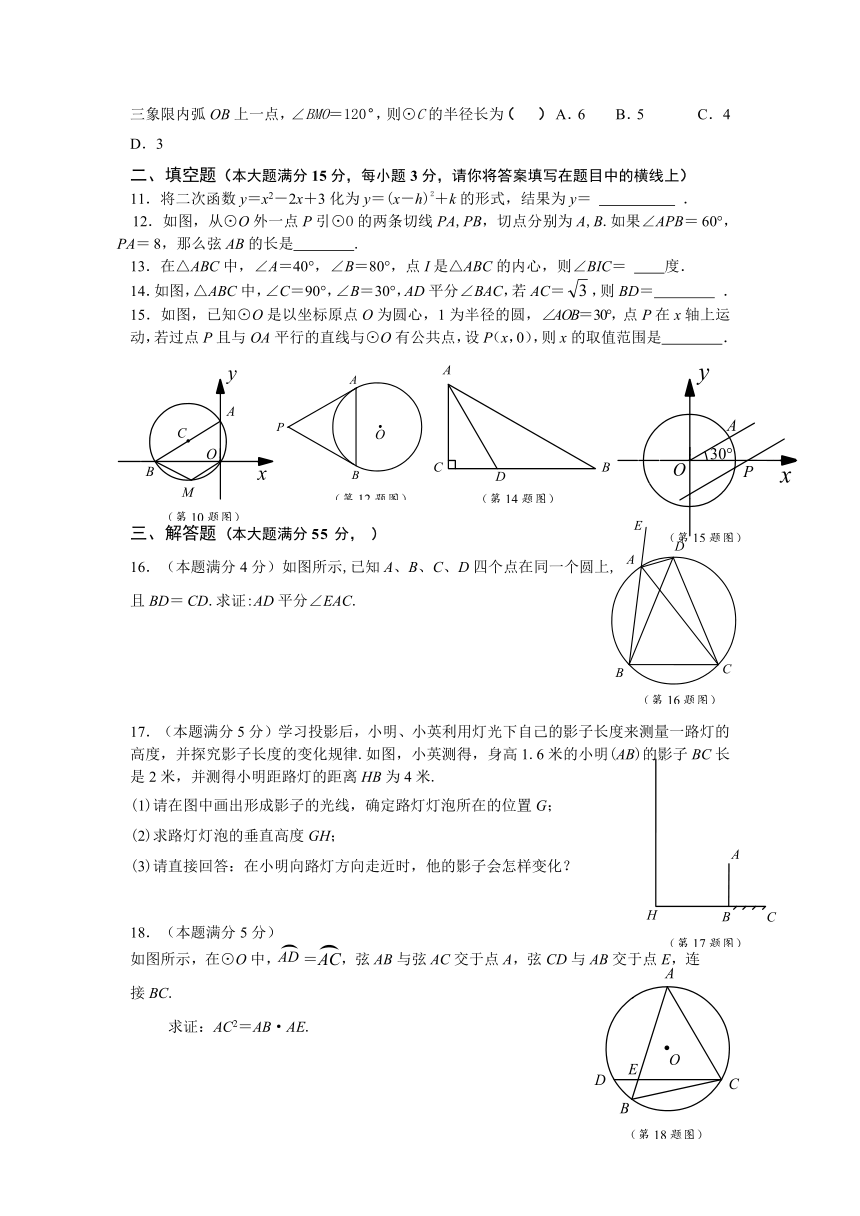
10.如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径长为( ) A.6 B.5 C. 4 D.3
二、填空题(本大题满分15分,每小题3分,请你将答案填写在题目中的横线上)
11.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为y= .
12.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是 .
13.在△ABC中,∠A=40°,∠B=80°,点I是△ABC的内心,则∠BIC= 度.
14.如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,若AC=,则BD= .
15.如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=30°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是 .
三、解答题 (本大题满分55分, )
16.(本题满分4分)如图所示,已知A、B、C、D四个点在同一个圆上,
且BD=CD.求证:AD平分∠EAC.
17.(本题满分5分)学习投影后,小明、小英利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,小英测得,身高1.6米的小明(AB)的影子BC长是2米,并测得小明距路灯的距离HB为4米.
(1)请在图中画出形成影子的光线,确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)请直接回答:在小明向路灯方向走近时,他的影子会怎样变化?
18.(本题满分5分)
如图所示,在⊙O中, = ,弦AB与弦AC交于点A,弦CD与AB交于点E,连接BC.
求证:AC2=AB·AE.
19.(本题满分6分)将一条长为20cm的铁丝剪成两截,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形边长分别为多少时,正方形面积之和最小?
20.(本题满分6分)如图,已知⊙O的直径AB与弦CD相交于点E,且DE=CE,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF.
(2)若⊙O半径为5,cos∠BCD=,求弦AD的长.
21.(本题满分6分)
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为.
(1)求弦CD的长.
(2)求阴影部分面积.
22.(本题满分7分)
小明家窗户向南,窗户AB的高度为2米,他想为自己家的窗户设计一个直角形遮阳篷BCD(如图),若想当冬至太阳光线与地面夹角26°时,使太阳光刚好全部射入室内,当夏至太阳光线与地面夹角64°时使太阳光刚好不射入室内.请你借助下面的图形②,帮助小明算一算,遮阳篷BCD中,BC和CD的长各是多少?(精确到0.01米)
(sin26°≈0.45,cos26°≈0.9,tan26°≈0.5, sin64°≈0.90,cos64°≈0.45,tan64°≈2.0 )
23.(本题满分8分)如图,C是以AB为直径的⊙O上一点,P为B A延长线上一点,过点A作⊙O的切线交PC于F,OF交AC于点E,且AF=FC.
(1)求证:PC是⊙O的切线.
(2)若PA=3,AB=9,求PC的长.
24.(本题满分8分)
如图所示,在平面直角坐标系Oxy中,已知点A(﹣,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由.
(第2题图)
(第9题图)
(第3题图)
(第8题图)
(第6题图)
(第15题图)
(第10题图)
(第14题图)
(第12题图)
(第16题图)
(第17题图)
(第18题图)
(第20题图)
(第21题图)
(第22题图①)
(第22题图②)
(第23题图)
(第24题图)
(第24题备用图)
一、选择题
1.二次函数y=4(x-1)2+2的顶点坐标是( )A.(-1,2) B.(-1,-2) C.(1,2) D(1,-2)
2.如图所示的物体由两个紧靠在一起的圆柱体组成,它的主视图是( )
3.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )A.30° B.45° C.60° D.90°
4.在△ABC中,(2sinA-1)2+=0,则△ABC的形状为( )
A.等腰三角形 B. 等边三角形 C.直角三角形 D.等腰直角三角形
5.已知两圆半径、分别是方程的两根,两圆的圆心距为7,则两圆的位置关系是( )A. 相交 B. 内切 C.外离 D.外切
6. 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥的侧面(如图所示),则这个圆锥的底面半径是( )A.2cm B.3cm C.4cm D.5cm
7.要用圆形铁片截出边长为a的正六边形铁片,则选用铁片的直径至少为( )
A. a B.2a C.a D.2a
8.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧 上一点,若
∠ABC =32°,则∠P的度数为( )A.28° B.26° C.35° D.32°
9. 二次函数y=ax2+bx+c(a≠0)的图像如图所示,其对称轴为x=1,有下列结论: ①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根为x1,x2,则x1+x2=2.则正确的结论是( )A.①② B. ①③ C.③④ D.②④
10.如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径长为( ) A.6 B.5 C. 4 D.3
二、填空题(本大题满分15分,每小题3分,请你将答案填写在题目中的横线上)
11.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为y= .
12.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是 .
13.在△ABC中,∠A=40°,∠B=80°,点I是△ABC的内心,则∠BIC= 度.
14.如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,若AC=,则BD= .
15.如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=30°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是 .
三、解答题 (本大题满分55分, )
16.(本题满分4分)如图所示,已知A、B、C、D四个点在同一个圆上,
且BD=CD.求证:AD平分∠EAC.
17.(本题满分5分)学习投影后,小明、小英利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,小英测得,身高1.6米的小明(AB)的影子BC长是2米,并测得小明距路灯的距离HB为4米.
(1)请在图中画出形成影子的光线,确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)请直接回答:在小明向路灯方向走近时,他的影子会怎样变化?
18.(本题满分5分)
如图所示,在⊙O中, = ,弦AB与弦AC交于点A,弦CD与AB交于点E,连接BC.
求证:AC2=AB·AE.
19.(本题满分6分)将一条长为20cm的铁丝剪成两截,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形边长分别为多少时,正方形面积之和最小?
20.(本题满分6分)如图,已知⊙O的直径AB与弦CD相交于点E,且DE=CE,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF.
(2)若⊙O半径为5,cos∠BCD=,求弦AD的长.
21.(本题满分6分)
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为.
(1)求弦CD的长.
(2)求阴影部分面积.
22.(本题满分7分)
小明家窗户向南,窗户AB的高度为2米,他想为自己家的窗户设计一个直角形遮阳篷BCD(如图),若想当冬至太阳光线与地面夹角26°时,使太阳光刚好全部射入室内,当夏至太阳光线与地面夹角64°时使太阳光刚好不射入室内.请你借助下面的图形②,帮助小明算一算,遮阳篷BCD中,BC和CD的长各是多少?(精确到0.01米)
(sin26°≈0.45,cos26°≈0.9,tan26°≈0.5, sin64°≈0.90,cos64°≈0.45,tan64°≈2.0 )
23.(本题满分8分)如图,C是以AB为直径的⊙O上一点,P为B A延长线上一点,过点A作⊙O的切线交PC于F,OF交AC于点E,且AF=FC.
(1)求证:PC是⊙O的切线.
(2)若PA=3,AB=9,求PC的长.
24.(本题满分8分)
如图所示,在平面直角坐标系Oxy中,已知点A(﹣,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由.
(第2题图)
(第9题图)
(第3题图)
(第8题图)
(第6题图)
(第15题图)
(第10题图)
(第14题图)
(第12题图)
(第16题图)
(第17题图)
(第18题图)
(第20题图)
(第21题图)
(第22题图①)
(第22题图②)
(第23题图)
(第24题图)
(第24题备用图)
同课章节目录
