6.1 平均数课时练习题（含答案）

中小学教育资源及组卷应用平台
北师大版八年级数学上册第六章第1节《平均数》课时练习题（含答案）
一、单选题
1．数据10，3，a，7，5的平均数是6，则a等于（　 　）．
A．3 B．4 C．5 D．6
2．如果与的平均数是5，那与的平均数是（ ）
A．4 B．5 C．6 D．7
3．若一组数据3、4、5、x、6、7的平均数是5，则x的值是（ ）
A．4 B．5 C．6 D．7
4．为了满足顾客的需求，某商场将5kg奶糖，3kg酥心糖和2kg水果糖混合成什锦糖出售．已知奶糖的售价为每千克40元，酥心糖为每千克20元，水果糖为每千克15元，混合后什锦糖的售价应为每千克（　　）
A．25元 B．28.5元 C．29元 D．34.5元
5．某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核（考核的满分均为100分），三个方面的重要性之比依次为3：5：2．小王经过考核后所得的各项分数依次为90、88、85分，那么小王的最后综合得分是（　　）
A．87 B．87.5 C．87.6 D．88
6．小刘利用空闲时间到外地某建筑公司打工，公司承诺：正常上班的工资为200元/天，不能正常上班（如下雨）的工资为80元/天，如果某月（30天）正常上班的天数占80%，则当月小刘的日平均工资为（ ）
A．140元 B．160元 C．176元 D．182元
7．六位同学的年龄分别是13、14、15、14、14、15岁，关于这组数据，正确说法是（ ）
A．平均数是14 B．中位数是14.5 C．方差3 D．众数是14
8．在某次演讲比赛中，五位评委给选手圆圆打分，得到互不相等的五个分数．若去掉一个最高分，平均分为x；去掉一个最低分，平均分为y；同时去掉一个最高分和一个最低分，平均分为z，则（　　）
A．y＞z＞x B．x＞z＞y C．y＞x＞z D．z＞y＞x
二、填空题
9．如果一组数据中有3个6、4个，2个、1个0和3个x，其平均数为x，那么______．
10．已知一组数据10、3、a、5的平均数为5，那么a为_____．
11．某校招聘教师，规定综合成绩由笔试成绩和面试成绩构成，其中笔试占60%，面试占40%，有一名应聘者的综合成绩为84分，笔试成绩是80分，则面试成绩为______分．
12．若已知数据，，的平均数为，那么数据，，的平均数为______（用含的代数式表示）．
13．已知数据，，， 的平均数为10，则数据，，，的平均数是______．
14．每年的4月23日是“世界读书日”，某校为了解4月份八年级学生的读书情况，随机调查了八年级50名学生读书的册数，数据整理如下：
册数 0 1 2 3 4
人数 9 3 20 15 3
由此估计该校八年级学生4月份人均读书______册．
三、解答题
15．某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平、艺术水平、组织能力的测试，根据综合成绩择优录取．他们的各项成绩（单项满分100分）如表所示：
候选人 文化水平 艺术水平 组织能力
甲 80分 87分 82分
乙 80分 96分 76分
(1)如果把各项成绩的平均数作为综合成绩，应该录取谁？
(2)如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计入综合成绩，应该录取谁？
16．中华文化源远流长，中华诗词寓意深广，为了传承优秀传统文化，我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩不低于50分，为了更好地了解本次海选比赛的成绩分布情况．随机选取其中200名学生的海选比赛成绩（总分100分）作为样本进行整理，得到海选成绩统计表与扇形统计图如下：
抽取的200名学生成绩统计表
组别 海选成绩 人数
A组 10
B组 30
C组 40
D组 a
E组 70
请根据所给信息解答下列问题：
(1)填空：①____________，②____________，③____________度；
(2)若把统计表每组中各个成绩用这组数据的中间值代替（例如：A组数据中间值为55分），请估计被选取的200名学生成绩的平均数；
(3)规定海选成绩不低于90分记为“优秀”，请估计该校参加这次海选比赛的2000名学生中成绩“优秀”的有多少人？
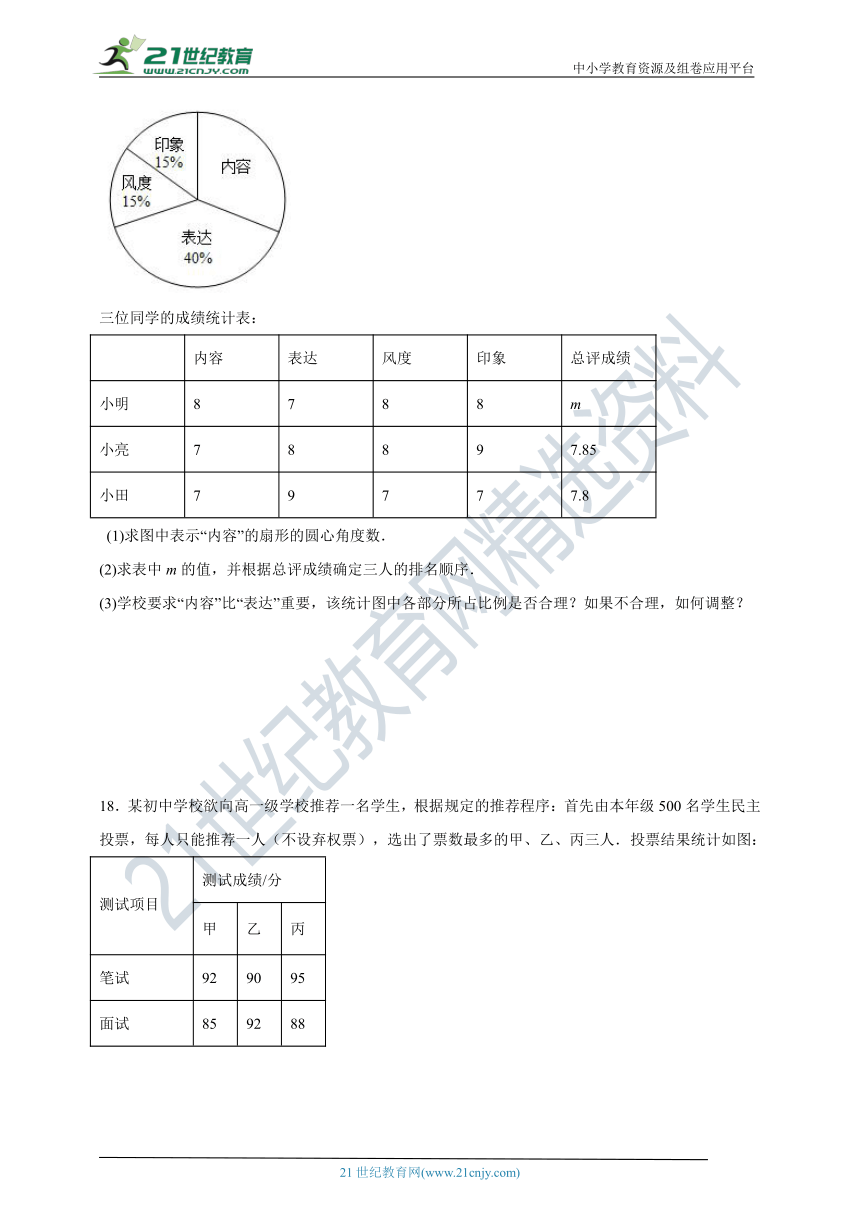
17．学校举办演讲比赛，总评成绩由“内容、表达、风度、印象”四部分组成．九（1）班组织选拔赛，制定的各部分所占比例如图，三位同学的成绩如表．请解答下列问题：
演讲总评成绩各部分所占比例的统计图：
三位同学的成绩统计表：
内容 表达 风度 印象 总评成绩
小明 8 7 8 8 m
小亮 7 8 8 9 7.85
小田 7 9 7 7 7.8
(1)求图中表示“内容”的扇形的圆心角度数．
(2)求表中m的值，并根据总评成绩确定三人的排名顺序．
(3)学校要求“内容”比“表达”重要，该统计图中各部分所占比例是否合理？如果不合理，如何调整？
18．某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级500名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人．投票结果统计如图：
测试项目 测试成绩/分
甲 乙 丙
笔试 92 90 95
面试 85 92 88
其次，对三名候选人进行了笔试和面试两项测试．各项成绩如表所示，请你根据以上信息解答下列问题：
(1)请计算每名候选人的得票数；
(2)若每名候选人得一票记0.5分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？
19．某学校对九年级共500名男生进行体能测试．从中任意选取40名的测试成绩进行分析，分为甲，乙两组，绘制出如下的统计表和统计图（成绩均为整数，满分为10分）．
甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
请根据上面的信息，解答下列问题：
(1)______：
(2)从平均分角度看，评价甲，乙两个小组的成绩；
(3)估计该校男生在这次体能测试中拿满分的人数．
20．从甲、乙两个企业随机抽取部分职工，对某个月月收入情况进行调查，并把调查结果分别制成扇形统计图和条形统计图．
(1)在扇形统计图中，“6千元”所在的扇形的圆心角是 　 　；
(2)在乙企业抽取的部分职工中，随机选择一名职工，求该职工月收入超过5千元的概率；
(3)若要比较甲、乙两家企业抽取的职工的平均工资，小明提出自己的看法：虽然不知道甲企业抽取职工的人数，但是可以根据加权平均数计算甲企业抽取的职工的平均工资，因此可以比较；小明的说法正确吗？若正确，请比较甲企业抽取的职工的平均工资与乙企业抽取的职工的平均工资的多少；若不正确，请说明理由。
参考答案
1．C2．D3．B4．C5．D6．C7．D8．A
9．1
10．2
11．
12．##
13．12.5
14．2
15．（1）解：甲的综合成绩为（分），
乙的综合成绩为（分）．
因为乙的综合成绩比甲的高，所以应该录取乙；
（2）
解：甲的综合成绩为（分），
乙的综合成绩为（分）．
因为甲的综合成绩比乙的高，所以应该录取甲．
16．（1）解：（人）；
；．
故答案为：；；
（2）
被选取的200名学生成绩的平均数为：
；
答：估计被选取的200名学生成绩的平均数是82；
（3）
（人）．
答：估计该校参加这次海选比赛的2000名学生中成绩“优秀”的有700人．
17．（1）解：∵“内容”所占比例为，
∴“内容”的扇形的圆心角；
（2）
解：，
∵，
∴三人成绩从高到低的排名顺序为：小亮，小田，小明；
（3）
解：各部分所占比例不合理，
“内容”比“表达”重要，那么“内容”所占比例应大于“表达”所占比例，
∴“内容”所占百分比应为40%，“表达”所占百分比为30%，其它不变；
18．（1）解：甲的票数是：500×34%=170（票），
乙的票数是：500×（1-34%-28%-8%）=150（票），
丙的票数是：500×28%=140（票）．
（2）
解：甲的平均成绩：=88.5（分），
乙的平均成绩：=87.6（分），
丙的平均成绩：=83.4（分）．
∵甲的平均成绩最高，
∴应该录取甲．
19．（1）解：，
故答案为：3．
（2）
（分），
（分），
∵，
∴甲组成绩比乙组好．
（3）
选取40名的测试成绩中，满分人数为（人），
∴估计该校男生在这次体能测试中拿满分的人数为（人）
∴答案为：100人．
20．（1）解：360°×（1 10% 10% 20% 20%）＝144°，
故答案为：144°；
（2）由条形图可得：乙企业共抽取10人，其中月收入超过5千元的有3人，
∴该职工月收入超过5千元的概率为：；
（3）小明的说法正确，
设甲企业的调查人数为m，
∵“6千元”所占的百分比为：1 10% 10% 20% 20%＝40%，
∴甲企业的平均工资为：×（20%m×5＋10%m×4＋10%m×8＋20%m×7＋40%m×6）＝6（千元），
乙企业的平均工资为：＝6（千元），
∴甲企业的平均工资与乙企业的平均工资相等．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)