【精选备课】2022-2023学年华师大版数学七年级上册 4.5.2 线段的长短比较 课件(共20张PPT)
文档属性
| 名称 | 【精选备课】2022-2023学年华师大版数学七年级上册 4.5.2 线段的长短比较 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 757.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 11:15:25 | ||
图片预览








文档简介
(共20张PPT)
4.5.2 线段的长短比较
教学目标
1、掌握分别用测量与重叠来比较线段大小的方法;
2、充分理解两条线段大小比较所隐含的意义,能从“量”与“形”上进行转化;
3、线段中点的性质及其简单运算。
教学重难点
学习重点:线段大小比较的方法及其原理;
学习难点:从“数量”的角度到从“形”的角度来分析两条线段的大小比较。
复习回顾
1、
2、什么叫两点间的距离?
3、直线、线段的公理是什么?
有几个端点 向几个方向延伸 能否度量
直线
射线
线段
问题思考
(1)你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示 来比较两条线段的长短吗?讨论后派一位代表上来说说你们的想法。
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
线段的比较:
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
0
A
B
D
C
(1)如果点B在线段CD上,
记作ABA
B
D
C
(2)如果点B在线段CD的延长线上, 记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
第二种方法:叠合法
注意:起点对齐,看终点
比较线段长短的两种方法:
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
(1)
a
b
(3)
(2)
a
b
a
b
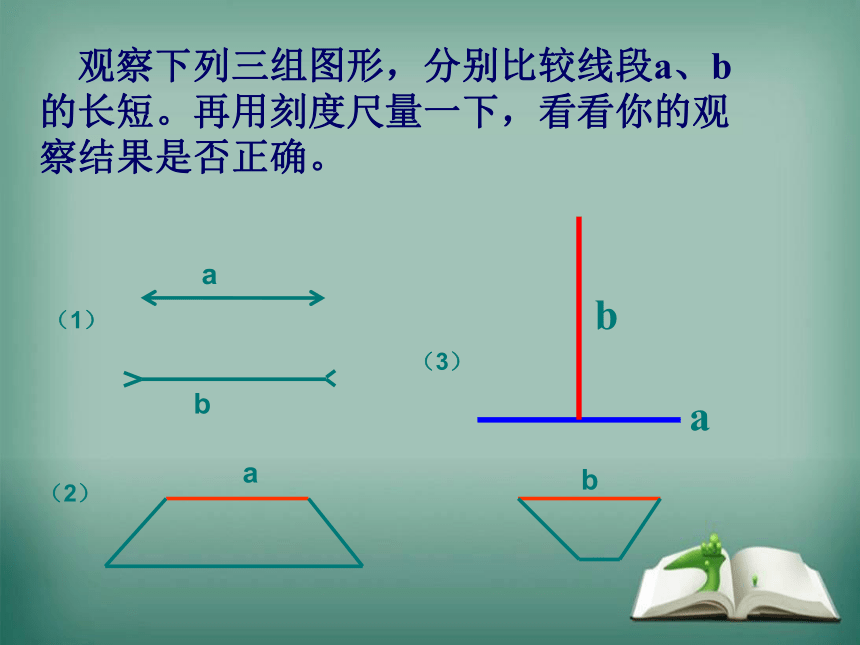
观察下列三组图形,分别比较线段a、b的长短。再用刻度尺量一下,看看你的观察结果是否正确。
1、已知线段MN,用直尺和圆规画一条线段OA,使它等于已知线段MN。
M
尺规作图注意事项:
1、作图语言要规范,要说明作图结果;
2、保留作图痕迹。
请说说你的画法
O
P
线段OA就是所求做的线段.
A
直尺只用来画线,不用来量距离;
N
a
2、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
请说说你的画法
O
P
B
线段OB就是所求做的线段c
A
尺规作图注意事项:
1、作图语言要规范,要说明作图结果;
2、保留作图痕迹。
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和。
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a ;
3、用圆规在射线AP上截取AC=b。
线段OC的长度就是等于线段a,b的长度和, 即线段OC就是所求的线段c.
O
P
A
C
线段c的长度是线段a,b的长度的和,我们就说线段c是线段a,b的和,记做c=a+b;
类似地,线段c是线段a,b的差,记做c=a-b
一看起点,二看方向,
三看落点。
已知线段a,b,(如图)用尺和圆规画一条线段c,使它的长度等于a-b。
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a;
O
P
A
3、用圆规在线段OA上截取AB=b;
B
线段OB就是所求做的线段c=a-b
一看起点,二看方向,
三看落点。
1、如图,填空:
A
B
C
D
AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
2、已知:直线l上有A、B、C三点,且线段AB=8cm,线段BC=5cm,求线段AC的长。
解:
(1)如图:
(2)如图:
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
A
B
C
A
B
C
观察下列步骤,并回答问题
(1)拿出一张白纸
(2)对折这张白纸
(3)把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
A
B
C
点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点(midpoint),可知AC=BC= AB
1
2
合作探究
反之,如图,
∵点C是线段AB的中点,
∴AC=BC= AB 或AB=2AC=2BC
1
2
线段中点的符号语言表示:
如图, ∵点C在线段AB上且AC=BC
∴点C是线段AB的中点.
练习:1、如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= _ _ BC ,BC= _ _ AD
(2)BD= _ _ AD
A
B
C
D
2
2
3
反之,
如图,∵点C是线段AB的中点,
∴AC=BC= AB
1
2
线段中点的符号语言表示:
如图,∵点C在线段AB上且AC=BC
∴点C是线段AB的中点.
A
B
C
2. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
A
D
C
B
∴AC=CB=
解:∵点C是线段AB的中点
一、学习了怎样比较线段的长短。
1、度量法:
2、叠合法:起点对齐,看终点。
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差。
三、知道线段中点的定义,会用几何符号表示线段的中点。
一看起点,二看方向,三看落点。
这节课你学到了什么?
已知线段a,b,画一条线段c,使它的长度等于3a-b
(利用直尺和圆规).
a
b
画法:
1.画射线AF.
2.用圆规在射线AF上依次截取AB=BC=CD=a.
3. 在线段AD上截取DE=b.
线段AE就是所求的线段c.
A
F
B
C
D
a
a
a
E
b
D
(或 线段AE=3a-b)
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
4.5.2 线段的长短比较
教学目标
1、掌握分别用测量与重叠来比较线段大小的方法;
2、充分理解两条线段大小比较所隐含的意义,能从“量”与“形”上进行转化;
3、线段中点的性质及其简单运算。
教学重难点
学习重点:线段大小比较的方法及其原理;
学习难点:从“数量”的角度到从“形”的角度来分析两条线段的大小比较。
复习回顾
1、
2、什么叫两点间的距离?
3、直线、线段的公理是什么?
有几个端点 向几个方向延伸 能否度量
直线
射线
线段
问题思考
(1)你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示 来比较两条线段的长短吗?讨论后派一位代表上来说说你们的想法。
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
线段的比较:
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
0
A
B
D
C
(1)如果点B在线段CD上,
记作AB
B
D
C
(2)如果点B在线段CD的延长线上, 记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
第二种方法:叠合法
注意:起点对齐,看终点
比较线段长短的两种方法:
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
(1)
a
b
(3)
(2)
a
b
a
b
观察下列三组图形,分别比较线段a、b的长短。再用刻度尺量一下,看看你的观察结果是否正确。
1、已知线段MN,用直尺和圆规画一条线段OA,使它等于已知线段MN。
M
尺规作图注意事项:
1、作图语言要规范,要说明作图结果;
2、保留作图痕迹。
请说说你的画法
O
P
线段OA就是所求做的线段.
A
直尺只用来画线,不用来量距离;
N
a
2、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
请说说你的画法
O
P
B
线段OB就是所求做的线段c
A
尺规作图注意事项:
1、作图语言要规范,要说明作图结果;
2、保留作图痕迹。
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和。
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a ;
3、用圆规在射线AP上截取AC=b。
线段OC的长度就是等于线段a,b的长度和, 即线段OC就是所求的线段c.
O
P
A
C
线段c的长度是线段a,b的长度的和,我们就说线段c是线段a,b的和,记做c=a+b;
类似地,线段c是线段a,b的差,记做c=a-b
一看起点,二看方向,
三看落点。
已知线段a,b,(如图)用尺和圆规画一条线段c,使它的长度等于a-b。
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a;
O
P
A
3、用圆规在线段OA上截取AB=b;
B
线段OB就是所求做的线段c=a-b
一看起点,二看方向,
三看落点。
1、如图,填空:
A
B
C
D
AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
2、已知:直线l上有A、B、C三点,且线段AB=8cm,线段BC=5cm,求线段AC的长。
解:
(1)如图:
(2)如图:
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
A
B
C
A
B
C
观察下列步骤,并回答问题
(1)拿出一张白纸
(2)对折这张白纸
(3)把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
A
B
C
点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点(midpoint),可知AC=BC= AB
1
2
合作探究
反之,如图,
∵点C是线段AB的中点,
∴AC=BC= AB 或AB=2AC=2BC
1
2
线段中点的符号语言表示:
如图, ∵点C在线段AB上且AC=BC
∴点C是线段AB的中点.
练习:1、如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= _ _ BC ,BC= _ _ AD
(2)BD= _ _ AD
A
B
C
D
2
2
3
反之,
如图,∵点C是线段AB的中点,
∴AC=BC= AB
1
2
线段中点的符号语言表示:
如图,∵点C在线段AB上且AC=BC
∴点C是线段AB的中点.
A
B
C
2. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
A
D
C
B
∴AC=CB=
解:∵点C是线段AB的中点
一、学习了怎样比较线段的长短。
1、度量法:
2、叠合法:起点对齐,看终点。
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差。
三、知道线段中点的定义,会用几何符号表示线段的中点。
一看起点,二看方向,三看落点。
这节课你学到了什么?
已知线段a,b,画一条线段c,使它的长度等于3a-b
(利用直尺和圆规).
a
b
画法:
1.画射线AF.
2.用圆规在射线AF上依次截取AB=BC=CD=a.
3. 在线段AD上截取DE=b.
线段AE就是所求的线段c.
A
F
B
C
D
a
a
a
E
b
D
(或 线段AE=3a-b)
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
