【精选备课】2022-2023学年华师大版数学七年级上册 5.1.1 对顶角 课件(共23张PPT)
文档属性
| 名称 | 【精选备课】2022-2023学年华师大版数学七年级上册 5.1.1 对顶角 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 11:16:37 | ||
图片预览





文档简介
(共23张PPT)
5.1.1 对顶角
教学目标
1.理解对顶角的概念,会根据概念识别对顶角。
2.掌握对顶角的性质,能根据对顶角的性质解决问题。
3. 情感态度与价值观:让学生经历在数学活动中探索对顶角性质的过程,发展学生有条理的思考与表达能力。
教学重难点
教学重点:对顶角的定义及对顶角的性质
教学难点:
1.在图形中识别对顶角;
2.能用对顶角的性质进行简单的推理和计算。
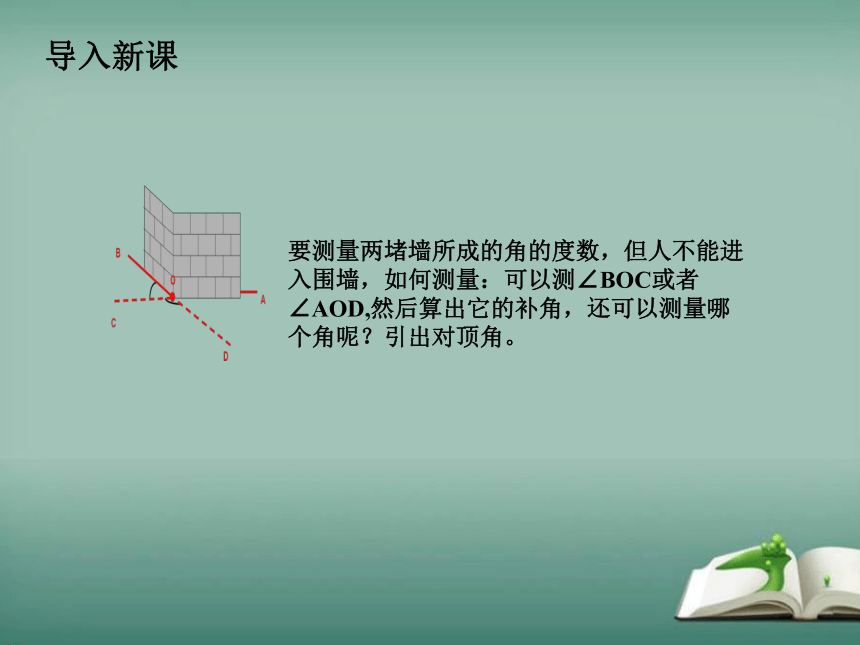
导入新课
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量:可以测∠BOC或者∠AOD,然后算出它的补角,还可以测量哪个角呢?引出对顶角。
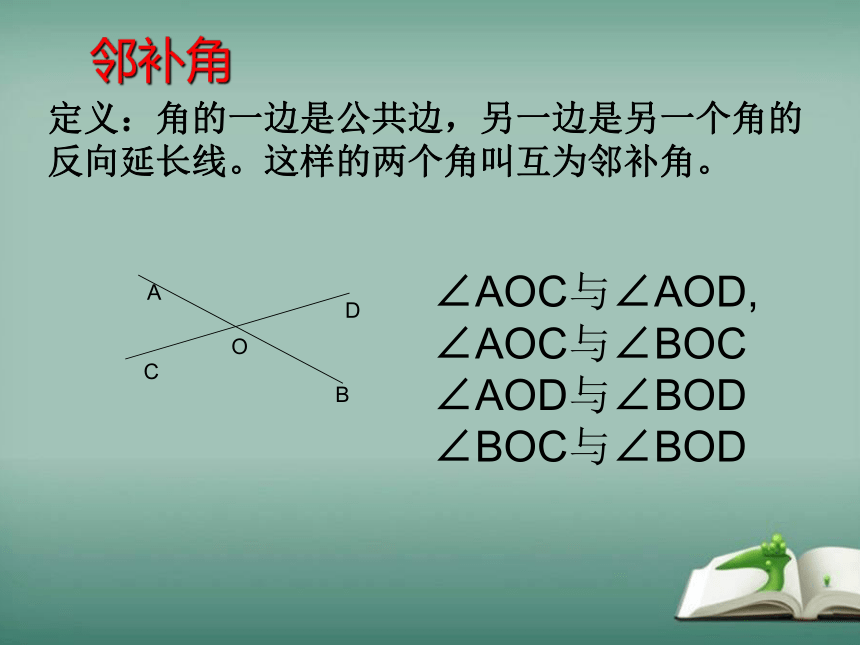
邻补角
定义:角的一边是公共边,另一边是另一个角的反向延长线。这样的两个角叫互为邻补角。
∠AOC与∠AOD, ∠AOC与∠BOC ∠AOD与∠BOD ∠BOC与∠BOD
O
D
C
B
A
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线。
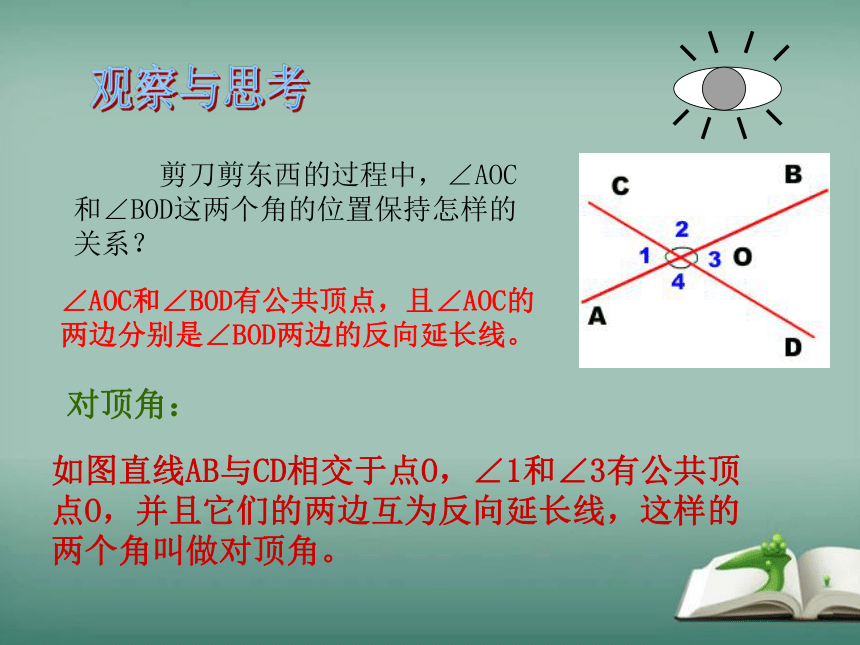
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角:
剪刀剪东西的过程中,∠AOC和∠BOD这两个角的位置保持怎样的关系?
B
A
C
D
O
1
2
3
4
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
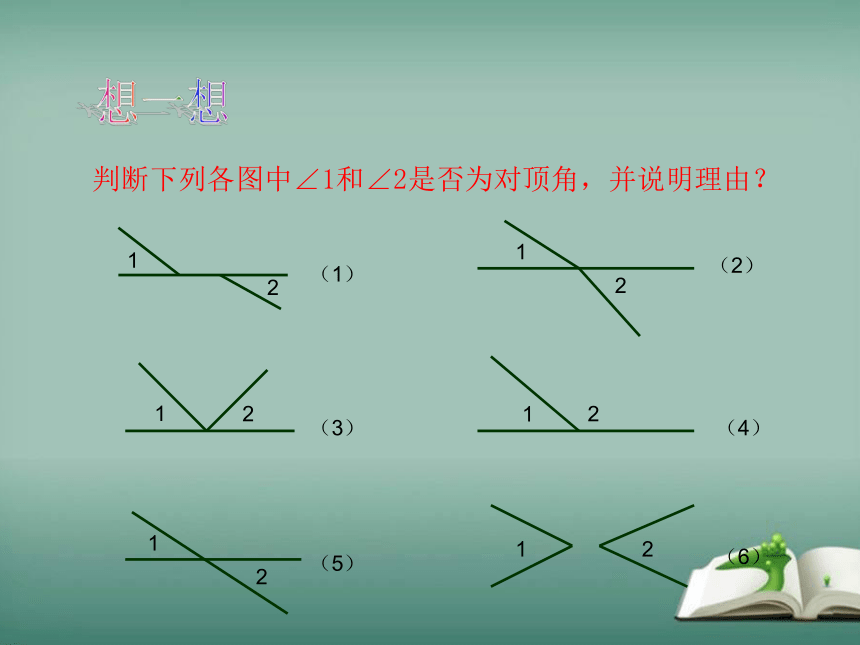
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
1
2
1
2
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
教材解读
如图所示:如果有两条直线和另一条直线相交,
(通常说:两条直线被第三条直线所截)
可以得到几个角?
八个角,形成“三线八角”图
a
b
c
直线a、b被直线c 所截
直线a、b是被截线
直线c是截线
教材解读
观察∠1与∠5的位置:
它们的位置都在两条直线AB、CD的同一方(上方),并且都在第三条直线MN的同侧.
我们把满足上面两个条件的一对角叫做同位角。
思考:
∠3与∠7是同位角吗?
还有哪几对角是同位角?
4
8
6
2
7
5
3
1
A
B
C
D
M
N
教材解读
观察∠3与∠5的位置:
它们的位置都在两条直线AB、CD之间,并且都在第三条直线MN的两侧。
我们把满足上面两个条件的一对角叫做内错角。
思考:
还有其它内错角吗?
∠4与∠6也是一对内错角。
4
8
6
2
7
5
3
1
A
B
C
D
M
N
教材解读
观察∠3与∠6的位置:
它们的位置都在两条直线AB、CD之间,并且都在第三条直线MN的同一旁.
我们把满足上面两个条件的一对角叫做同旁内角。
思考:
还有其它同旁内角吗?
∠4与∠5也是一对同旁内角。
4
8
6
2
7
5
3
1
A
B
C
D
M
N
同位角、内错角和同旁内角的结构特征
4
8
6
2
7
5
3
1
A
B
C
D
M
N
4
8
5
3
4
5
教材解读
注意:
上述三类角类似于对顶角都是成对出现的,不能说哪一个角是同位角、内错角、同旁内角.
例题解答
例3、如图,直线DE与AB、AC相交,构成8个角.
指出所有的同位角、内错角和同旁内角.
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角有:
∠1和∠8、∠2和∠5
∠4和∠7、∠3和∠6
内错角有:
∠1和∠6、∠4和∠5
同旁内角有:
∠1和∠5、∠4和∠6
解题之前要明确哪两条直线被哪条直线所截.
解:
例题解答
变式1:直线AB与DE 被AC所截,请指出其中的同位角、内错角、同旁内角?
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角有:
∠6和∠A
内错角有:
∠8和∠A
同旁内角有:
∠5和∠A
解:
例题解答
变式2:
∠A与∠8是哪两条直线被第3条直线所截的角?它们是什么关系的角?
∠A与∠5呢?
∠A与∠4呢?
技巧:找到组成这对角的几条相关的直线,两个角都有的是截线,另外两条是被截线.
E
D
C
B
A
8
7
6
5
4
3
2
1
动脑筋
如图所示,假设直线AB、CD被MN所截,有一对同位角相等,比如说∠1=∠5.
5
8
6
7
4
1
2
3
A
B
C
D
M
N
(1)∠3与∠1是什么角?
∠7与∠5是什么角?
同位角∠3与∠7相等吗?
(2)内错角∠3与∠5相等吗?
(3)∠4与∠1互补吗?
同旁内角∠4与∠5互补吗?
教材解读
应用“对顶角相等”、“等量代换”及等式的基本性质可以得出:
(1)两直线被第三条直线所截,如果有一对同位角相等,那么其它几对同位角也相等,并且内错角相等,同旁内角互补。
类似地还可以得出:
(2)两直线被第三条直线所截,如果有一对内错角相等,那么另一对内错角也相等,并且同位角相等,同旁内角互补。
(3)两直线被第三条直线所截,如果有一对同旁内角互补,那么另一对同旁内角也互补,并且同位角相等,内错角相等。
课堂练习
1、如图:
(1)直线AB、CD 被直线 AC 所截,所产生的内错角是____________。
(2)直线AD、BC 被直线 DC 所截,产生了___角,它们是_____________。
D
C
B
A
课堂练习
2、(1)如果把图看成是直线AB、EF被直线CD所截,那么∠1与∠2是一对什么角?∠3与∠4呢? ∠2与∠4呢?
2
5
3
4
1
E
F
A
B
D
C
(2)如果把图看成是直线CD、EF被直线AB所截,那么∠1与∠5是一对什么角?∠4与∠5呢?
(3)哪两条直线被哪一条所截,∠2与∠5是同位角
课堂练习
3、如图:直线DE交∠ABC的 边BA于点 F. 如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。 请说明理由。
4
3
2
1
F
E
D
C
B
A
本课小结
1、同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握它们的位置特征。
2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截,分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。
5.1.1 对顶角
教学目标
1.理解对顶角的概念,会根据概念识别对顶角。
2.掌握对顶角的性质,能根据对顶角的性质解决问题。
3. 情感态度与价值观:让学生经历在数学活动中探索对顶角性质的过程,发展学生有条理的思考与表达能力。
教学重难点
教学重点:对顶角的定义及对顶角的性质
教学难点:
1.在图形中识别对顶角;
2.能用对顶角的性质进行简单的推理和计算。
导入新课
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量:可以测∠BOC或者∠AOD,然后算出它的补角,还可以测量哪个角呢?引出对顶角。
邻补角
定义:角的一边是公共边,另一边是另一个角的反向延长线。这样的两个角叫互为邻补角。
∠AOC与∠AOD, ∠AOC与∠BOC ∠AOD与∠BOD ∠BOC与∠BOD
O
D
C
B
A
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线。
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角:
剪刀剪东西的过程中,∠AOC和∠BOD这两个角的位置保持怎样的关系?
B
A
C
D
O
1
2
3
4
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
1
2
1
2
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
教材解读
如图所示:如果有两条直线和另一条直线相交,
(通常说:两条直线被第三条直线所截)
可以得到几个角?
八个角,形成“三线八角”图
a
b
c
直线a、b被直线c 所截
直线a、b是被截线
直线c是截线
教材解读
观察∠1与∠5的位置:
它们的位置都在两条直线AB、CD的同一方(上方),并且都在第三条直线MN的同侧.
我们把满足上面两个条件的一对角叫做同位角。
思考:
∠3与∠7是同位角吗?
还有哪几对角是同位角?
4
8
6
2
7
5
3
1
A
B
C
D
M
N
教材解读
观察∠3与∠5的位置:
它们的位置都在两条直线AB、CD之间,并且都在第三条直线MN的两侧。
我们把满足上面两个条件的一对角叫做内错角。
思考:
还有其它内错角吗?
∠4与∠6也是一对内错角。
4
8
6
2
7
5
3
1
A
B
C
D
M
N
教材解读
观察∠3与∠6的位置:
它们的位置都在两条直线AB、CD之间,并且都在第三条直线MN的同一旁.
我们把满足上面两个条件的一对角叫做同旁内角。
思考:
还有其它同旁内角吗?
∠4与∠5也是一对同旁内角。
4
8
6
2
7
5
3
1
A
B
C
D
M
N
同位角、内错角和同旁内角的结构特征
4
8
6
2
7
5
3
1
A
B
C
D
M
N
4
8
5
3
4
5
教材解读
注意:
上述三类角类似于对顶角都是成对出现的,不能说哪一个角是同位角、内错角、同旁内角.
例题解答
例3、如图,直线DE与AB、AC相交,构成8个角.
指出所有的同位角、内错角和同旁内角.
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角有:
∠1和∠8、∠2和∠5
∠4和∠7、∠3和∠6
内错角有:
∠1和∠6、∠4和∠5
同旁内角有:
∠1和∠5、∠4和∠6
解题之前要明确哪两条直线被哪条直线所截.
解:
例题解答
变式1:直线AB与DE 被AC所截,请指出其中的同位角、内错角、同旁内角?
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角有:
∠6和∠A
内错角有:
∠8和∠A
同旁内角有:
∠5和∠A
解:
例题解答
变式2:
∠A与∠8是哪两条直线被第3条直线所截的角?它们是什么关系的角?
∠A与∠5呢?
∠A与∠4呢?
技巧:找到组成这对角的几条相关的直线,两个角都有的是截线,另外两条是被截线.
E
D
C
B
A
8
7
6
5
4
3
2
1
动脑筋
如图所示,假设直线AB、CD被MN所截,有一对同位角相等,比如说∠1=∠5.
5
8
6
7
4
1
2
3
A
B
C
D
M
N
(1)∠3与∠1是什么角?
∠7与∠5是什么角?
同位角∠3与∠7相等吗?
(2)内错角∠3与∠5相等吗?
(3)∠4与∠1互补吗?
同旁内角∠4与∠5互补吗?
教材解读
应用“对顶角相等”、“等量代换”及等式的基本性质可以得出:
(1)两直线被第三条直线所截,如果有一对同位角相等,那么其它几对同位角也相等,并且内错角相等,同旁内角互补。
类似地还可以得出:
(2)两直线被第三条直线所截,如果有一对内错角相等,那么另一对内错角也相等,并且同位角相等,同旁内角互补。
(3)两直线被第三条直线所截,如果有一对同旁内角互补,那么另一对同旁内角也互补,并且同位角相等,内错角相等。
课堂练习
1、如图:
(1)直线AB、CD 被直线 AC 所截,所产生的内错角是____________。
(2)直线AD、BC 被直线 DC 所截,产生了___角,它们是_____________。
D
C
B
A
课堂练习
2、(1)如果把图看成是直线AB、EF被直线CD所截,那么∠1与∠2是一对什么角?∠3与∠4呢? ∠2与∠4呢?
2
5
3
4
1
E
F
A
B
D
C
(2)如果把图看成是直线CD、EF被直线AB所截,那么∠1与∠5是一对什么角?∠4与∠5呢?
(3)哪两条直线被哪一条所截,∠2与∠5是同位角
课堂练习
3、如图:直线DE交∠ABC的 边BA于点 F. 如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。 请说明理由。
4
3
2
1
F
E
D
C
B
A
本课小结
1、同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握它们的位置特征。
2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截,分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
