【精选备课】2022-2023学年华师大版数学七年级上册 5.1.2 垂线 课件(共20张PPT)
文档属性
| 名称 | 【精选备课】2022-2023学年华师大版数学七年级上册 5.1.2 垂线 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 22:46:54 | ||
图片预览








文档简介
(共20张PPT)
5.1.2 垂线
教学目标
1.理解垂线概念,知道互相垂直的两条直线夹角是90°.
2.知道过一点有且只有一条直线与已知直线垂直,会过一点画一条直线的垂线.
3.从不同角度寻求垂线的画法,获得成功体验.
教学重难点
教学重点:
如何确定点到直线的距离以及垂直的公理.
教学难点:
垂线的判断和性质的理解运用及垂线的画法.
引入新课
思考:
1.什么样的两个角互为邻补角?什么样的两个角互为对顶角?对顶角有什么性质?
2.如图所示,直线AB、CD交于点O
(1)如果∠1=40°,则其他三个角各为多少度?
(2)如果∠1=90°,则其他三个角各为多少度?
今天我们进一步研究两条直线相交的特殊情况:垂直.
新知探究
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.它们会出现四个角相等的情况吗?每个角多少度?
两条直线相交出现两对对顶角,如果两条直线转动到所形成的四个角都相等的时候(直角),它们的位置关系咱们能不能给它起个名字显示它的特殊性呢?
总结:当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角,此时,称这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.交点O叫做垂足.
垂直用符号 “⊥”来表示,读作“垂直于”
如图表示为:AB⊥CD,垂足为O.
用几何语言表示为:∵∠AOC=90°(∠BOC=∠AOD=∠BOD=90°)
∴AB⊥CD
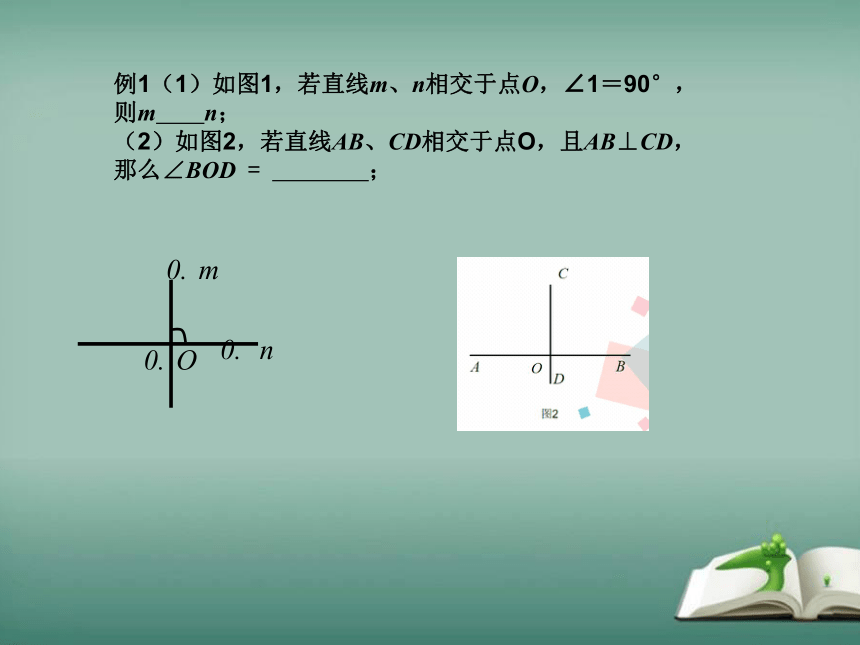
例1(1)如图1,若直线m、n相交于点O,∠1=90°,则m n;
(2)如图2,若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD = ;
O
m
n
线的性质:过一点有且只有一条直线与已知直线垂直.(学生概括教师补充)
注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
练习1.过点P 向线段AB 所在直线引垂线,正确的是( )
例2 如图所示的各个三角形中,分别过点C画直线AB的垂线.
如图所示,点A是直线l外一点,AD与直线l垂直,垂足为D,点A与直线l上各点(B、C、D、E.....)的距离长短不一.
量一量哪条线段最短呢?
练习2.下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
课堂检测
1.点到直线的距离是指( )
A.从直线外一点到这条直线的垂线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线段的长 D.从直线外一点到这条直线的垂线的长
C
2.下列图形中,线段AD的长表示点A到
直线BC距离的是( )
A
B
C
D
D
3.如图,∠ACB=90°,CD⊥AB,垂足为D,那么点B到AC的距离是线段 的长度,点A到BC的距离是线段 的长度,点C到AB的距离是线段 的长度,点A与点C的距离是
线段 的长度。
BC
AC
CD
AC
4. 如图,CD⊥AD,BE⊥AC,AF⊥CF,CD=2cm,BE=1.5cm,AF=4cm,分别求点A、B、C到直线BC、AC、AB的距离.
5.如图,运动会上,小明以直线AB为起跳线,两脚落在点P处,甲乙两名同学测得小明的跳远成绩分别为PA=5.5米,PB=5.1米,则小明的真实成绩为 米.
如图,画出
1.村庄A到货场B怎样走最近?为什么?
2.货场B到铁道怎样走最近?为什么?
C
A
B
回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗?
谢 谢
5.1.2 垂线
教学目标
1.理解垂线概念,知道互相垂直的两条直线夹角是90°.
2.知道过一点有且只有一条直线与已知直线垂直,会过一点画一条直线的垂线.
3.从不同角度寻求垂线的画法,获得成功体验.
教学重难点
教学重点:
如何确定点到直线的距离以及垂直的公理.
教学难点:
垂线的判断和性质的理解运用及垂线的画法.
引入新课
思考:
1.什么样的两个角互为邻补角?什么样的两个角互为对顶角?对顶角有什么性质?
2.如图所示,直线AB、CD交于点O
(1)如果∠1=40°,则其他三个角各为多少度?
(2)如果∠1=90°,则其他三个角各为多少度?
今天我们进一步研究两条直线相交的特殊情况:垂直.
新知探究
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.它们会出现四个角相等的情况吗?每个角多少度?
两条直线相交出现两对对顶角,如果两条直线转动到所形成的四个角都相等的时候(直角),它们的位置关系咱们能不能给它起个名字显示它的特殊性呢?
总结:当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角,此时,称这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.交点O叫做垂足.
垂直用符号 “⊥”来表示,读作“垂直于”
如图表示为:AB⊥CD,垂足为O.
用几何语言表示为:∵∠AOC=90°(∠BOC=∠AOD=∠BOD=90°)
∴AB⊥CD
例1(1)如图1,若直线m、n相交于点O,∠1=90°,则m n;
(2)如图2,若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD = ;
O
m
n
线的性质:过一点有且只有一条直线与已知直线垂直.(学生概括教师补充)
注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
练习1.过点P 向线段AB 所在直线引垂线,正确的是( )
例2 如图所示的各个三角形中,分别过点C画直线AB的垂线.
如图所示,点A是直线l外一点,AD与直线l垂直,垂足为D,点A与直线l上各点(B、C、D、E.....)的距离长短不一.
量一量哪条线段最短呢?
练习2.下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
课堂检测
1.点到直线的距离是指( )
A.从直线外一点到这条直线的垂线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线段的长 D.从直线外一点到这条直线的垂线的长
C
2.下列图形中,线段AD的长表示点A到
直线BC距离的是( )
A
B
C
D
D
3.如图,∠ACB=90°,CD⊥AB,垂足为D,那么点B到AC的距离是线段 的长度,点A到BC的距离是线段 的长度,点C到AB的距离是线段 的长度,点A与点C的距离是
线段 的长度。
BC
AC
CD
AC
4. 如图,CD⊥AD,BE⊥AC,AF⊥CF,CD=2cm,BE=1.5cm,AF=4cm,分别求点A、B、C到直线BC、AC、AB的距离.
5.如图,运动会上,小明以直线AB为起跳线,两脚落在点P处,甲乙两名同学测得小明的跳远成绩分别为PA=5.5米,PB=5.1米,则小明的真实成绩为 米.
如图,画出
1.村庄A到货场B怎样走最近?为什么?
2.货场B到铁道怎样走最近?为什么?
C
A
B
回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗?
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
