高中数学人教A版2019必修第二册 8.3.2《棱柱、棱锥、棱台的表面积和体积》教学设计(表格式)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 8.3.2《棱柱、棱锥、棱台的表面积和体积》教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 240.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 14:31:16 | ||
图片预览


文档简介
《棱柱、棱锥、棱台的表面积和体积》教学设计
教学设计
教学环节 教学内容 师生互动 设计意图
创设情境 在初中我们学习了特殊的棱柱—正方体、长方体的体积公式及其表面积的求法,那么对于一个更一般的棱柱或棱锥、棱台,它们的体积及表面积又如何来计算呢? 学生先思考讨论,然后回答,教师补充完善. 创设问题情境,激发学生的学习兴趣.
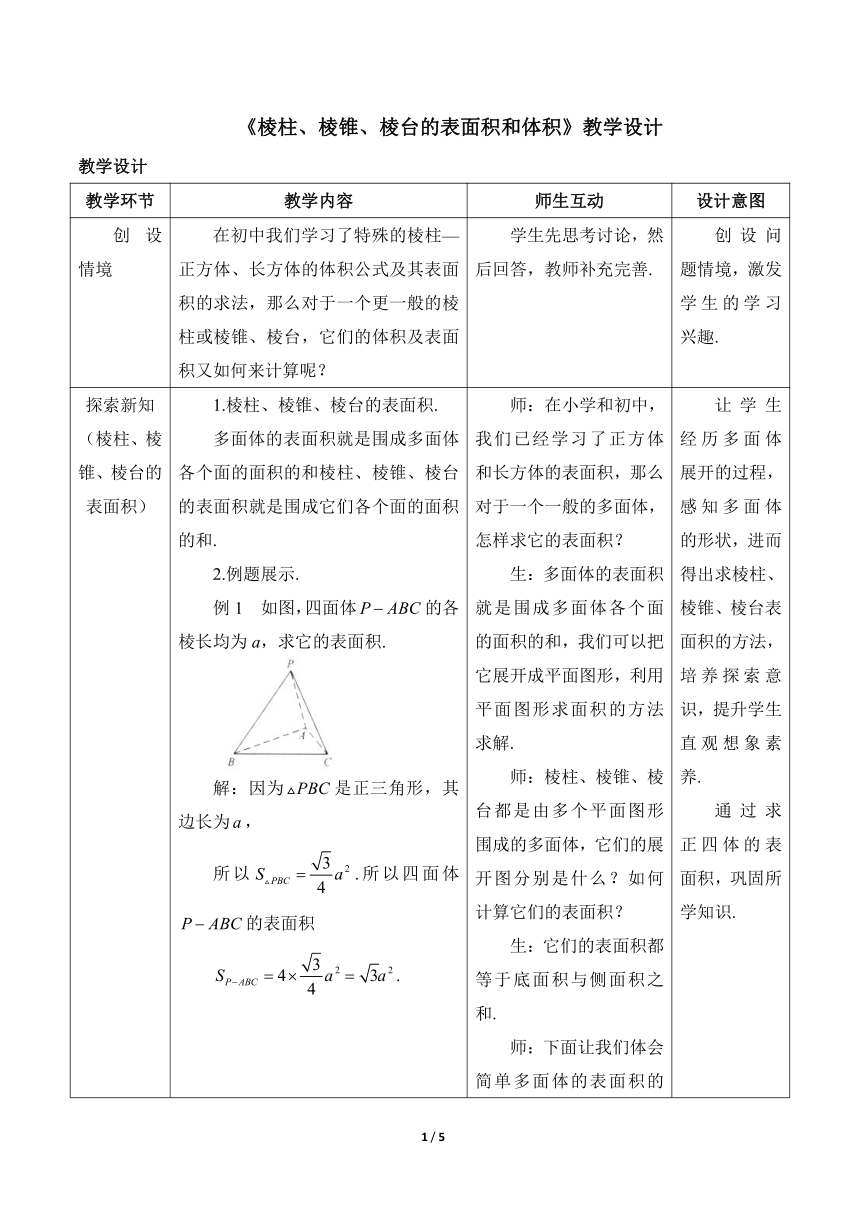
探索新知(棱柱、棱锥、棱台的表面积) 1.棱柱、棱锥、棱台的表面积.多面体的表面积就是围成多面体各个面的面积的和棱柱、棱锥、棱台的表面积就是围成它们各个面的面积的和.2.例题展示.例1 如图,四面体的各棱长均为a,求它的表面积.解:因为是正三角形,其边长为,所以.所以四面体的表面积. 师:在小学和初中,我们已经学习了正方体和长方体的表面积,那么对于一个一般的多面体,怎样求它的表面积?生:多面体的表面积就是围成多面体各个面的面积的和,我们可以把它展开成平面图形,利用平面图形求面积的方法求解.师:棱柱、棱锥、棱台都是由多个平面图形围成的多面体,它们的展开图分别是什么?如何计算它们的表面积?生:它们的表面积都等于底面积与侧面积之和.师:下面让我们体会简单多面体的表面积的计算.教师投影出例题,学生阅读,分析题目,整理思路.生:由于四面体的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.教师板书解答过程. 让学生经历多面体展开的过程,感知多面体的形状,进而得出求棱柱、棱锥、棱台表面积的方法,培养探索意识,提升学生直观想象素养.通过求正四体的表面积,巩固所学知识.
探索新知(棱柱、棱锥、棱台的体积) 1.棱柱、棱锥、棱台的体积.棱柱的体积(S是棱柱的底面积,h为棱柱的高);棱锥的体积(S是棱锥的底面积,h为棱锥的高);棱台的体积(,S分别为棱台和上、下底面面积,h为棱台的高).说明:棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间距离.2.棱柱、棱锥、棱台的体积公式之间的关系.3.例题展示例2 如图,一个漏斗的上面部分是个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到)?解:由题意知 .所以这个漏斗的容积. 师:我们已经学习了特殊的棱柱—正方体、长方体的体积公式,它们分别是什么?生:(a是正方体的棱长),(分别是长方体的长、宽、高).师:一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积.如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积.师:棱台的结构特征是什么?生:棱台是用一个平行于棱锥底面的平面去截棱锥,底面与截面之间那部分多面体.师:棱台的体积可以怎样求?生:棱台的体积应该等于两个棱锥的体积差.师:利用这个原理我们可以得到棱台的体积公式,其中,S分别为棱台的上、下底面面积,h为棱台的高.师:现在大家讨论思考一下棱台的体积公式与棱柱、棱锥的体积公式之间有什么关系.生:令,得到棱锥的体积公式,令,得到棱柱的体积公式.师:漏斗表示的几何体的结构特征是什么?你准备怎样计算它的容积?生:漏斗表示的几何体是一个组合体,在一个长方体下方放置一个倒放的等底的四棱锥,因此它的容积等于长方体的体积加上四棱锥的体积.学生分析,教师板书解答过程.师:求组合体的体积时,要注意组合体的结构特征,避免重叠和交叉等. 棱柱、棱锥、棱台的体积公式只要求了解,故采用讲授式效率会更高.因为棱台的体积公式的推导需要用到后面的知识,故此处不予证明,只需要学生了解公式及公式的推导思路.培养探索意识,加深对棱柱、棱锥、棱台的体积公式之间关系的理解.通过例题展示,强调空间组合体的体积计算的关键在于弄清它的结构特征.
归纳总结 1.棱柱、棱锥、棱台的表面积.2.棱柱、棱锥、棱台的体积. 学生归纳,教师补充完善. 前后联系,加强知识的系统性.
课后作业 教材第116页练习第1,3题. 学生独立完成. 巩固知识,提升能力.
板书设计
8.3.1棱柱、棱锥、棱台的表面积和体积1.棱柱、棱锥、棱台的表面积例12.棱柱、棱锥、棱台的体积例2小结1.棱柱、棱锥、棱台的表面积2.棱柱、棱锥、棱台的体积作业教材第116页练习第1,3题
1 / 4
教学设计
教学环节 教学内容 师生互动 设计意图
创设情境 在初中我们学习了特殊的棱柱—正方体、长方体的体积公式及其表面积的求法,那么对于一个更一般的棱柱或棱锥、棱台,它们的体积及表面积又如何来计算呢? 学生先思考讨论,然后回答,教师补充完善. 创设问题情境,激发学生的学习兴趣.
探索新知(棱柱、棱锥、棱台的表面积) 1.棱柱、棱锥、棱台的表面积.多面体的表面积就是围成多面体各个面的面积的和棱柱、棱锥、棱台的表面积就是围成它们各个面的面积的和.2.例题展示.例1 如图,四面体的各棱长均为a,求它的表面积.解:因为是正三角形,其边长为,所以.所以四面体的表面积. 师:在小学和初中,我们已经学习了正方体和长方体的表面积,那么对于一个一般的多面体,怎样求它的表面积?生:多面体的表面积就是围成多面体各个面的面积的和,我们可以把它展开成平面图形,利用平面图形求面积的方法求解.师:棱柱、棱锥、棱台都是由多个平面图形围成的多面体,它们的展开图分别是什么?如何计算它们的表面积?生:它们的表面积都等于底面积与侧面积之和.师:下面让我们体会简单多面体的表面积的计算.教师投影出例题,学生阅读,分析题目,整理思路.生:由于四面体的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.教师板书解答过程. 让学生经历多面体展开的过程,感知多面体的形状,进而得出求棱柱、棱锥、棱台表面积的方法,培养探索意识,提升学生直观想象素养.通过求正四体的表面积,巩固所学知识.
探索新知(棱柱、棱锥、棱台的体积) 1.棱柱、棱锥、棱台的体积.棱柱的体积(S是棱柱的底面积,h为棱柱的高);棱锥的体积(S是棱锥的底面积,h为棱锥的高);棱台的体积(,S分别为棱台和上、下底面面积,h为棱台的高).说明:棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间距离.2.棱柱、棱锥、棱台的体积公式之间的关系.3.例题展示例2 如图,一个漏斗的上面部分是个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到)?解:由题意知 .所以这个漏斗的容积. 师:我们已经学习了特殊的棱柱—正方体、长方体的体积公式,它们分别是什么?生:(a是正方体的棱长),(分别是长方体的长、宽、高).师:一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积.如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积.师:棱台的结构特征是什么?生:棱台是用一个平行于棱锥底面的平面去截棱锥,底面与截面之间那部分多面体.师:棱台的体积可以怎样求?生:棱台的体积应该等于两个棱锥的体积差.师:利用这个原理我们可以得到棱台的体积公式,其中,S分别为棱台的上、下底面面积,h为棱台的高.师:现在大家讨论思考一下棱台的体积公式与棱柱、棱锥的体积公式之间有什么关系.生:令,得到棱锥的体积公式,令,得到棱柱的体积公式.师:漏斗表示的几何体的结构特征是什么?你准备怎样计算它的容积?生:漏斗表示的几何体是一个组合体,在一个长方体下方放置一个倒放的等底的四棱锥,因此它的容积等于长方体的体积加上四棱锥的体积.学生分析,教师板书解答过程.师:求组合体的体积时,要注意组合体的结构特征,避免重叠和交叉等. 棱柱、棱锥、棱台的体积公式只要求了解,故采用讲授式效率会更高.因为棱台的体积公式的推导需要用到后面的知识,故此处不予证明,只需要学生了解公式及公式的推导思路.培养探索意识,加深对棱柱、棱锥、棱台的体积公式之间关系的理解.通过例题展示,强调空间组合体的体积计算的关键在于弄清它的结构特征.
归纳总结 1.棱柱、棱锥、棱台的表面积.2.棱柱、棱锥、棱台的体积. 学生归纳,教师补充完善. 前后联系,加强知识的系统性.
课后作业 教材第116页练习第1,3题. 学生独立完成. 巩固知识,提升能力.
板书设计
8.3.1棱柱、棱锥、棱台的表面积和体积1.棱柱、棱锥、棱台的表面积例12.棱柱、棱锥、棱台的体积例2小结1.棱柱、棱锥、棱台的表面积2.棱柱、棱锥、棱台的体积作业教材第116页练习第1,3题
1 / 4
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
