第一章特殊的四边形检测题（附答案）

特殊四边形检测题
一、选择题（每小题3分，共36分）
1.下列条件中，能判定四边形是平行四边形的是（ ）
A.一组对角相等 B.对角线互相平分
C.一组对边相等 D.对角线互相垂直
2.如图，是我国古代数学家赵爽所著的《勾股圆方图注》中所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是（ ）
A.它是轴对称图形，但不是中心对称图形
B.它是中心对称图形，但不是轴对称图形
C.它既是轴对称图形，又是中心对称图形
D.它既不是轴对称图形，又不是中心对称图形
3.有下列四个命题:
(1)两条对角线互相平分的四边形是平行四边形；
(2)两条对角线相等的四边形是菱形；
(3)两条对角线互相垂直的四边形是正方形；
(4)两条对角线相等且互相垂直的四边形是正方形.其中正确的个数为( )
A.4 B.3 C.2 D.1
4.下列说法中，正确的是（ ）
A.等腰梯形既是中心对称图形又是轴对称图形
B.正方形的对角线互相垂直平分且相等
C.矩形是轴对称图形且有四条对称轴
D.菱形的对角线相等
5.已知三角形的三个顶点坐标，求三角形面积通常有以下三种方法：
方法1：直接法：计算三角形一边的长，并求出该边上的高；
方法2：补形法：将三角形面积转化成若干个特殊的四边形和三角形的面积的和与差；
方法3：分割法：选择一条恰当的直线，将三角形分割成两个便于计算面积的三角形．
现给出三点坐标：（-1，4），（2，2），（4，-1），请你选择一种方法计算
△的面积，你的答案是（ ）
A. B. C. D.
6.如图，在菱形中，，∠，则对角线等于（ ）
A.20 B.15
C.10 D.5
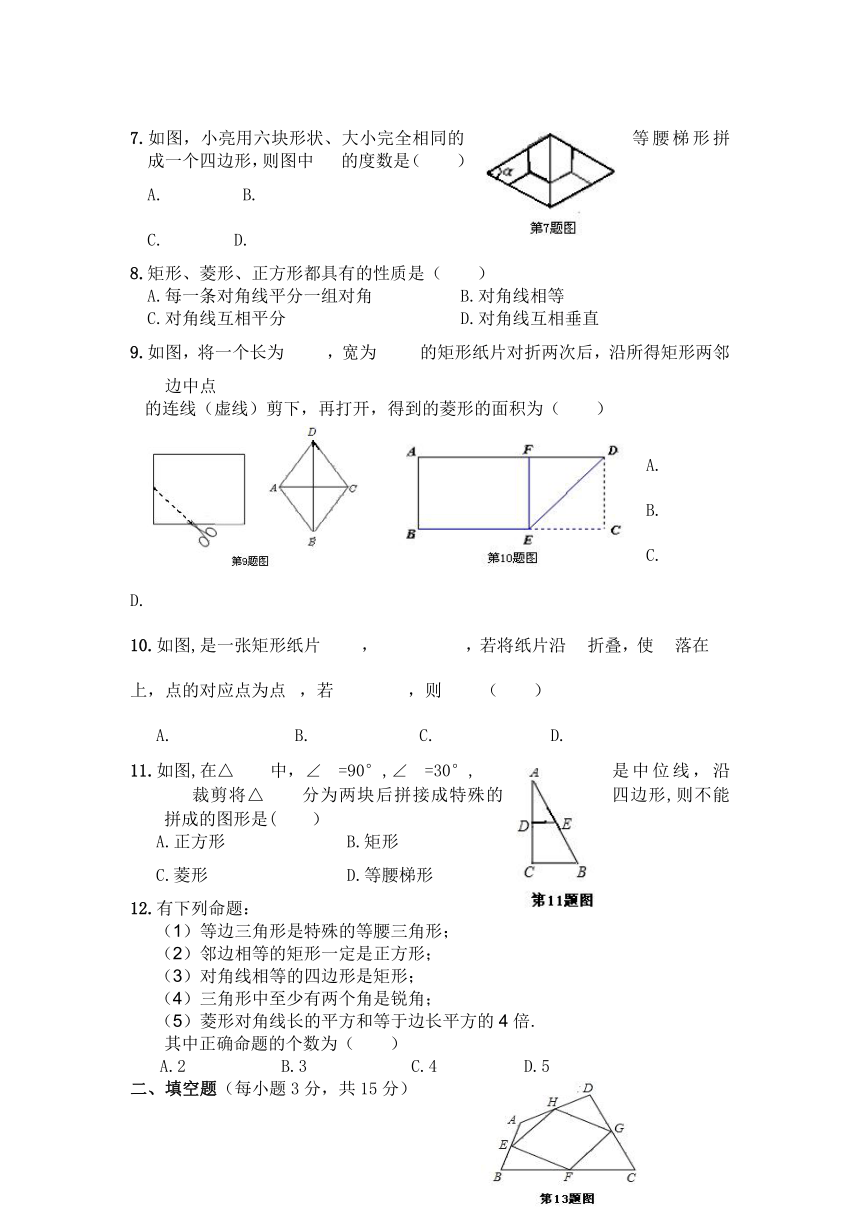
7.如图，小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形，则图中的度数是（ ）
A. B.
C. D.
8.矩形、菱形、正方形都具有的性质是（　　）
A.每一条对角线平分一组对角 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
9.如图，将一个长为，宽为 的矩形纸片对折两次后，沿所得矩形两邻边中点
的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）
A. B. C. D.
10.如图,是一张矩形纸片， ，若将纸片沿折叠，使落在上，点的对应点为点，若，则（　　）
A. B. C. D.
11.如图,在△中，∠=90°,∠=30°,是中位线，沿裁剪将△分为两块后拼接成特殊的四边形,则不能拼成的图形是( ）
A.正方形 B.矩形
C.菱形 D.等腰梯形
12.有下列命题：
（1）等边三角形是特殊的等腰三角形；
（2）邻边相等的矩形一定是正方形；
（3）对角线相等的四边形是矩形；
（4）三角形中至少有两个角是锐角；
（5）菱形对角线长的平方和等于边长平方的4倍.
其中正确命题的个数为（　　）
A.2 B.3 C.4 D.5
二、填空题（每小题3分，共15分）
13.如图所示，在四边形中，、、、分别是、、、的中点，请添加一个与四边形对角线有关的条件为 ，使四边形是特殊的平行四边形，为 形.
14.已知在四边形ABCD中，，若添加一个条件即可判定该四边形是正方形，则这个条件可以是__________．
15.如图，在菱形中，对角线相交于点，若再补充一个条件能使菱形成为正方形，
则这个条件是 （只填一个条件即可）．
16.如图，在等腰梯形中，∥，=，，∠，，则上底的长是_______.
17. 如图，矩形 的对角线 ，，则图中五个小矩形的周长之和为_______ ．
答案卷
一、选择题（每小题3分，共36分）
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题（每小题3分，共15分）
13 ._____________ __________ 14._________________
15._________________________ 16._________________
17._________________________
三、解答题（共69分）
18. (9分)如图，是△的一条角平分线，DK∥AB交BC于点E，且DK=BC，连接BK，CK，得到四边形DCKB，请判断四边形DCKB是哪种特殊四边形，并说明理由．
19.（9分）如图，在四边形中，∥， ，,求四边形 的周长．
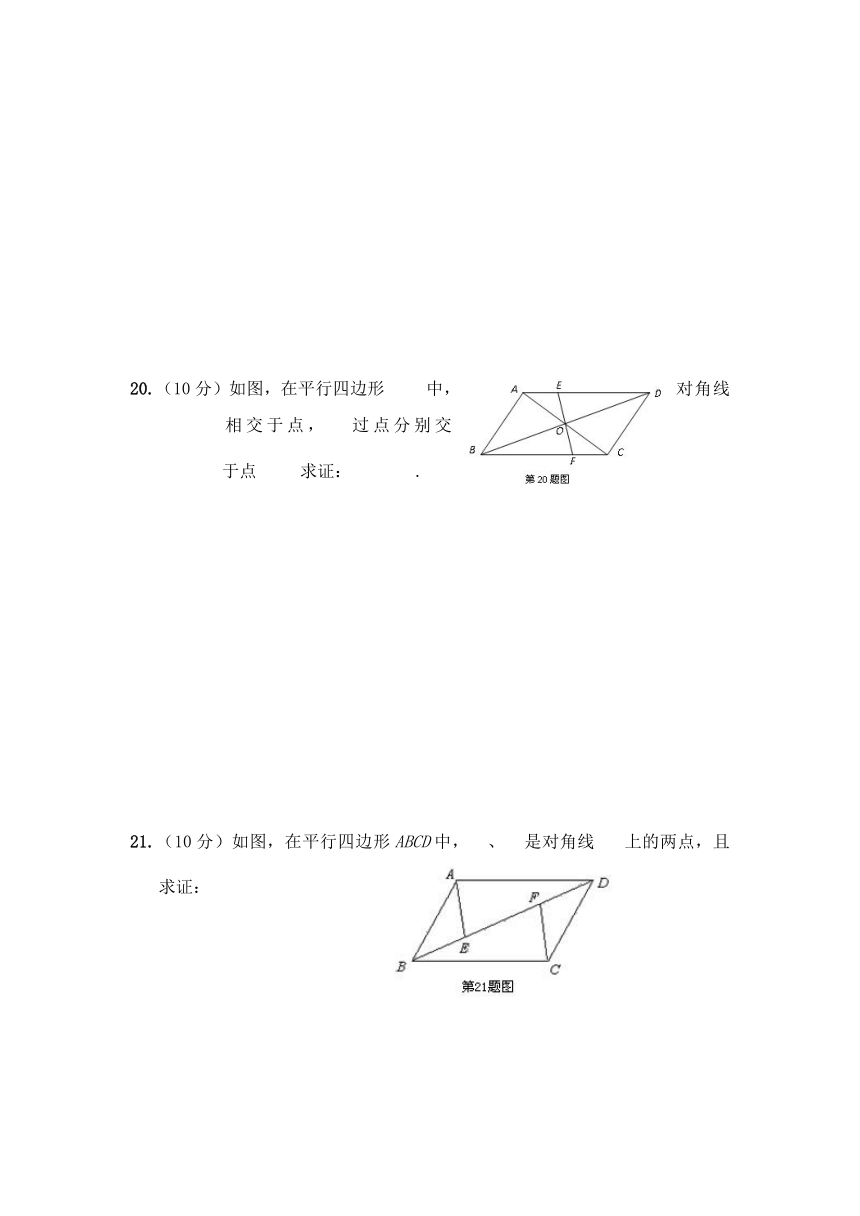
20.（10分）如图，在平行四边形中，对角线相交于点，过点分别交于点求证：.
21.（10分）如图，在平行四边形ABCD中，、是对角线上的两点，且
求证：
22.（10分）如图，在△和△中，与交于点．
（1）求证：△≌△；
（2）过点作∥，过点作∥，与交于点，
试判断线段与的数量关系，并证明你的结论．
23.（10分） 如图，在梯形中，，过对角线的中点作，分别交边于点，连接．
（1）求证：四边形是菱形；
（2）若， ，求四边形的面积．
24.（11分）如图，点是正方形内一点，△是等边三角形，连接，延长交边于点．
（1）求证：△≌△；
（2）求∠的度数．
特殊四边形检测题参考答案
1.B 解析：由平行四边形的判定定理知选项B正确.
2.B 解析：根据轴对称图形、中心对称图形的定义解题.
3.D 解析：只有（1）正确，（2）（3）（4）错误.
4.B 解析：A.等腰梯形是轴对称图形，但不是中心对称图形；C.矩形是轴对称图形，但对称轴有两条；D.菱形的对角线互相垂直，但不一定相等.
5.B 解析：选择方法2．过点A向轴引垂线，过点B向轴引垂线，两垂线相交于点D，连接CD，则△ABC的面积=，直接计算即可．即
△ABC的面积.故选B．
点拨：补形法是常用的方法，关键是得到若干个特殊的四边形和三角形的面积的和与差．易错点在于准确找到各三角形相应的底与高．
6.D 解析：在菱形中，由∠=，得 ∠.又∵ ，
∴ △是等边三角形，∴ .
7.A 解析：观察图形，在等腰梯形的一个上底角顶点处有三个上底角，因而等腰梯形上底角等于，所以.
8.C 解析：根据矩形、菱形、正方形的性质解题.
9.A 解析：由题意知 4 ， 5 ，∴ .
10.A 解析：由折叠的性质知，四边形为正方形，
∴ .
11. A 解析：首先拼出各种类型的图形（如图），再根据特殊四边形的判定判断是不是正方形、菱形、等腰梯形、矩形即可．
选项A，不论如何放置都不能判断所得的四边形是正方形，故本选项符合选择条件.
选项B，如图（1），所得的四边形是矩形，故本选项不符合选择条件.
选项C，如图（2），所得的四边形是平行四边形，
因为垂直平分，所以.又∠=60°，所以△是等边三角形，
所以，即平行四边形是菱形，故本选项不符合选择条件.
选项D，如图（3），所得的四边形是等腰梯形，故本选项不符合选择条件.故选A．
点拨：本题主要考查了三角形的中位线定理、平行四边形的性质和判定、菱形的判定、正方形的判定、等腰梯形的判定等知识点，解此题的关键是正确拼出各种类型的图形．
12. C 解析：分别根据等腰三角形的性质、正方形的判定、矩形的判定、三角形内角和定理以及菱形的性质判断即可得出答案．
（1）等边三角形是特殊的等腰三角形，根据等腰三角形的性质得出此命题正确.
（2）邻边相等的矩形一定是正方形，根据正方形的判定得出此命题正确.
（3）对角线相等的四边形也可能是等腰梯形，故此命题错误.
（4）三角形中至少有两个角是锐角，根据三角形内角和定理得出 此命题正确.
（5）如图所示，∵菱形的对角线互相垂直，∴ .
∵ ，
∴ 菱形对角线长的平方和等于边长平方的4倍，故此命题正确.
因此正确的有4个，故选C．
13.对角线相等 菱 解析：如图，连接，
∵ 分别是的中点，
∴ ,，
∴，∴ 四边形是平行四边形.
∵，∴ ，
∴ 平行四边形是菱形.
点拨：本题主要考查对三角形的中位线定理、平行四边形的判定、菱形的判定等知识点的理解和掌握，能求出四边形是平行四边形是解此题的关键．
14.
15.或或（答案不唯一）
16.2 解析：∠.
在等腰梯形中，∠∠，
∵ ∠∠∠
又∵ ∥∴ ∠∠∠.
∴ .
17.28 解析：由勾股定理得 ，又，，所以所以五个小矩形的周长之和为
18. 分析：由角平分线的性质可得到，再根据平行线的性质可推出，利用SAS即可判定，由全等三角形的性质得，再分或确定四边形的形状．
解：∵ 平分，∴ .
∵，∴ .
∴ .∴ .
∵，∴.∴.
∵，∴,
∴.∵,∴ △≌△,
∴ ∠KBD=∠CDB.
（1）当时，四边形是等腰梯形．理由如下：
∵，平分,∴与不垂直.
∴.∴ 与不平行.
∴ 四边形是等腰梯形.
（2）当时，四边形是矩形．理由如下：
∵，平分,∴与垂直，
∴ ∠DBK=∠BDC=90°,∴ CD BK.∴ 四边形是矩形.
点拨：此题考查了学生对等腰梯形的判定、矩形的判定的理解及运用．
19.解：∵ ∥，∴ .
又∵ ，∴ ∠ , ∴ ∥ ,
∴ 四边形是平行四边形 ,
∴
∴ 四边形的周长.
20.证明：∵ 四边形是平行四边形，
∴ ∥，，
∴
∴ △≌△，故.
21.证明:∵ 四边形是平行四边形,∴
∴ .
在和中，，
∴，∴ .
22.（1）证明：在△和△中，，，
∴ △≌△．
（2）解．证明如下：∵ ∥，∥，
∴ 四边形是平行四边形．
由（1）知，∠=∠，∴ ，
∴ 四边形是菱形．∴ .
23.（1）证明：，∴ ．
在和中，
∴ ，∴ .
又，∴ 四边形是平行四边形．
，∴ 四边形是菱形．
（2）解： 四边形是菱形 ，，
∴ ．
在中，，∴ ，
∴．
∴
24.（1）证明：∵ 四边形是正方形，
∴ ∠∠，．
∵△是等边三角形，∴ ∠∠，．
∵∠∠，∠∠，
∴ ∠∠．
∵ ，∠∠，
∴△≌△．
（2）解：∵ △≌△，∴ ，
∴ ∠∠．
∵ ∠∠，∠∠，∠∠，
∴ ∠∠．
∵ ，∴ ∠∠．
∵ ∠，∴ ∠，
∴ ∠．
第2题图图