苏教版数学六年级上册 第一单元 长方体和正方体-表面涂色的正方体课件(共24张PPT)
文档属性
| 名称 | 苏教版数学六年级上册 第一单元 长方体和正方体-表面涂色的正方体课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 07:12:36 | ||
图片预览



文档简介
(共24张PPT)
表面涂色的正方体
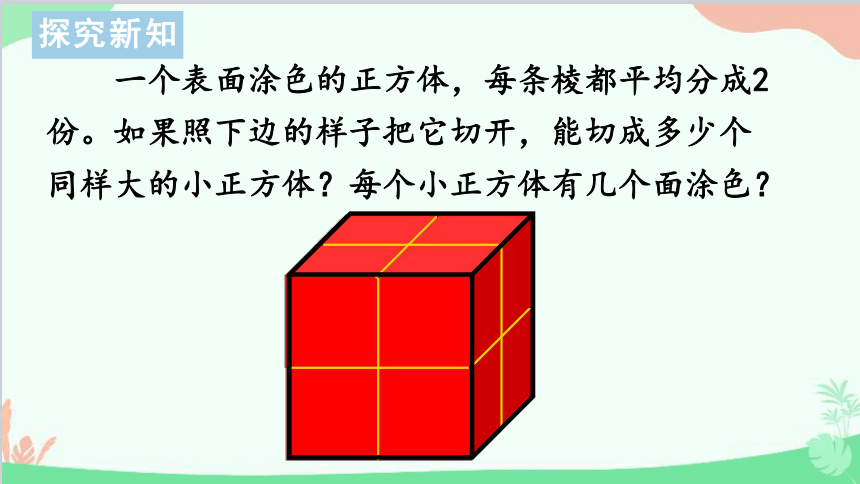
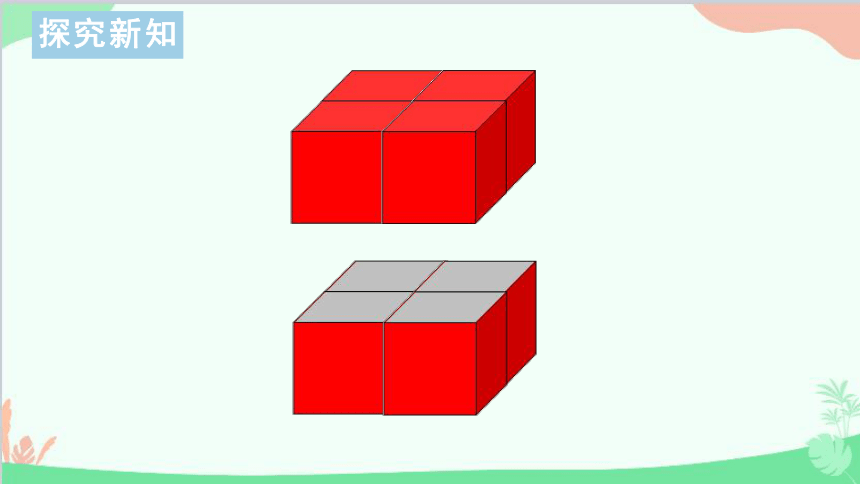
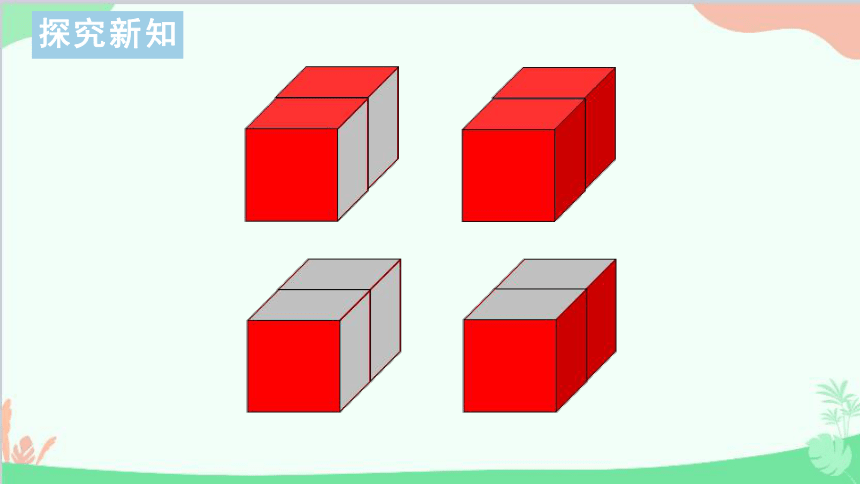
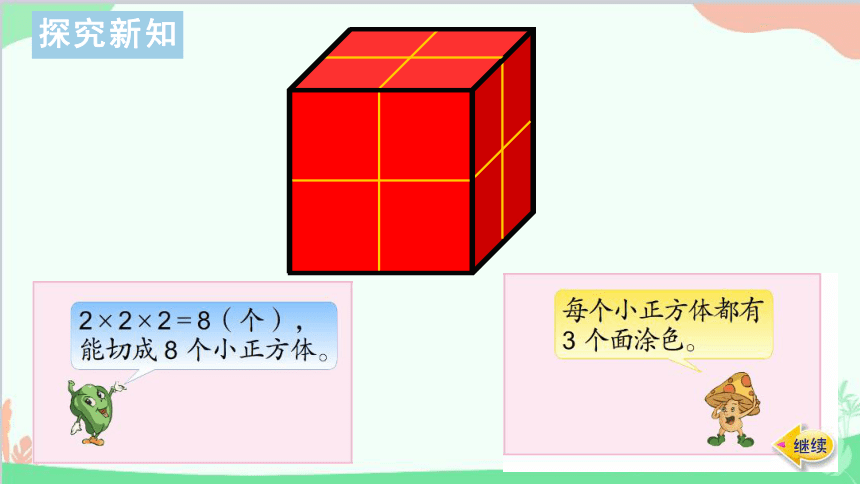
一个表面涂色的正方体,每条棱都平均分成2份。如果照下边的样子把它切开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
探究新知
探究新知
探究新知
探究新知
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方体中,3面涂色、2面涂色、1面涂色的各有多少个,分别在什么位置?
探究新知
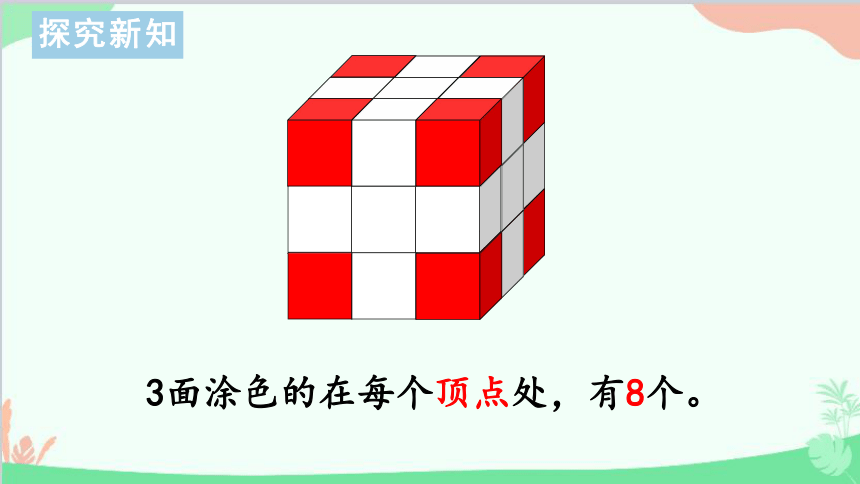
3面涂色的在每个顶点处,有8个。
探究新知
2面涂色的在每条棱的中间位置处,有12个。
探究新知
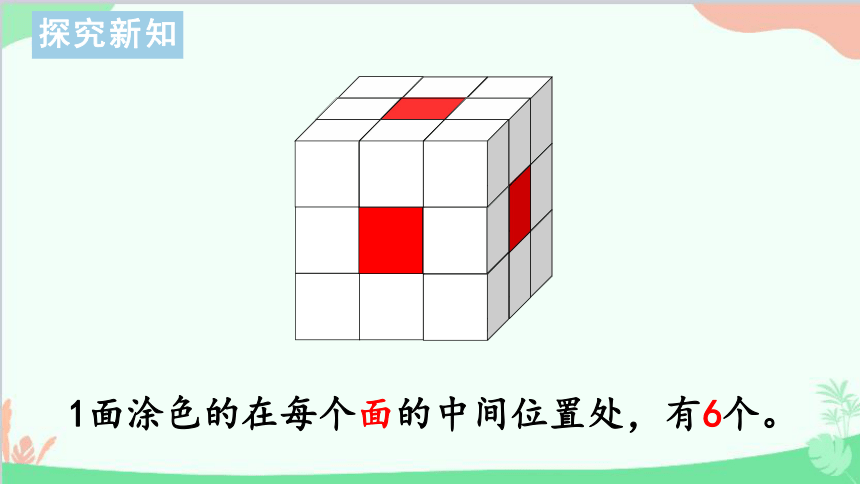
1面涂色的在每个面的中间位置处,有6个。
探究新知
如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?
探究新知
3面涂色的小正方体有8个。
探究新知
2面涂色的小正方体有24个。
2×12=24(个)
探究新知
探究新知
1面涂色的小正方体有24个。
22×6=24(个)
探究新知
3面涂色的小正方体有8个。
探究新知
2面涂色的小正方体有36个。
3×12=36(个)
探究新知
1面涂色的小正方体有54个。
32×6=54(个)
探究新知
探究新知
3面涂色的小正方体都在大正方体顶点的位置,都是8个。
探究新知
2面涂色的小正方体的个数都是12的倍数。
1×12=12
2×12=24
3×12=36
探究新知
1面涂色的小正方体的个数都是6的倍数。
12×6=6
22×6=24
32×6=54
探究新知
如果用n表示把大正方体的棱平均分的份数,用a、b分别表示
2面涂色和1面涂色的小正方体的个数,你能用式子分别表示n
和a、b的关系吗?
a=12(n-2)
b=6(n-2)2
探究新知
找各种小正方体时,要注意它们在大正方体上的位置。
各种小正方体的个数与正方体顶点、面和棱的个(条)数有关。
要把找、数、算等方法结合起来,并根据图形的特征进行思考。
探究新知
把棱长为几厘米的小正方体涂色后切成棱长为1厘米的小正方体,涂色面的规律:
(1)3面涂色的小正方体个数=正方体的顶点个数=8个;
(2)2面涂色的小正方体个数
=正方体棱的条数乘棱长减2的差
=12×(n-2);
(3)1面涂色的小正方体个数
=正方体的面数乘棱长减2的差的平方
=6×(n-2) 。
课堂小结
表面涂色的正方体
一个表面涂色的正方体,每条棱都平均分成2份。如果照下边的样子把它切开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
探究新知
探究新知
探究新知
探究新知
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方体中,3面涂色、2面涂色、1面涂色的各有多少个,分别在什么位置?
探究新知
3面涂色的在每个顶点处,有8个。
探究新知
2面涂色的在每条棱的中间位置处,有12个。
探究新知
1面涂色的在每个面的中间位置处,有6个。
探究新知
如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?
探究新知
3面涂色的小正方体有8个。
探究新知
2面涂色的小正方体有24个。
2×12=24(个)
探究新知
探究新知
1面涂色的小正方体有24个。
22×6=24(个)
探究新知
3面涂色的小正方体有8个。
探究新知
2面涂色的小正方体有36个。
3×12=36(个)
探究新知
1面涂色的小正方体有54个。
32×6=54(个)
探究新知
探究新知
3面涂色的小正方体都在大正方体顶点的位置,都是8个。
探究新知
2面涂色的小正方体的个数都是12的倍数。
1×12=12
2×12=24
3×12=36
探究新知
1面涂色的小正方体的个数都是6的倍数。
12×6=6
22×6=24
32×6=54
探究新知
如果用n表示把大正方体的棱平均分的份数,用a、b分别表示
2面涂色和1面涂色的小正方体的个数,你能用式子分别表示n
和a、b的关系吗?
a=12(n-2)
b=6(n-2)2
探究新知
找各种小正方体时,要注意它们在大正方体上的位置。
各种小正方体的个数与正方体顶点、面和棱的个(条)数有关。
要把找、数、算等方法结合起来,并根据图形的特征进行思考。
探究新知
把棱长为几厘米的小正方体涂色后切成棱长为1厘米的小正方体,涂色面的规律:
(1)3面涂色的小正方体个数=正方体的顶点个数=8个;
(2)2面涂色的小正方体个数
=正方体棱的条数乘棱长减2的差
=12×(n-2);
(3)1面涂色的小正方体个数
=正方体的面数乘棱长减2的差的平方
=6×(n-2) 。
课堂小结
