人教A版选修二 5.2.1 基本初等函数的导数 课件(共15张PPT)
文档属性
| 名称 | 人教A版选修二 5.2.1 基本初等函数的导数 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 599.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 15:15:44 | ||
图片预览





文档简介
(共15张PPT)
5.2.1 基本初等函数的导数
册 别:选择性必修二
学 科:高中数学
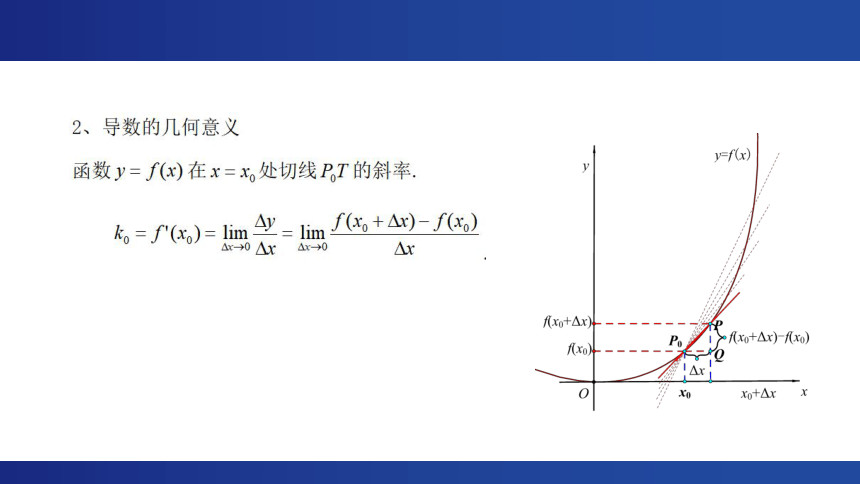
一、复习回顾
思考:如何利用定义求出 y=c ,y=x,y=x2, 的导数?
二、新知学习
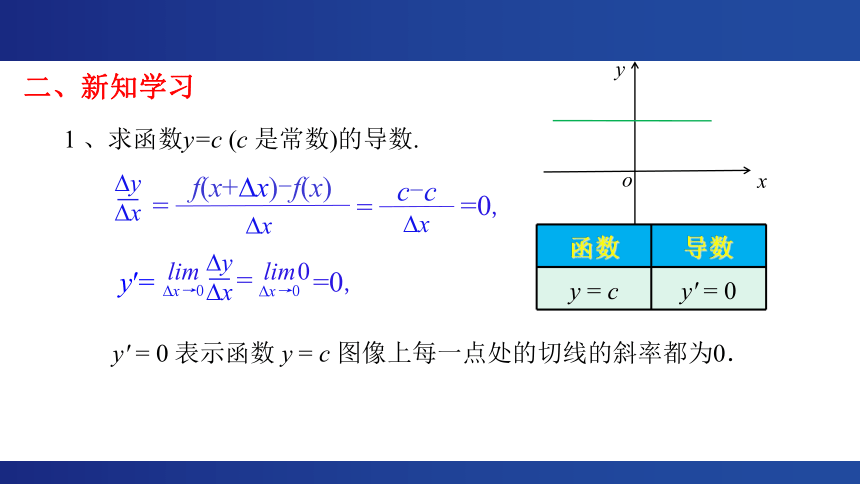
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
o
x
y
函数 导数
y = c y' = 0
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
o
x
y
结合函数的图象及其导数发现:
当x<0时,随着x的增加,函数减少得越来越快;
当x>0时,随着x的增加,函数减少得越来越慢.
6.求函数 的导数
函数 导数
o
x
y
结合函数的图象及其导数发现:
当时,随着x的增加,函数增加得越来越慢.
基本初等函数的导数公式
原函数 导函数
f(x)=c f ′(x)=0
f(x)=xn(n∈Q) f ′(x)=n·xn-1
f(x)=sinx f ′(x)=cosx
f(x)=cosx f ′(x)=-sinx
f(x)=ax f ′(x)=axlna
f(x)=ex f ′(x)=ex
f(x)=logax f ′(x)=
f(x)=lnx f ′(x)=
三、课堂练习
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
例1、求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
例2、求下列函数在给定点处的导数
例3、求余弦曲线 在点 处的切线方程.
注意:利用导数公式求导时,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
三、课堂小结
5.2.1 基本初等函数的导数
册 别:选择性必修二
学 科:高中数学
一、复习回顾
思考:如何利用定义求出 y=c ,y=x,y=x2, 的导数?
二、新知学习
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
o
x
y
函数 导数
y = c y' = 0
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
o
x
y
结合函数的图象及其导数发现:
当x<0时,随着x的增加,函数减少得越来越快;
当x>0时,随着x的增加,函数减少得越来越慢.
6.求函数 的导数
函数 导数
o
x
y
结合函数的图象及其导数发现:
当时,随着x的增加,函数增加得越来越慢.
基本初等函数的导数公式
原函数 导函数
f(x)=c f ′(x)=0
f(x)=xn(n∈Q) f ′(x)=n·xn-1
f(x)=sinx f ′(x)=cosx
f(x)=cosx f ′(x)=-sinx
f(x)=ax f ′(x)=axlna
f(x)=ex f ′(x)=ex
f(x)=logax f ′(x)=
f(x)=lnx f ′(x)=
三、课堂练习
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
例1、求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
例2、求下列函数在给定点处的导数
例3、求余弦曲线 在点 处的切线方程.
注意:利用导数公式求导时,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
三、课堂小结
