2.1.4 整式 课件(共26张PPT)
文档属性
| 名称 | 2.1.4 整式 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
整式
(第四课时)
复习引入
1
一条河的水流速度是 ,船在静水中的速度是 ,则船在这条河中顺水行驶速度是 ,在逆水行驶时是 ;
分析
顺水行驶时,船的速度船在静水中的速度水流速度
逆水行驶时,船的速度船在静水中的速度水流速度
列式表示
2
3
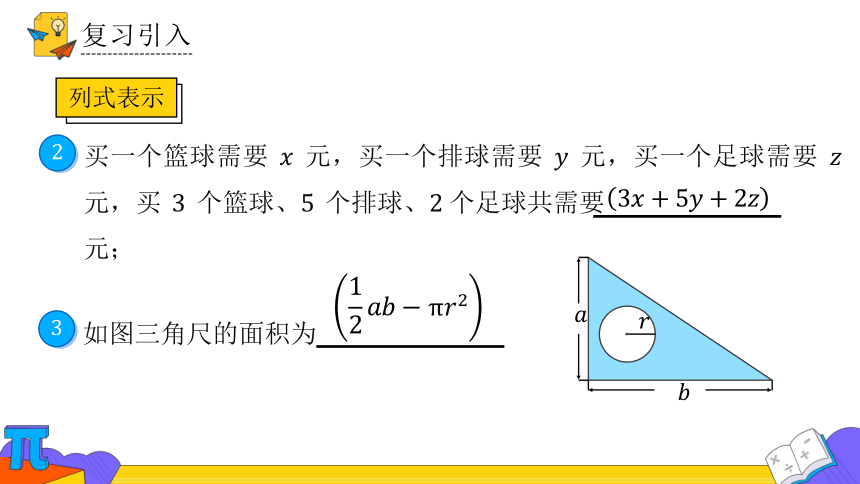
如图三角尺的面积为 .
复习引入
列式表示
买一个篮球需要 元,买一个排球需要 元,买一个足球需要 元,买 个篮球、 个排球、个足球共需要 元;
4
如图是一个建筑平面图(图中长度单位:),则该住宅的建筑面积是 .
复习引入
列式表示
讲授新知
观察
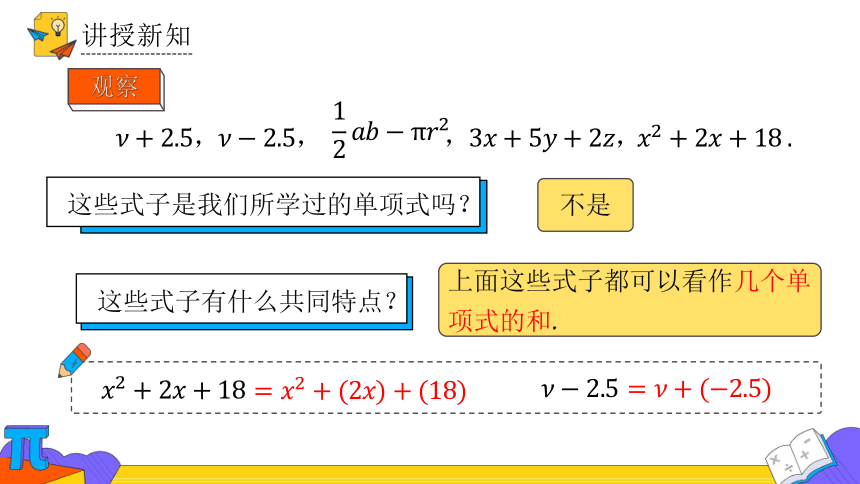
,
,
,
,
这些式子是我们所学过的单项式吗?
这些式子有什么共同特点?
不是
上面这些式子都可以看作几个单项式的和.
其中,不含字母的项,叫做常数项.
讲授新知
1
像这样,几个单项式的和叫做多项式.
在多项式中,每个单项式叫做多项式的项,
例如,多项式的项是,与,其中 是常数项;
多项式 的项是 与,其中是常数项.
多项式的各项应包括它前面的符号.
注意
讲授新知
2
多项式里,次数最高项的次数,叫做这个多项式的次数.
多项式次数是 .
例如,三项,与
是二次项,是一次项,常数项,次数最高项是二次项 .
次数最高项是一次项 ;
例如,多两项 与
是一次项,是常数项,
多项式 的次数是 .
讲授新知
3
单项式与多项式统称为整式.
举例
如:,
,
,
都是整式.
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , ;
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , 与 ;
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , 与 ;
整体是作为常数项.
注意
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 ,,
与;
小结
1
多项式的各项应包括它前面的符号.
如: 的项是与
2
多项式里,次数最高项的次数,叫做这个多项式的次数.
如:多项式 的次数是
如何快速准确找出多项式的项和次数:
3
一个多项式的最高次项可以不唯一.
如:
想一想
已知多项式 的次数是 , 的值为 .
因为多项式 的次数是 ,
分析
所以 的次数是 .
所以 .
例题讲解
例2
判断下列说法是否正确,并说明理由:
1
多项式 的一次项系数是; ( )
分析
例题讲解
例2
判断下列说法是否正确,并说明理由:
2
多项式 的次数是 ; ( )
分析
常数项
次数是
例题讲解
例2
判断下列说法是否正确,并说明理由:
3
是多项式; ( )
分析
例题讲解
例2
判断下列说法是否正确,并说明理由:
4
的次数是 ; ( )
分析
次数是
1
多项式与单项式概念的区别与联系;
表示数或字母的积的式子叫做单项式.
如:;
几个单项式的和叫做多项式.
如:;
小结
2
多项式与单项式次数的区别;
单项式中所有字母的指数的和叫做这个单项式的次数.
如:的次数是 ;
多项式里,次数最高项的次数,叫做这个多项式的次数.
如:次数是 ;
小结
例题讲解
例3
如图,用式子表示圆环的面积,当, 时,求圆环的面积.
解:外圆面积减去内圆面积就是圆环的面积,
所以圆环的面积是 .
当 ,时,圆环的面积(单位:)
这个圆环的面积是 .
课堂练习
填空:
, 分别表示长方形的长和宽,则长方形的周长
1
,面积 ,当
时, ,
, 分别表示梯形的上底和下底, 表示梯形的高,则梯形面积
,当时,, .
课堂练习
填空:
2
几个单项式的和叫做多项式.
课
堂
小
结
多项式中的每个单项式叫做
多项式的项,
1
多项式;
例如, 三项, 与 ,其中 是常数项.
其中,不含字母的项叫做常数项.
多项式里次数最高项的次数叫做多项式的次数.
课
堂
小
结
2
多项式的次数;
例如,多项式
3
整式.
单项式与多项式统称为整式.
再 见
整式
(第四课时)
复习引入
1
一条河的水流速度是 ,船在静水中的速度是 ,则船在这条河中顺水行驶速度是 ,在逆水行驶时是 ;
分析
顺水行驶时,船的速度船在静水中的速度水流速度
逆水行驶时,船的速度船在静水中的速度水流速度
列式表示
2
3
如图三角尺的面积为 .
复习引入
列式表示
买一个篮球需要 元,买一个排球需要 元,买一个足球需要 元,买 个篮球、 个排球、个足球共需要 元;
4
如图是一个建筑平面图(图中长度单位:),则该住宅的建筑面积是 .
复习引入
列式表示
讲授新知
观察
,
,
,
,
这些式子是我们所学过的单项式吗?
这些式子有什么共同特点?
不是
上面这些式子都可以看作几个单项式的和.
其中,不含字母的项,叫做常数项.
讲授新知
1
像这样,几个单项式的和叫做多项式.
在多项式中,每个单项式叫做多项式的项,
例如,多项式的项是,与,其中 是常数项;
多项式 的项是 与,其中是常数项.
多项式的各项应包括它前面的符号.
注意
讲授新知
2
多项式里,次数最高项的次数,叫做这个多项式的次数.
多项式次数是 .
例如,三项,与
是二次项,是一次项,常数项,次数最高项是二次项 .
次数最高项是一次项 ;
例如,多两项 与
是一次项,是常数项,
多项式 的次数是 .
讲授新知
3
单项式与多项式统称为整式.
举例
如:,
,
,
都是整式.
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , ;
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , 与 ;
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 , 与 ;
整体是作为常数项.
注意
例题讲解
例1
指出下列多项式的项和次数,是几次几项式?
解:项是 ,,
与;
小结
1
多项式的各项应包括它前面的符号.
如: 的项是与
2
多项式里,次数最高项的次数,叫做这个多项式的次数.
如:多项式 的次数是
如何快速准确找出多项式的项和次数:
3
一个多项式的最高次项可以不唯一.
如:
想一想
已知多项式 的次数是 , 的值为 .
因为多项式 的次数是 ,
分析
所以 的次数是 .
所以 .
例题讲解
例2
判断下列说法是否正确,并说明理由:
1
多项式 的一次项系数是; ( )
分析
例题讲解
例2
判断下列说法是否正确,并说明理由:
2
多项式 的次数是 ; ( )
分析
常数项
次数是
例题讲解
例2
判断下列说法是否正确,并说明理由:
3
是多项式; ( )
分析
例题讲解
例2
判断下列说法是否正确,并说明理由:
4
的次数是 ; ( )
分析
次数是
1
多项式与单项式概念的区别与联系;
表示数或字母的积的式子叫做单项式.
如:;
几个单项式的和叫做多项式.
如:;
小结
2
多项式与单项式次数的区别;
单项式中所有字母的指数的和叫做这个单项式的次数.
如:的次数是 ;
多项式里,次数最高项的次数,叫做这个多项式的次数.
如:次数是 ;
小结
例题讲解
例3
如图,用式子表示圆环的面积,当, 时,求圆环的面积.
解:外圆面积减去内圆面积就是圆环的面积,
所以圆环的面积是 .
当 ,时,圆环的面积(单位:)
这个圆环的面积是 .
课堂练习
填空:
, 分别表示长方形的长和宽,则长方形的周长
1
,面积 ,当
时, ,
, 分别表示梯形的上底和下底, 表示梯形的高,则梯形面积
,当时,, .
课堂练习
填空:
2
几个单项式的和叫做多项式.
课
堂
小
结
多项式中的每个单项式叫做
多项式的项,
1
多项式;
例如, 三项, 与 ,其中 是常数项.
其中,不含字母的项叫做常数项.
多项式里次数最高项的次数叫做多项式的次数.
课
堂
小
结
2
多项式的次数;
例如,多项式
3
整式.
单项式与多项式统称为整式.
再 见
