1.4.1.2 有理数的乘法 课件(共22张PPT)
文档属性
| 名称 | 1.4.1.2 有理数的乘法 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-28 21:29:19 | ||
图片预览








文档简介
(共22张PPT)
有理数的乘法
(第二课时)
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与相乘,都得.
复习
有理数乘法法则
1
2
3
(两数相乘,异号得负,并把绝对值相乘)
(两数相乘,同号得正,并把绝对值相乘)
(任何数与相乘,都得)
计算
观察
乘积是的两个数互为倒数.
我们说和 互为倒数
和 互为倒数,
和互为倒数,
和 互为倒数.
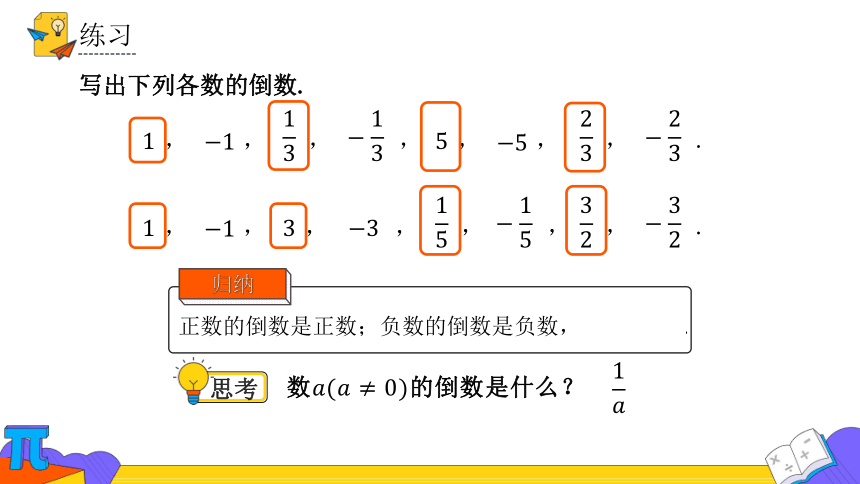
练习
写出下列各数的倒数.
正数的倒数是正数;负数的倒数是负数,没有倒数.
归纳
数的倒数是什么?
,
,
,
,
,
,
,
.
,
,
,
,
.
思考
,
,
,
归纳概括
1
2
3
4
观察下列各式,它们的积是正的还是负的?
议一议
思考
几个不是的数相乘,积的符号与负因数的个数之间有什么关系?
归纳概括
1
2
3
4
观察下列各式,它们的积是正的还是负的?
议一议
思考
几个不是的数相乘,积的符号与负因数的个数之间有什么关系?
几个不是的数相乘,积的符号由负因数的个数决定.
当负因数的个数是偶数时,积为正;
当负因数的个数是奇数时,积为负.
简记为“奇负偶正”.
11
多个有理数相乘的积的符号规律
例题示范
计算:
例1
1
负因数个数为奇数,积为负,再把绝对值相乘.
解:
1
例题示范
计算:
例1
2
负因数个数为偶数,积为正,再把绝对值相乘.
解:
2
你能看出下式的结果吗?如果能,请说明理由.
思考
几个数相乘,如果其中有因数为,积等于.
11
多个有理数乘法运算步骤
先观察是否有因数为;
1
确定积的符号(奇负偶正);
2
确定积的绝对值.
3
计算:
1
负因数个数为奇数,积为负,再把绝对值相乘.
小数化成分数.
解:
1
练习
计算:
2
负因数个数为奇数,积为负,再把绝对值相乘.
带分数化成假分数.
解:
2
练习
计算:
3
负因数个数为偶数,积为正,再把绝对值相乘.
小数化成假分数.
解:
3
练习
计算:
4
几个数相乘,如果其中有因数为0,积等于0.
先观察是否有因数.
解:
4
练习
课堂小结
一、倒数
倒数定义:
正数的倒数是正数,比如和 ;
负数的倒数是负数,比如 和;
没有倒数;
1
2
3
数的倒数是 .
课堂小结
二、多个有理数相乘的积的符号规律
几个不是的数相乘,积的符号由负因数的个数决定,简记为“奇负偶正”.
例如:
课堂小结
三、运算步骤
先观察是否有因数,再确定积的符号和绝对值.
例如:
课后思考
桌上有张反面向上的扑克牌,每次翻动其中任意张(包括已翻过的牌),使它们从一面向上变为另一面向上,这样一直做下去,观察能否使所有的牌都正面向上?
翻牌游戏
小学学习的乘法交换律、结合律与分配律在有理数乘法运算中是否依然成立?
思考
再 见
有理数的乘法
(第二课时)
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与相乘,都得.
复习
有理数乘法法则
1
2
3
(两数相乘,异号得负,并把绝对值相乘)
(两数相乘,同号得正,并把绝对值相乘)
(任何数与相乘,都得)
计算
观察
乘积是的两个数互为倒数.
我们说和 互为倒数
和 互为倒数,
和互为倒数,
和 互为倒数.
练习
写出下列各数的倒数.
正数的倒数是正数;负数的倒数是负数,没有倒数.
归纳
数的倒数是什么?
,
,
,
,
,
,
,
.
,
,
,
,
.
思考
,
,
,
归纳概括
1
2
3
4
观察下列各式,它们的积是正的还是负的?
议一议
思考
几个不是的数相乘,积的符号与负因数的个数之间有什么关系?
归纳概括
1
2
3
4
观察下列各式,它们的积是正的还是负的?
议一议
思考
几个不是的数相乘,积的符号与负因数的个数之间有什么关系?
几个不是的数相乘,积的符号由负因数的个数决定.
当负因数的个数是偶数时,积为正;
当负因数的个数是奇数时,积为负.
简记为“奇负偶正”.
11
多个有理数相乘的积的符号规律
例题示范
计算:
例1
1
负因数个数为奇数,积为负,再把绝对值相乘.
解:
1
例题示范
计算:
例1
2
负因数个数为偶数,积为正,再把绝对值相乘.
解:
2
你能看出下式的结果吗?如果能,请说明理由.
思考
几个数相乘,如果其中有因数为,积等于.
11
多个有理数乘法运算步骤
先观察是否有因数为;
1
确定积的符号(奇负偶正);
2
确定积的绝对值.
3
计算:
1
负因数个数为奇数,积为负,再把绝对值相乘.
小数化成分数.
解:
1
练习
计算:
2
负因数个数为奇数,积为负,再把绝对值相乘.
带分数化成假分数.
解:
2
练习
计算:
3
负因数个数为偶数,积为正,再把绝对值相乘.
小数化成假分数.
解:
3
练习
计算:
4
几个数相乘,如果其中有因数为0,积等于0.
先观察是否有因数.
解:
4
练习
课堂小结
一、倒数
倒数定义:
正数的倒数是正数,比如和 ;
负数的倒数是负数,比如 和;
没有倒数;
1
2
3
数的倒数是 .
课堂小结
二、多个有理数相乘的积的符号规律
几个不是的数相乘,积的符号由负因数的个数决定,简记为“奇负偶正”.
例如:
课堂小结
三、运算步骤
先观察是否有因数,再确定积的符号和绝对值.
例如:
课后思考
桌上有张反面向上的扑克牌,每次翻动其中任意张(包括已翻过的牌),使它们从一面向上变为另一面向上,这样一直做下去,观察能否使所有的牌都正面向上?
翻牌游戏
小学学习的乘法交换律、结合律与分配律在有理数乘法运算中是否依然成立?
思考
再 见
