12.3角的平分线的性质公开课
文档属性
| 名称 | 12.3角的平分线的性质公开课 |

|
|
| 格式 | zip | ||
| 文件大小 | 31.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-20 10:10:36 | ||
图片预览

文档简介
§12.3 角平分线的性质
学习目标
1、复分线的性质定理、判定定理
2、能够运用角平分线的性质定理、判定定理解决几何问题
学习重点和难点
重点:角平分线的性质定理、判定定理
难点:利用角平分线的性质定理、判定定理解决几何问题
学习过程
一、基础要点回顾
1、尺规作图
已知:∠AOB,
求作:∠AOB的平分线OC
2、用符号语言来表述角的平分线的性质定理符号语言
如上图,∵OC是∠AOB的平分线,点P是 OC上的一点,PEOB、PDOA
∴ ________________ 。
3、用数学语言来表述角的平分线的性质定理
定理:角平分线上的点到_________________距离相等;
二、思考:那么在角的内部,到角的两边距离相等的点是否在角的平分线上呢?
由此得角平分线的判定
用符号语言来表述角平分线的判定定理
1、如上图,∵点P是 OC上的一点,PEOB、PDOA ,PD=PE
∴________________是________________的平分线,
2、用数学语言来表述角的平分线的判定定理:
定理:角的内部到角的两边距离相等的点在_________的平分线上。
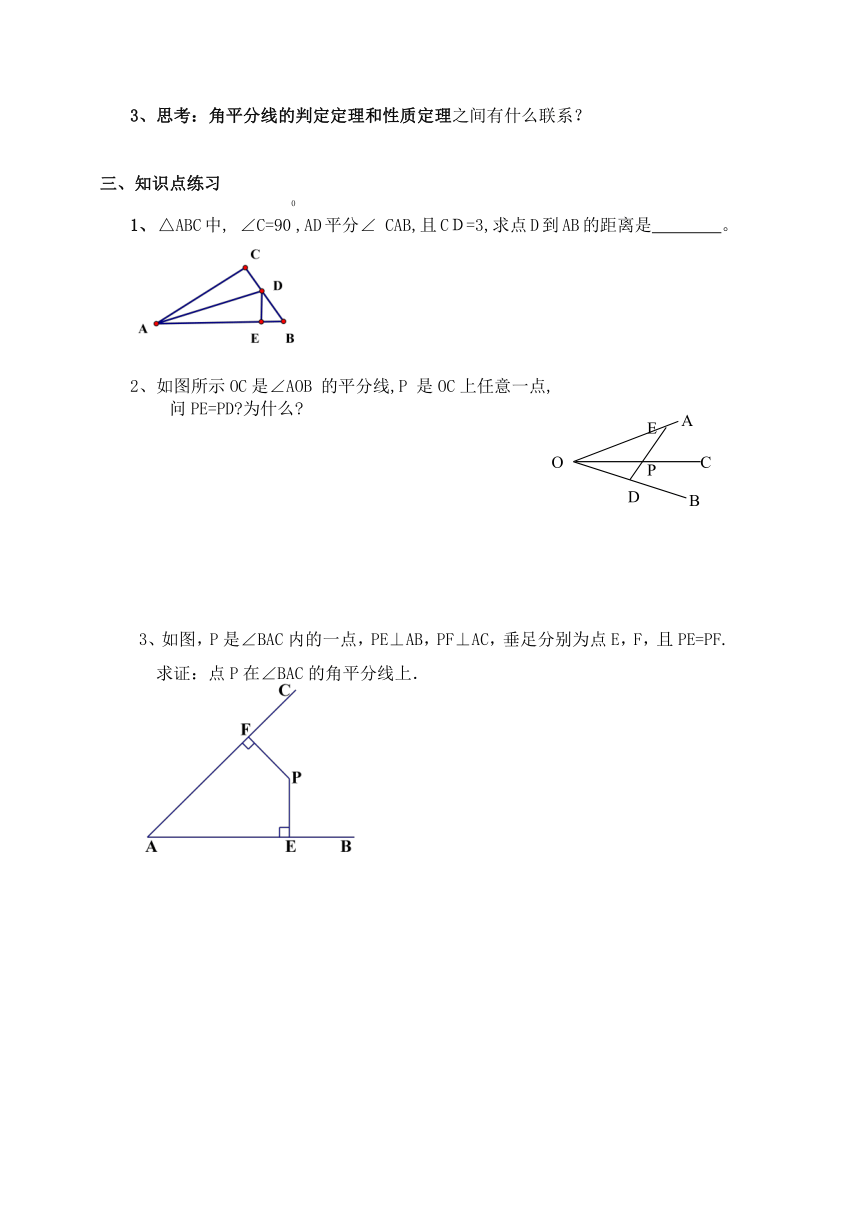
3、思考:角平分线的判定定理和性质定理之间有什么联系?
三、知识点练习
△ABC中, ∠C=900,AD平分∠ CAB,且CD=3,求点D到AB的距离是 。
2、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,
问PE=PD 为什么
3、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,且PE=PF.
求证:点P在∠BAC的角平分线上.
课堂检测
△ABC中, ∠C=900,AD平分∠ CAB,且BC=8,BD=5,求点D到AB的距离是 。
2、在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,
求BE,AE的长和△AED的周长。
3.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
五、谈谈课堂收获
六、课后兴趣题
1、如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
2、如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,
且CD:DB=1:2,则点D到AB的距离为_________。
3、如图,D、E、F分别是△ABC的三边上的点,CE=BF,DH⊥AB于H,DG⊥AC于G,△DCE和△DBF的面积相等. 求证:AD平分∠BAC.
4、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
O
A
B
E
D
C
P
E
D
C
B
A
_
H
_
G
_
M
_
E
_
F
_
D
_
C
_
B
_
A
学习目标
1、复分线的性质定理、判定定理
2、能够运用角平分线的性质定理、判定定理解决几何问题
学习重点和难点
重点:角平分线的性质定理、判定定理
难点:利用角平分线的性质定理、判定定理解决几何问题
学习过程
一、基础要点回顾
1、尺规作图
已知:∠AOB,
求作:∠AOB的平分线OC
2、用符号语言来表述角的平分线的性质定理符号语言
如上图,∵OC是∠AOB的平分线,点P是 OC上的一点,PEOB、PDOA
∴ ________________ 。
3、用数学语言来表述角的平分线的性质定理
定理:角平分线上的点到_________________距离相等;
二、思考:那么在角的内部,到角的两边距离相等的点是否在角的平分线上呢?
由此得角平分线的判定
用符号语言来表述角平分线的判定定理
1、如上图,∵点P是 OC上的一点,PEOB、PDOA ,PD=PE
∴________________是________________的平分线,
2、用数学语言来表述角的平分线的判定定理:
定理:角的内部到角的两边距离相等的点在_________的平分线上。
3、思考:角平分线的判定定理和性质定理之间有什么联系?
三、知识点练习
△ABC中, ∠C=900,AD平分∠ CAB,且CD=3,求点D到AB的距离是 。
2、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,
问PE=PD 为什么
3、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,且PE=PF.
求证:点P在∠BAC的角平分线上.
课堂检测
△ABC中, ∠C=900,AD平分∠ CAB,且BC=8,BD=5,求点D到AB的距离是 。
2、在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,
求BE,AE的长和△AED的周长。
3.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
五、谈谈课堂收获
六、课后兴趣题
1、如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
2、如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,
且CD:DB=1:2,则点D到AB的距离为_________。
3、如图,D、E、F分别是△ABC的三边上的点,CE=BF,DH⊥AB于H,DG⊥AC于G,△DCE和△DBF的面积相等. 求证:AD平分∠BAC.
4、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
O
A
B
E
D
C
P
E
D
C
B
A
_
H
_
G
_
M
_
E
_
F
_
D
_
C
_
B
_
A
