12.2.1三角形全等的判定SSS
文档属性
| 名称 | 12.2.1三角形全等的判定SSS |

|
|
| 格式 | zip | ||
| 文件大小 | 19.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-22 00:00:00 | ||
图片预览

文档简介
学 科 数学 年 级 八 主备人 总编号 8
课 题 12.2.1全等三角形的判定(sss)
课 时 第 1 课时(总 5课时) 课 型 新授 时间 2013年 9月 22日
教学目标 知识目标 掌握“边边边”条件的内容,并能初步应用“边边边”条件判定两个三角形全等 .
能力目标 使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力.
情感目标 通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
教学重点 利用边边边证明两个三角形全等
教学难点 探究三角形全等的条件
教法学法 启发式教学、小组自主合作学习
教学环节 教 学 过 程 设 计 修订与完善
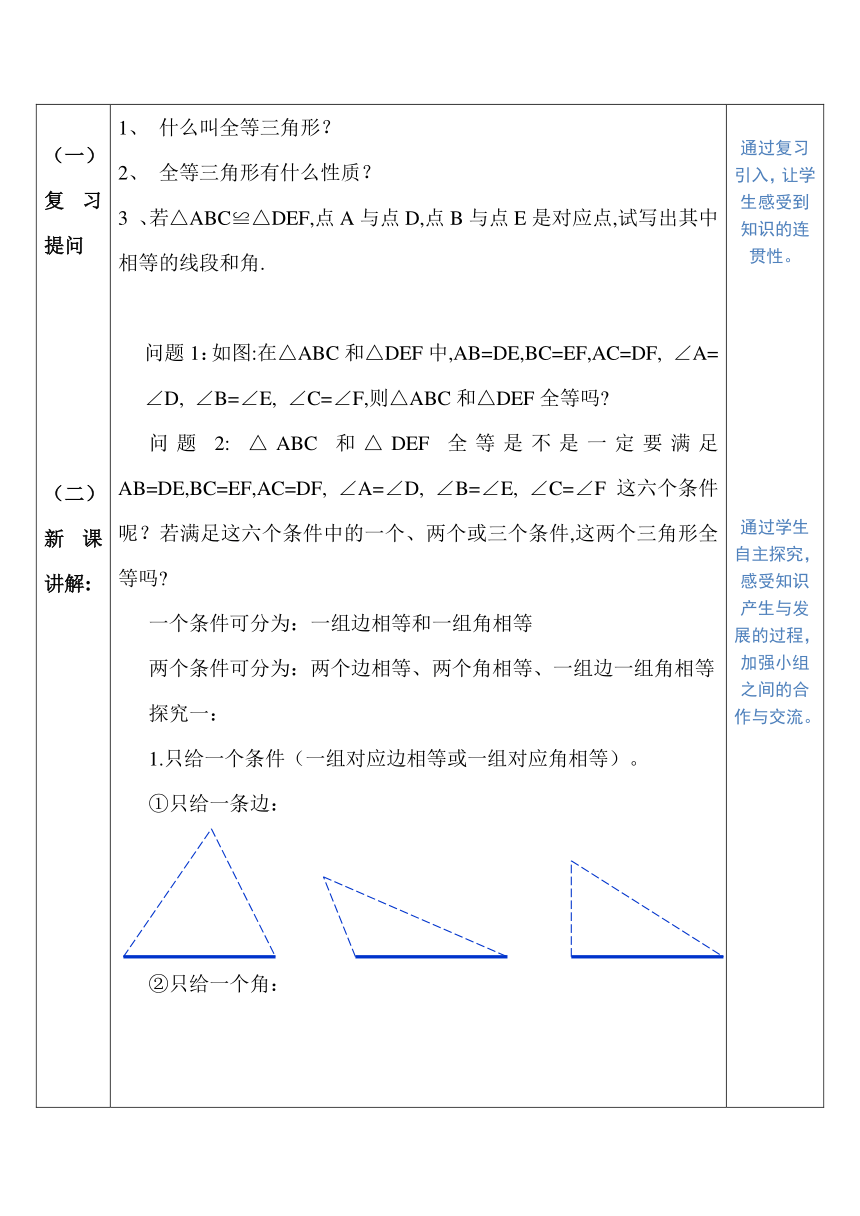
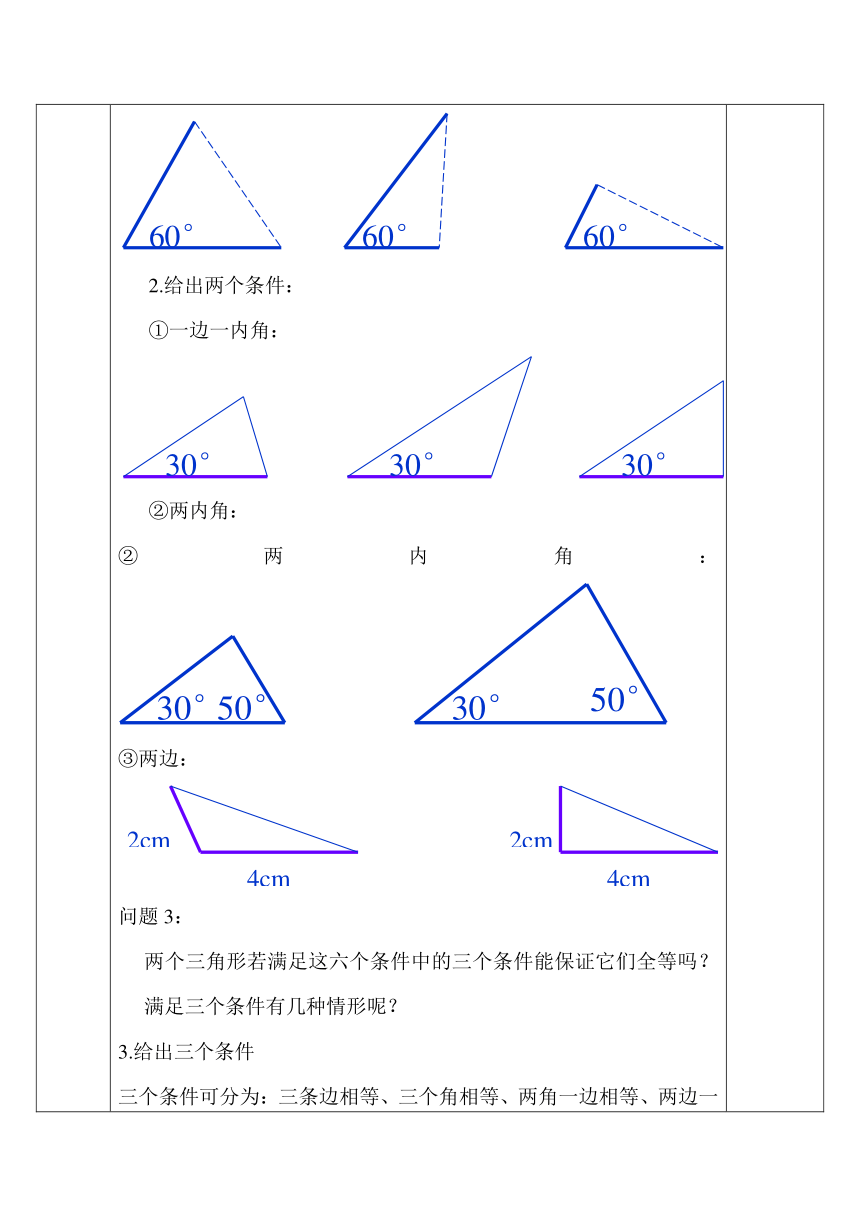
(一)复习提问(二)新课讲解:(三)题例训练: 1、 什么叫全等三角形?2、 全等三角形有什么性质?3 、若△ABC≌△DEF,点A与点D,点B与点E是对应点,试写出其中相等的线段和角.问题1:如图:在△ABC和△DEF中,AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F,则△ABC和△DEF全等吗 问题2: △ABC和△DEF全等是不是一定要满足AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F这六个条件呢?若满足这六个条件中的一个、两个或三个条件,这两个三角形全等吗 一个条件可分为:一组边相等和一组角相等两个条件可分为:两个边相等、两个角相等、一组边一组角相等探究一:1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:2.给出两个条件:①一边一内角:②两内角:②两内角:③两边:问题3:两个三角形若满足这六个条件中的三个条件能保证它们全等吗?满足三个条件有几种情形呢?3.给出三个条件三个条件可分为:三条边相等、三个角相等、两角一边相等、两边一角相等例:画△ABC,使AB=2,AC=3,BC=4画法:1画线段BC=4 2分别以A、B为圆心,以2和3为半径作弧,交于点C。则△ABC即为所求的三角形 把你画的三角形与其同桌所画的三角形剪下来,进行比较,它们能否互相重合?归纳:有三边对应相等的两个三角形全等.可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中AB=DEBC=EFCA=FD∴ △ABC ≌△ DEF(SSS)1、在下列推理中填写需要补充的条件,使结论成立: 如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)2、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 解: △ABC≌△DCB理由如下:在△ABC和△DCB中 AB = DC AC = DB ——=——∴△ABC ≌ ( )证明的书写步骤:①准备条件:证全等时把要用的条件要先证好;②三角形全等书写步骤:1写出在哪两个三角形中2摆出三个条件用大括号括起来3写出全等结论 通过复习引入,让学生感受到知识的连贯性。通过学生自主探究,感受知识产生与发展的过程,加强小组之间的合作与交流。尺规作图工具仅限圆规和直尺。
板书设计 12.2.1三角形全等的判定sss三角形全等的条件:三边分别相等的两个三角形全等(sss)例一:例二:例三:
教学反思 本节课从回顾全等三角形的性质入手,很自然的设问:满足六个条件中的一部分是否就能保证两个三角形全等?从此激起学生对全等三角形的判定条件的探究。通过动手操作,由满足一个条件、两个条件到满足三个条件的情况得出边边边的条件。
60°
60°
60°
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
AO=DO(已知)
______=________(已知)
BO=CO(已知)
课 题 12.2.1全等三角形的判定(sss)
课 时 第 1 课时(总 5课时) 课 型 新授 时间 2013年 9月 22日
教学目标 知识目标 掌握“边边边”条件的内容,并能初步应用“边边边”条件判定两个三角形全等 .
能力目标 使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力.
情感目标 通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
教学重点 利用边边边证明两个三角形全等
教学难点 探究三角形全等的条件
教法学法 启发式教学、小组自主合作学习
教学环节 教 学 过 程 设 计 修订与完善
(一)复习提问(二)新课讲解:(三)题例训练: 1、 什么叫全等三角形?2、 全等三角形有什么性质?3 、若△ABC≌△DEF,点A与点D,点B与点E是对应点,试写出其中相等的线段和角.问题1:如图:在△ABC和△DEF中,AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F,则△ABC和△DEF全等吗 问题2: △ABC和△DEF全等是不是一定要满足AB=DE,BC=EF,AC=DF, ∠A=∠D, ∠B=∠E, ∠C=∠F这六个条件呢?若满足这六个条件中的一个、两个或三个条件,这两个三角形全等吗 一个条件可分为:一组边相等和一组角相等两个条件可分为:两个边相等、两个角相等、一组边一组角相等探究一:1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:2.给出两个条件:①一边一内角:②两内角:②两内角:③两边:问题3:两个三角形若满足这六个条件中的三个条件能保证它们全等吗?满足三个条件有几种情形呢?3.给出三个条件三个条件可分为:三条边相等、三个角相等、两角一边相等、两边一角相等例:画△ABC,使AB=2,AC=3,BC=4画法:1画线段BC=4 2分别以A、B为圆心,以2和3为半径作弧,交于点C。则△ABC即为所求的三角形 把你画的三角形与其同桌所画的三角形剪下来,进行比较,它们能否互相重合?归纳:有三边对应相等的两个三角形全等.可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中AB=DEBC=EFCA=FD∴ △ABC ≌△ DEF(SSS)1、在下列推理中填写需要补充的条件,使结论成立: 如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)2、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 解: △ABC≌△DCB理由如下:在△ABC和△DCB中 AB = DC AC = DB ——=——∴△ABC ≌ ( )证明的书写步骤:①准备条件:证全等时把要用的条件要先证好;②三角形全等书写步骤:1写出在哪两个三角形中2摆出三个条件用大括号括起来3写出全等结论 通过复习引入,让学生感受到知识的连贯性。通过学生自主探究,感受知识产生与发展的过程,加强小组之间的合作与交流。尺规作图工具仅限圆规和直尺。
板书设计 12.2.1三角形全等的判定sss三角形全等的条件:三边分别相等的两个三角形全等(sss)例一:例二:例三:
教学反思 本节课从回顾全等三角形的性质入手,很自然的设问:满足六个条件中的一部分是否就能保证两个三角形全等?从此激起学生对全等三角形的判定条件的探究。通过动手操作,由满足一个条件、两个条件到满足三个条件的情况得出边边边的条件。
60°
60°
60°
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
AO=DO(已知)
______=________(已知)
BO=CO(已知)
