12.2.3 三角形全等判定
文档属性
| 名称 | 12.2.3 三角形全等判定 |
|
|
| 格式 | zip | ||
| 文件大小 | 29.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-22 00:00:00 | ||
图片预览


文档简介
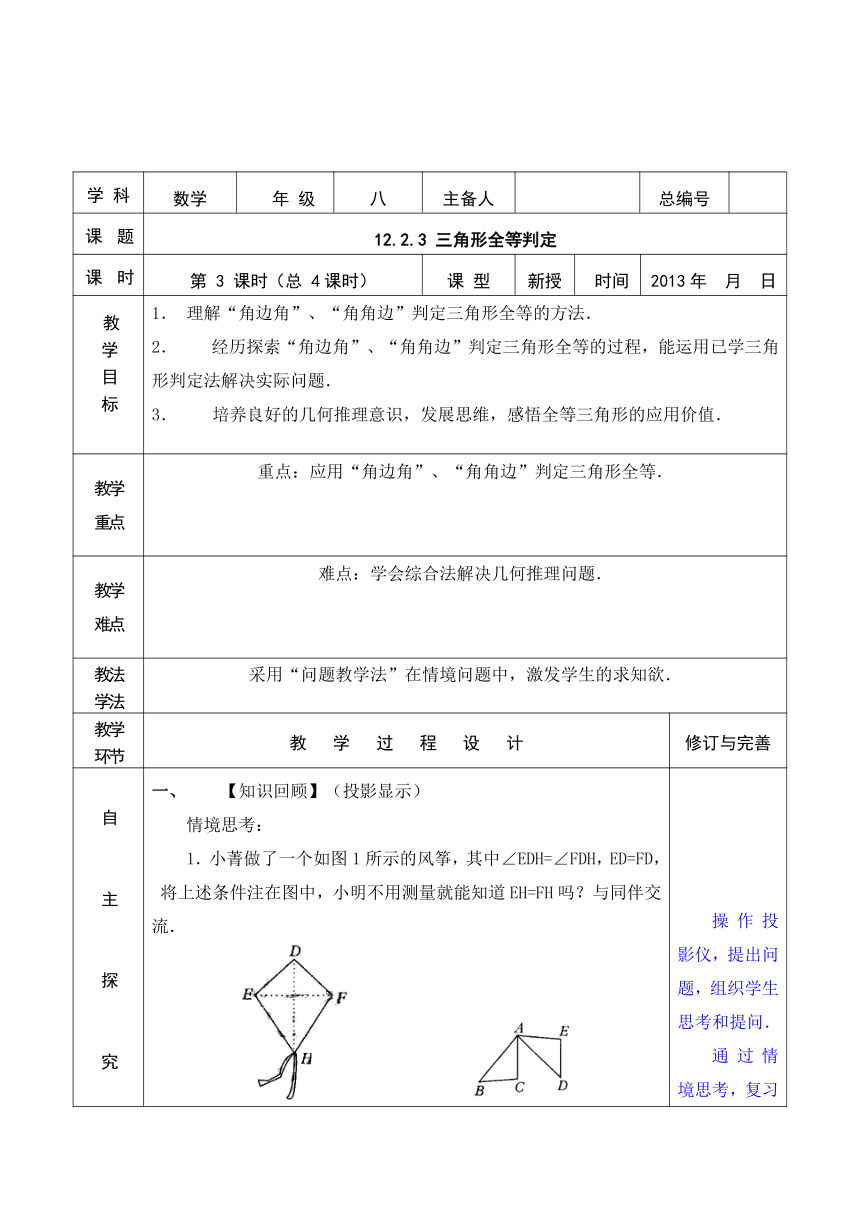
学 科 数学 年 级 八 主备人 总编号
课 题 12.2.3 三角形全等判定
课 时 第 3 课时(总 4课时) 课 型 新授 时间 2013年 月 日
教学目标 1. 理解“角边角”、“角角边”判定三角形全等的方法.2. 经历探索“角边角”、“角角边”判定三角形全等的过程,能运用已学三角形判定法解决实际问题.3. 培养良好的几何推理意识,发展思维,感悟全等三角形的应用价值.
教学重点 重点:应用“角边角”、“角角边”判定三角形全等.
教学难点 难点:学会综合法解决几何推理问题.
教法学法 采用“问题教学法”在情境问题中,激发学生的求知欲.
教学环节 教 学 过 程 设 计 修订与完善
自主探究 一、 【知识回顾】(投影显示) 情境思考: 1.小菁做了一个如图1所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件注在图中,小明不用测量就能知道EH=FH吗?与同伴交流. (1) (2) [答案:能,因为根据“SAS”,可以得到△EDH≌△FDH,从而EH=FH]2.如图2,AB=AD,AC=AE,能添上一个条件证明出△ABC≌△ADE吗?[答案:BC=DE(SSS)或∠BAC=∠DAE(SAS)]. 3.如果两边及其中一边的对角对应相等,两个三角形一定会全等吗?试举例说明. 【教师活动】操作投影仪,提出问题,组织学生思考和提问. 【学生活动】通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 【教学形式】用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲. 操作投影仪,提出问题,组织学生思考和提问. 通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲.
尝试应用 二【动手动脑】(投影显示) 问题探究:先任意画一个△ABC,再画出一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即使两角和它们的夹边对应相等),把画出的△A′B′C′剪下,放到△ABC上,它们全等吗?【学生活动】动手操作,感知问题的规律,画图如下: 画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B:画A′B′=AB;在A′B′的同旁画∠DA′B′=∠A,∠EBA′=∠B,A′D,B′E交于点C′。 探究规律:两角和它们的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”). 【知识铺垫】课本图11.2─8中,∠A′=∠A,∠B′=∠B,那么∠C=∠A′C′B′吗?为什么? 【学生回答】根据三角形内角和定理,∠C′=180°-∠A′-∠B′,∠C=180°-∠A-∠B,由于∠A=∠A′,∠B=∠B′,∴∠C=∠C′.【教师提问】在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF(课本图11.2─9),△ABC与△DEF全等吗? 【学生活动】运用三角形内角和定理,以及“ASA”很快证出△ABC≌△EFD,并且归纳如下: 归纳规律:两个角和其中一个角的对边对应相等的两个三角形全等(简与成AAS). 运用三角形内角和定理,以及“ASA”很快证出△ABC≌△EFD,并且归纳如下: 归纳规律:两个角和其中一个角的对边对应相等的两个三角形全等(简与成AAS).
补偿提高 三、【例3】如课本图11.2─10,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE.【教师活动】引导学生,分析例3.关键是寻找到和已知条件有关的△ACD和△ABE,再证它们全等,从而得出AD=AE.证明:在△ACD与△ABE中, ∴△ACD≌△ABE(ASA) ∴AD=AE 【学生活动】参与教师分析,领会推理方法. 【媒体使用】投影显示例3. 【教学形式】师生互动. 【教师提问】三角对应相等的两个三角形全等吗?【学生活动】与同伴交流,得到有三角对应相等的两个三角形不一定会全等,拿出三角板进行说明,如图3,下面这块三角形的内外边形成的△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,但是它们不全等.(形状相同,大小不等). 与同伴交流,得到有三角对应相等的两个三角形不一定会全等,拿出三角板进行说明,如图3,下面这块三角形的内外边形成的△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,但是它们不全等.
小结 1.证明两个三角形全等有几种方法?如何选择和应用这些方法? 2.全等三角形性质可以用来证明哪些问题?举例说明.
板书设计 把黑板分成三部分,左边部分板书“角边角”、“角角边”判定法,中间部分板书例题、画图,右边部分板书练习.
教学反思 通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲.
课 题 12.2.3 三角形全等判定
课 时 第 3 课时(总 4课时) 课 型 新授 时间 2013年 月 日
教学目标 1. 理解“角边角”、“角角边”判定三角形全等的方法.2. 经历探索“角边角”、“角角边”判定三角形全等的过程,能运用已学三角形判定法解决实际问题.3. 培养良好的几何推理意识,发展思维,感悟全等三角形的应用价值.
教学重点 重点:应用“角边角”、“角角边”判定三角形全等.
教学难点 难点:学会综合法解决几何推理问题.
教法学法 采用“问题教学法”在情境问题中,激发学生的求知欲.
教学环节 教 学 过 程 设 计 修订与完善
自主探究 一、 【知识回顾】(投影显示) 情境思考: 1.小菁做了一个如图1所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件注在图中,小明不用测量就能知道EH=FH吗?与同伴交流. (1) (2) [答案:能,因为根据“SAS”,可以得到△EDH≌△FDH,从而EH=FH]2.如图2,AB=AD,AC=AE,能添上一个条件证明出△ABC≌△ADE吗?[答案:BC=DE(SSS)或∠BAC=∠DAE(SAS)]. 3.如果两边及其中一边的对角对应相等,两个三角形一定会全等吗?试举例说明. 【教师活动】操作投影仪,提出问题,组织学生思考和提问. 【学生活动】通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 【教学形式】用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲. 操作投影仪,提出问题,组织学生思考和提问. 通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲.
尝试应用 二【动手动脑】(投影显示) 问题探究:先任意画一个△ABC,再画出一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即使两角和它们的夹边对应相等),把画出的△A′B′C′剪下,放到△ABC上,它们全等吗?【学生活动】动手操作,感知问题的规律,画图如下: 画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B:画A′B′=AB;在A′B′的同旁画∠DA′B′=∠A,∠EBA′=∠B,A′D,B′E交于点C′。 探究规律:两角和它们的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”). 【知识铺垫】课本图11.2─8中,∠A′=∠A,∠B′=∠B,那么∠C=∠A′C′B′吗?为什么? 【学生回答】根据三角形内角和定理,∠C′=180°-∠A′-∠B′,∠C=180°-∠A-∠B,由于∠A=∠A′,∠B=∠B′,∴∠C=∠C′.【教师提问】在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF(课本图11.2─9),△ABC与△DEF全等吗? 【学生活动】运用三角形内角和定理,以及“ASA”很快证出△ABC≌△EFD,并且归纳如下: 归纳规律:两个角和其中一个角的对边对应相等的两个三角形全等(简与成AAS). 运用三角形内角和定理,以及“ASA”很快证出△ABC≌△EFD,并且归纳如下: 归纳规律:两个角和其中一个角的对边对应相等的两个三角形全等(简与成AAS).
补偿提高 三、【例3】如课本图11.2─10,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE.【教师活动】引导学生,分析例3.关键是寻找到和已知条件有关的△ACD和△ABE,再证它们全等,从而得出AD=AE.证明:在△ACD与△ABE中, ∴△ACD≌△ABE(ASA) ∴AD=AE 【学生活动】参与教师分析,领会推理方法. 【媒体使用】投影显示例3. 【教学形式】师生互动. 【教师提问】三角对应相等的两个三角形全等吗?【学生活动】与同伴交流,得到有三角对应相等的两个三角形不一定会全等,拿出三角板进行说明,如图3,下面这块三角形的内外边形成的△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,但是它们不全等.(形状相同,大小不等). 与同伴交流,得到有三角对应相等的两个三角形不一定会全等,拿出三角板进行说明,如图3,下面这块三角形的内外边形成的△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,但是它们不全等.
小结 1.证明两个三角形全等有几种方法?如何选择和应用这些方法? 2.全等三角形性质可以用来证明哪些问题?举例说明.
板书设计 把黑板分成三部分,左边部分板书“角边角”、“角角边”判定法,中间部分板书例题、画图,右边部分板书练习.
教学反思 通过情境思考,复习前面学过的知识,学会正确选择三角形全等的判定方法,小组交流,踊跃发言. 用问题牵引,辨析、巩固已学知识,在师生互动交流过程中,激发求知欲.
