北师大版数学七年级上册 3.5 探索与表达规律 学案(2课时、含答案)
文档属性
| 名称 | 北师大版数学七年级上册 3.5 探索与表达规律 学案(2课时、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 19:17:20 | ||
图片预览




文档简介
5 探索与表达规律
第1课时 探索规律
学习目标
1.会用代数式表达规律,并能借助代数式的运算验证所探索的规律的一般性.(重难点)
2.经历探索数量关系、运用符号表达规律,体会探索规律的一般方法.(难点)
自主学习
学习任务 日历中的数字规律
观察教材第98页的日历图,回答下列问题.
1.(1)横行上相邻的两个数相差多少?
(2)如果用a表示横行上的第一个数,则与它相邻的右边的两个数分别表示为
与 .
2.(1)竖列上相邻的两个数相差多少?
(2)如果用a表示竖列上的最上面的数,则与它相邻的下面的两个数分别表示为
与 .
3.(1)斜列上从左上到右下相邻两数相差多少?从右上到左下相邻两数相差多少?
(2)如果用a表示左上的数,则与它相邻的右下的两个数分别表示为 与 ;如果用a表示右上的数,则与它相邻的左下的两个数分别表示为 与 .
4.如图1所示,如果用a表示日历图3×3方框(每个方框中都有数)中的中间数,请你填出方框中另外的8个数.
a
图1
合作探究
如图2所示,观察日历图,完成下列问题.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
图2
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?
(3)这个关系对任何一个月的日历都成立吗?为什么?
(4)你还能发现这样的方框中9个数之间的其他关系吗?
当堂达标
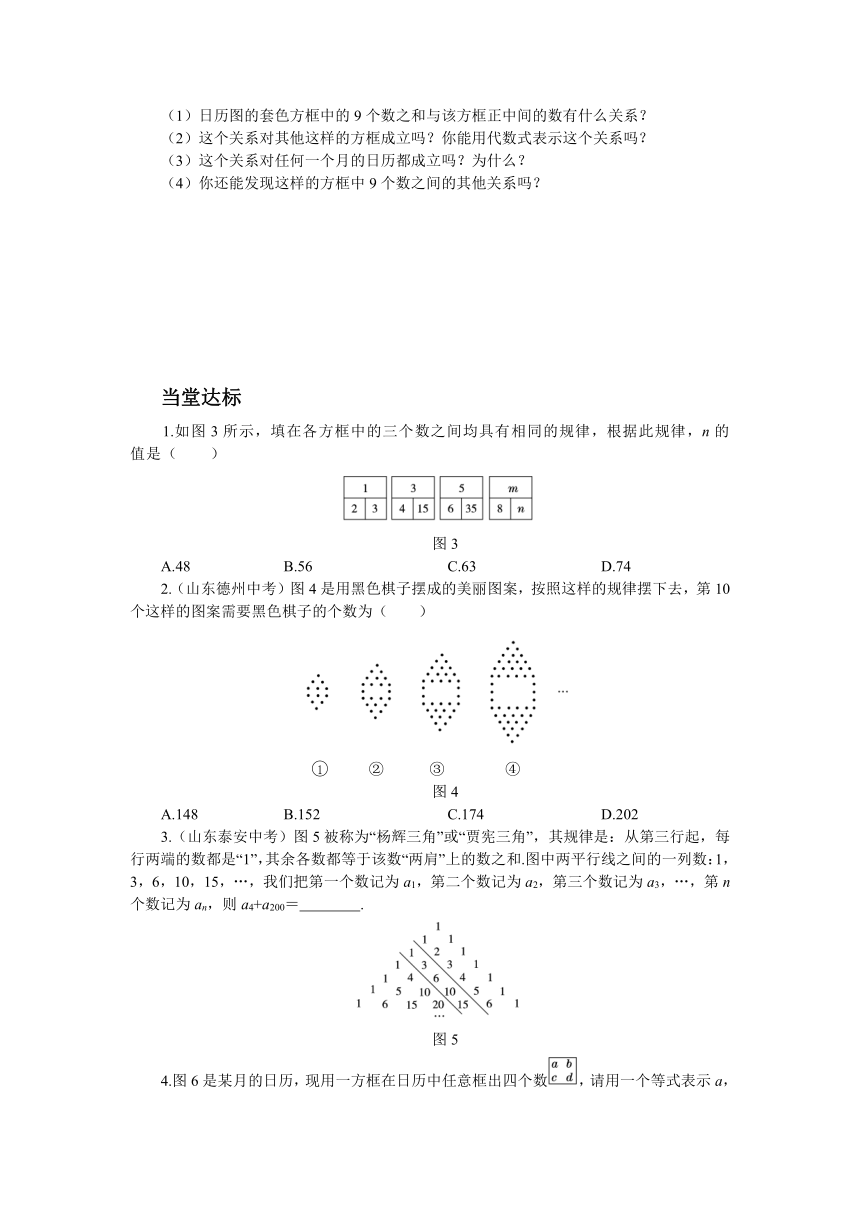
1.如图3所示,填在各方框中的三个数之间均具有相同的规律,根据此规律,n的值是( )
图3
A.48 B.56 C.63 D.74
2.(山东德州中考)图4是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )
② ③ ④
图4
A.148 B.152 C.174 D.202
3.(山东泰安中考)图5被称为“杨辉三角”或“贾宪三角”,其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.图中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,则a4+a200= .
图5
4.图6是某月的日历,现用一方框在日历中任意框出四个数,请用一个等式表示a,b,c,d之间的关系 (只要填一个即可).
日 一 二 三 四 五 六
1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30
图6
5.某数学活动小组的20名同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己的顺序数的倒数加1,第一位同学报,第二位同学报,第三位同学报,…,这样得到的20个数的积为 .
课后提升
1.某种数字游戏规律如下表所示:
A行 2 3 4 5 6 … 2 009
B行 1 2 3 4 5 … 2 008
C行 1 4 7 10 13 … x
按此规律,则表格中最右一栏中的x的值等于 .
2.从1开始的自然数按如图7所示的规则排列,并用一个平行四边形框出9个数,能否使这九个数的和等于①1 993;②1 143;③1 989?若能办到,请写出平行四边形框内的最大数和最小数;若不能办到,说明理由.
图7
反思感悟
我的收获:
我的易错点:
参考答案
自主学习
学习任务
1.(1)1 (2)a+1 a+2
2.(1)7 (2)a+7 a+14
3.(1)8 6 (2)a+8 a+16 a+6 a+12
4.解:
a-8 a-7 a-6
a-1 a a+1
a+6 a+7 a+8
合作探究
解:(1)9个数之和为90,90=10×9,这9个数之和是中间数的9倍.
(2)成立.设中间数为a,则这9个数的和为9a.
(3)成立.因为这9个数可以表示为,所以其和为9a.
(4)关系很多,例如:每一竖列上的数依次相差7,每一横行上的数依次相差1.
当堂达标
1.C 解析:首先根据上面的数值变化规律求出m的值为7,然后根据每个方格中的上面的数乘下面左侧的数再加上上面的数得下面右侧的数,求n即可.从方格上方的1,3,5,可以推出m=7;第一个方格中,3=1×2+1;第二个方格中,15=3×4+3;第三个方格中,35=5×6+5;所以第四个方格中,n=7×8+7=63.故选C.
2.C 解析:由题图知第①个图案需要黑色棋子的个数为(1+2+3)×2,第②个图案需要黑色棋子的个数为(1+2+3+4)×2+2×1,第③个图案需要黑色棋子的个数为(1+2+3+4+5)×2+2×2,第④个图案需要黑色棋子的个数为(1+2+3+4+5+6)×2+2×3,…,第个图案需要黑色棋子的个数为[1+2+3+…+(n+2)]×2+2(n-1),∴ 第⑩个图案需要黑色棋子的个数为(1+2+3+4+5+6+7+8+9+10+11+12)×2+2×9=174.故选C.
3.20 110 解析:由已知数据1,3,6,10,15,…,可得an=,
∴ a200==20 100,∴ a4+a200=10+20 100=20 110.
4.答案不唯一.如可填a+d=b+c.
解析:根据日历中的规律:b=a+1,c=a+7,d=a+8.
本题的答案不唯一,认真观察分析,还能得出一些其他的规律,如a+b+14=c+d,c-a=d-b等.
5.21 解析:∵ 第一位同学报,第二位同学报,第三位同学报,…,
∴ 这样得到的20个数分别为=2,=,=,…,=,=,故这样得到的20个数的积为2×=21,故答案为21.
课后提升
1.6 022 解析:根据题意,观察可得A,B两行每一行的数字变化规律及数字个数,类比可得C行的变化规律,进而可得最后的一个数字.观察可得:A行,第一个数为2,每一个比下一个小1,最后一个数为2 009,共2 008个数;B行,第一个数为1,每一个比下一个小1,最后一个数为2 008,共2 008个数;C行,第一个数为1,每一个比下一个小3,第n个数为3×n-2,则最后一个数为2 008×3-2=6 022.故表格中最右一栏中的x的值等于6 022.
2.解:设平行四边形正中间的数为a,则此9个数的和为9a.
①因为1 993不是9的倍数,所以不可能找到这样的平行四边形,使其中九个数的和等于1 993.
②1 143÷9=127,127÷8=15……7,这就是说如果1 143是符合条件的九个数的和,则正中间的数一定是127,而127位于数表中从右边数的第2列,但从题中的图容易看出:平行四边形正中间的数不能位于第1行,也不能位于从左数的第1列、第2列、第7列和第8列,因此不可能构成以127为中心的平行四边形.
③1 989÷9=221,221÷8=27……5,即1 989是9的倍数,九个数的和为1 989的平行四边形如图8,其中最大的数是229,最小的数是213.
图8
5 探索与表达规律
第2课时 表达规律
学习目标
1.会用代数式表达规律,能利用代数式的运算解释具体问题中蕴含的一般规律及现象.(重难点)
2.在解决问题的过程中体验归纳、分析、猜想、抽象、类比、转化等思维方法,发展抽象思维能力.(难点)
自主学习
学习任务 表达规律
做游戏
1.准备一副扑克牌,按下列步骤操作.请同学们按操作步骤完成表格.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张放入中间
第三步,从右边拿出1张放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
2.如果用a(a>2)表示左、中、右三堆牌开始的张数,请你按照操作步骤求出中间一堆牌最后的张数.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张放入中间
第三步,从右边拿出1张放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
合作探究
猜数游戏
游戏规则:你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5,最后将得到的数加原来两位数的个位数字.把你的结果告诉我,我就知道你心里想的两位数.
(1)如果心里想的两位数是12,则最后得到的数是多少?如果心里想的两位数是78,则最后得到的数是多少?
(2)从问题(1)你发现游戏结果与心里想的两位数有什么关系?
(3)请用字母表达并借助代数式的运算解释其中的道理.
当堂达标
1.甲、乙两同学进行数字猜谜游戏:甲说一个数a的相反数就是它本身,乙说一个数b的倒数也等于它本身,请你猜一猜|a-b|= .
2.猜数游戏
请你随便想一个数,并将此数乘5加7,然后再将结果乘2减4,你将最后结果告诉我,我心里将这个结果减10,再除以10,我就能知道你想的数.你能用字母表达并借助代数式的运算解释其中的道理吗?
3.田老师在数学课上带领同学们做数学游戏,规则如下:
游戏规则 甲任报一个有理数传给乙; 乙把这个数减2后报给丙; 丙再把所得的数的绝对值报给丁; 丁再把这个数的一半减1,报出答案.
根据游戏规则,回答下面的问题.
(1)若甲报的数为,则乙报的数为 ,丁报出的答案是 ;
(2)若甲报的数为-3,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是0,请写出甲报的数.
课后提升
猜年龄
当你变成你父亲的年龄时,父亲多少岁了?只要你用现在父亲的年龄的2倍减去那时父亲的年龄,把结果告诉我,我就能知道你现在的年龄.请你用字母表达并借助代数式的运算解释其中的道理.
反思感悟
我的收获:
我的易错点:
参考答案
自主学习
学习任务
1.解:
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张放入中间 3-2 3+2 3
第三步,从右边拿出1张放入中间 3-2 3+2+1 3-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 3-2+(3-2) 3+2+1-(3-2) 3-1
结果得出中间一堆牌现有的张数 3+2+1-(3-2)=5
2.解:
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张放入中间 a-2 a+2 a
第三步,从右边拿出1张放入中间 a-2 a+2+1 a-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 a-2+(a-2) a+2+1-(a-2) a-1
结果得出中间一堆牌现有的张数 a+2+1-(a-2)=5
合作探究
解:(1)27,93. (2)游戏结果比心里想的两位数大15.
(3)设心里想的两位数的十位数字为a,个位数字为b,则这个两位数可以表示为10a+b,则游戏结果为5(2a+3)+b=10a+15+b=(10a+b)+15.所以用计算结果减15,就得到心里想的两位数.
当堂达标
1.1 解析:相反数就是它本身的数是0;倒数等于它本身的数是1或-1.当a=0,b=1时,|a-b|=1;当a=0,b=-1时,|a-b|=1.总之|a-b|=1.
2.解:设心里想的数为a,根据游戏规则可得
{[(5a+7)×2-4]-10}÷10=(10a+14-4-10)÷10=10a÷10=a.
根据游戏规则最后得到的数与心里想的数相同.
3.(1) 解析:若甲报的数为,则乙报的数为-2=,
则丙报的数是,丁报出的答案为.
(2)解:若甲报的数为-3,则丁报出的答案为|-3-2|×-1.
因为|-3-2|×-1=5×-1=,所以丁报出的答案是.
(3)解:设甲报的数为x,由题意,得|x-2|×-1=0,所以|x-2|×=1,所以|x-2|=2,
所以x-2=2或x-2=-2,所以x=4或x=0.所以甲报的数是4或0.
课后提升
解:设你现在的年龄为a岁,父亲现在的年龄为b岁.父亲和你的年龄相差(b-a)岁.假如你变成父亲的年龄b岁,则父亲的年龄变成b+(b-a)=(2b-a)(岁).根据题意,得2b-(2b-a)=2b-2b+a=a(岁).所得结果恰好是你现在的年龄 .所以只要你把结果告诉我,我就能知道你现在的年龄.
第1课时 探索规律
学习目标
1.会用代数式表达规律,并能借助代数式的运算验证所探索的规律的一般性.(重难点)
2.经历探索数量关系、运用符号表达规律,体会探索规律的一般方法.(难点)
自主学习
学习任务 日历中的数字规律
观察教材第98页的日历图,回答下列问题.
1.(1)横行上相邻的两个数相差多少?
(2)如果用a表示横行上的第一个数,则与它相邻的右边的两个数分别表示为
与 .
2.(1)竖列上相邻的两个数相差多少?
(2)如果用a表示竖列上的最上面的数,则与它相邻的下面的两个数分别表示为
与 .
3.(1)斜列上从左上到右下相邻两数相差多少?从右上到左下相邻两数相差多少?
(2)如果用a表示左上的数,则与它相邻的右下的两个数分别表示为 与 ;如果用a表示右上的数,则与它相邻的左下的两个数分别表示为 与 .
4.如图1所示,如果用a表示日历图3×3方框(每个方框中都有数)中的中间数,请你填出方框中另外的8个数.
a
图1
合作探究
如图2所示,观察日历图,完成下列问题.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
图2
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?
(3)这个关系对任何一个月的日历都成立吗?为什么?
(4)你还能发现这样的方框中9个数之间的其他关系吗?
当堂达标
1.如图3所示,填在各方框中的三个数之间均具有相同的规律,根据此规律,n的值是( )
图3
A.48 B.56 C.63 D.74
2.(山东德州中考)图4是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )
② ③ ④
图4
A.148 B.152 C.174 D.202
3.(山东泰安中考)图5被称为“杨辉三角”或“贾宪三角”,其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.图中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,则a4+a200= .
图5
4.图6是某月的日历,现用一方框在日历中任意框出四个数,请用一个等式表示a,b,c,d之间的关系 (只要填一个即可).
日 一 二 三 四 五 六
1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30
图6
5.某数学活动小组的20名同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己的顺序数的倒数加1,第一位同学报,第二位同学报,第三位同学报,…,这样得到的20个数的积为 .
课后提升
1.某种数字游戏规律如下表所示:
A行 2 3 4 5 6 … 2 009
B行 1 2 3 4 5 … 2 008
C行 1 4 7 10 13 … x
按此规律,则表格中最右一栏中的x的值等于 .
2.从1开始的自然数按如图7所示的规则排列,并用一个平行四边形框出9个数,能否使这九个数的和等于①1 993;②1 143;③1 989?若能办到,请写出平行四边形框内的最大数和最小数;若不能办到,说明理由.
图7
反思感悟
我的收获:
我的易错点:
参考答案
自主学习
学习任务
1.(1)1 (2)a+1 a+2
2.(1)7 (2)a+7 a+14
3.(1)8 6 (2)a+8 a+16 a+6 a+12
4.解:
a-8 a-7 a-6
a-1 a a+1
a+6 a+7 a+8
合作探究
解:(1)9个数之和为90,90=10×9,这9个数之和是中间数的9倍.
(2)成立.设中间数为a,则这9个数的和为9a.
(3)成立.因为这9个数可以表示为,所以其和为9a.
(4)关系很多,例如:每一竖列上的数依次相差7,每一横行上的数依次相差1.
当堂达标
1.C 解析:首先根据上面的数值变化规律求出m的值为7,然后根据每个方格中的上面的数乘下面左侧的数再加上上面的数得下面右侧的数,求n即可.从方格上方的1,3,5,可以推出m=7;第一个方格中,3=1×2+1;第二个方格中,15=3×4+3;第三个方格中,35=5×6+5;所以第四个方格中,n=7×8+7=63.故选C.
2.C 解析:由题图知第①个图案需要黑色棋子的个数为(1+2+3)×2,第②个图案需要黑色棋子的个数为(1+2+3+4)×2+2×1,第③个图案需要黑色棋子的个数为(1+2+3+4+5)×2+2×2,第④个图案需要黑色棋子的个数为(1+2+3+4+5+6)×2+2×3,…,第个图案需要黑色棋子的个数为[1+2+3+…+(n+2)]×2+2(n-1),∴ 第⑩个图案需要黑色棋子的个数为(1+2+3+4+5+6+7+8+9+10+11+12)×2+2×9=174.故选C.
3.20 110 解析:由已知数据1,3,6,10,15,…,可得an=,
∴ a200==20 100,∴ a4+a200=10+20 100=20 110.
4.答案不唯一.如可填a+d=b+c.
解析:根据日历中的规律:b=a+1,c=a+7,d=a+8.
本题的答案不唯一,认真观察分析,还能得出一些其他的规律,如a+b+14=c+d,c-a=d-b等.
5.21 解析:∵ 第一位同学报,第二位同学报,第三位同学报,…,
∴ 这样得到的20个数分别为=2,=,=,…,=,=,故这样得到的20个数的积为2×=21,故答案为21.
课后提升
1.6 022 解析:根据题意,观察可得A,B两行每一行的数字变化规律及数字个数,类比可得C行的变化规律,进而可得最后的一个数字.观察可得:A行,第一个数为2,每一个比下一个小1,最后一个数为2 009,共2 008个数;B行,第一个数为1,每一个比下一个小1,最后一个数为2 008,共2 008个数;C行,第一个数为1,每一个比下一个小3,第n个数为3×n-2,则最后一个数为2 008×3-2=6 022.故表格中最右一栏中的x的值等于6 022.
2.解:设平行四边形正中间的数为a,则此9个数的和为9a.
①因为1 993不是9的倍数,所以不可能找到这样的平行四边形,使其中九个数的和等于1 993.
②1 143÷9=127,127÷8=15……7,这就是说如果1 143是符合条件的九个数的和,则正中间的数一定是127,而127位于数表中从右边数的第2列,但从题中的图容易看出:平行四边形正中间的数不能位于第1行,也不能位于从左数的第1列、第2列、第7列和第8列,因此不可能构成以127为中心的平行四边形.
③1 989÷9=221,221÷8=27……5,即1 989是9的倍数,九个数的和为1 989的平行四边形如图8,其中最大的数是229,最小的数是213.
图8
5 探索与表达规律
第2课时 表达规律
学习目标
1.会用代数式表达规律,能利用代数式的运算解释具体问题中蕴含的一般规律及现象.(重难点)
2.在解决问题的过程中体验归纳、分析、猜想、抽象、类比、转化等思维方法,发展抽象思维能力.(难点)
自主学习
学习任务 表达规律
做游戏
1.准备一副扑克牌,按下列步骤操作.请同学们按操作步骤完成表格.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张放入中间
第三步,从右边拿出1张放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
2.如果用a(a>2)表示左、中、右三堆牌开始的张数,请你按照操作步骤求出中间一堆牌最后的张数.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张放入中间
第三步,从右边拿出1张放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
合作探究
猜数游戏
游戏规则:你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5,最后将得到的数加原来两位数的个位数字.把你的结果告诉我,我就知道你心里想的两位数.
(1)如果心里想的两位数是12,则最后得到的数是多少?如果心里想的两位数是78,则最后得到的数是多少?
(2)从问题(1)你发现游戏结果与心里想的两位数有什么关系?
(3)请用字母表达并借助代数式的运算解释其中的道理.
当堂达标
1.甲、乙两同学进行数字猜谜游戏:甲说一个数a的相反数就是它本身,乙说一个数b的倒数也等于它本身,请你猜一猜|a-b|= .
2.猜数游戏
请你随便想一个数,并将此数乘5加7,然后再将结果乘2减4,你将最后结果告诉我,我心里将这个结果减10,再除以10,我就能知道你想的数.你能用字母表达并借助代数式的运算解释其中的道理吗?
3.田老师在数学课上带领同学们做数学游戏,规则如下:
游戏规则 甲任报一个有理数传给乙; 乙把这个数减2后报给丙; 丙再把所得的数的绝对值报给丁; 丁再把这个数的一半减1,报出答案.
根据游戏规则,回答下面的问题.
(1)若甲报的数为,则乙报的数为 ,丁报出的答案是 ;
(2)若甲报的数为-3,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是0,请写出甲报的数.
课后提升
猜年龄
当你变成你父亲的年龄时,父亲多少岁了?只要你用现在父亲的年龄的2倍减去那时父亲的年龄,把结果告诉我,我就能知道你现在的年龄.请你用字母表达并借助代数式的运算解释其中的道理.
反思感悟
我的收获:
我的易错点:
参考答案
自主学习
学习任务
1.解:
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张放入中间 3-2 3+2 3
第三步,从右边拿出1张放入中间 3-2 3+2+1 3-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 3-2+(3-2) 3+2+1-(3-2) 3-1
结果得出中间一堆牌现有的张数 3+2+1-(3-2)=5
2.解:
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张放入中间 a-2 a+2 a
第三步,从右边拿出1张放入中间 a-2 a+2+1 a-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 a-2+(a-2) a+2+1-(a-2) a-1
结果得出中间一堆牌现有的张数 a+2+1-(a-2)=5
合作探究
解:(1)27,93. (2)游戏结果比心里想的两位数大15.
(3)设心里想的两位数的十位数字为a,个位数字为b,则这个两位数可以表示为10a+b,则游戏结果为5(2a+3)+b=10a+15+b=(10a+b)+15.所以用计算结果减15,就得到心里想的两位数.
当堂达标
1.1 解析:相反数就是它本身的数是0;倒数等于它本身的数是1或-1.当a=0,b=1时,|a-b|=1;当a=0,b=-1时,|a-b|=1.总之|a-b|=1.
2.解:设心里想的数为a,根据游戏规则可得
{[(5a+7)×2-4]-10}÷10=(10a+14-4-10)÷10=10a÷10=a.
根据游戏规则最后得到的数与心里想的数相同.
3.(1) 解析:若甲报的数为,则乙报的数为-2=,
则丙报的数是,丁报出的答案为.
(2)解:若甲报的数为-3,则丁报出的答案为|-3-2|×-1.
因为|-3-2|×-1=5×-1=,所以丁报出的答案是.
(3)解:设甲报的数为x,由题意,得|x-2|×-1=0,所以|x-2|×=1,所以|x-2|=2,
所以x-2=2或x-2=-2,所以x=4或x=0.所以甲报的数是4或0.
课后提升
解:设你现在的年龄为a岁,父亲现在的年龄为b岁.父亲和你的年龄相差(b-a)岁.假如你变成父亲的年龄b岁,则父亲的年龄变成b+(b-a)=(2b-a)(岁).根据题意,得2b-(2b-a)=2b-2b+a=a(岁).所得结果恰好是你现在的年龄 .所以只要你把结果告诉我,我就能知道你现在的年龄.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
