人教版数学九年级上册 24.3 正多边形和圆(2) 教案
文档属性
| 名称 | 人教版数学九年级上册 24.3 正多边形和圆(2) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 314.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 14:39:27 | ||
图片预览

文档简介
24.3 正多边形和圆
第2课时
一、教学目标
【知识与技能】
会用圆规、量角器和直尺来作圆内接正多边形.
【过程与方法】
用圆的有关知识,解决正多边形的问题.
【情感态度与价值观】
学生经历观察、发现、探究等数学活动,感受到事物之间是相互联系,相互作用的.
二、课型
新授课
三、课时
第2课时,共2课时。
四、教学重难点
【教学重点】
作圆内接正多边形.
【教学难点】
作圆内接正多边形.
五、课前准备
课件、图片、圆规、量角器、直尺等.
六、教学过程
(一)导入新课
正多边形和圆有什么关系?你能借助圆画一个正多边形吗?(出示课件2)
(二)探索新知
探究 正多边形的画法
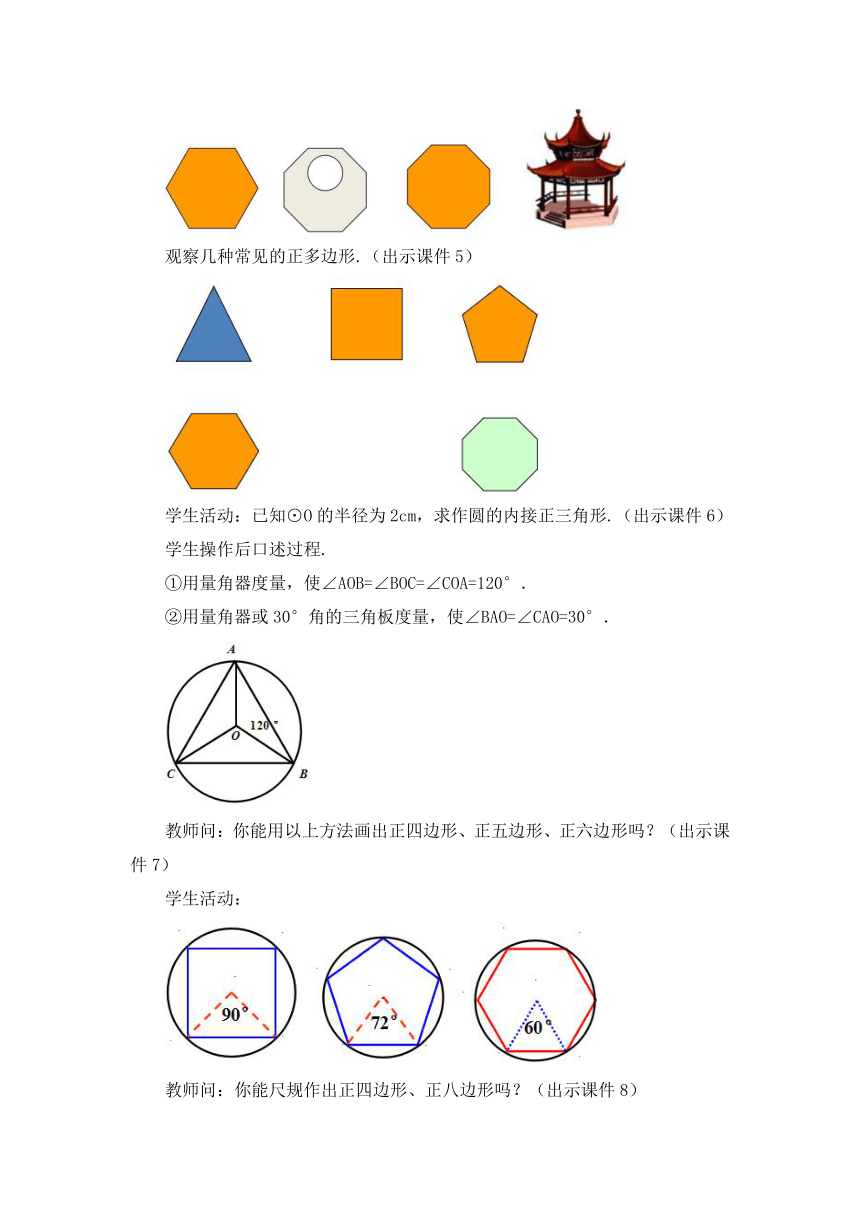
学生活动:观察生活中的正多边形图案.(出示课件4)
观察几种常见的正多边形.(出示课件5)
学生活动:已知⊙O的半径为2cm,求作圆的内接正三角形.(出示课件6)
学生操作后口述过程.
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
教师问:你能用以上方法画出正四边形、正五边形、正六边形吗?(出示课件7)
学生活动:
教师问:你能尺规作出正四边形、正八边形吗?(出示课件8)
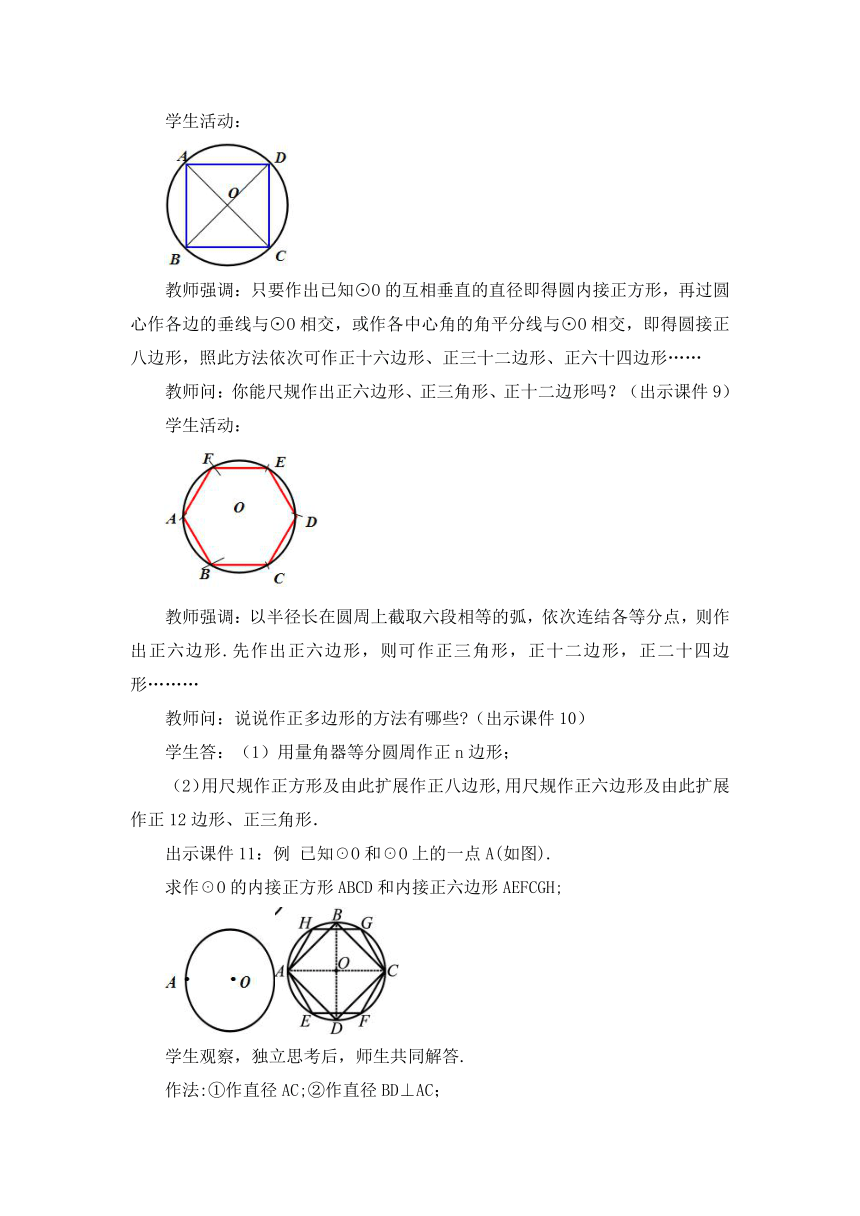
学生活动:
教师强调:只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
教师问:你能尺规作出正六边形、正三角形、正十二边形吗?(出示课件9)
学生活动:
教师强调:以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
教师问:说说作正多边形的方法有哪些 (出示课件10)
学生答:(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形,用尺规作正六边形及由此扩展作正12边形、正三角形.
出示课件11:例 已知☉O和☉O上的一点A(如图).
求作☉O的内接正方形ABCD和内接正六边形AEFCGH;
学生观察,独立思考后,师生共同解答.
作法:①作直径AC;②作直径BD⊥AC;
③依次连接A、B、C、D四点,
∴四边形ABCD即为☉O的内接正方形;
④分别以A、C为圆心,OA的长为半径作弧,
交☉O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点;
∴六边形AEFCGH为☉O的内接正六边形,如图所示.
巩固练习:(出示课件12)
画一个半径为2cm的正五边形,再作出这个正五边形的各条对角线,画出一个五角星.
学生自主操作.
(三)课堂练习(出示课件13-18)
1.尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A、B、C、D、E、F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?
大臣给出的正确答案应是( )
A.r B.(1+)r C.(1+)r D.r
2.在图中,用尺规作图画出圆O的内接正三角形.
3.利用量角器画一个边长为2cm的正六边形.
4.一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周率”,下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a1,a2,a3,a4,则下列关系中正确的是( )
A.a4>a2>a1 B.a4>a3>a2 C.a1>a2>a3 D.a2>a3>a4
5.画一个正十二边形.
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
7.如图,正六边形ABCDEF的边长为,点P为六边形内任一点.则点P到各边距离之和是多少?
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;
(2)试探究∠MON的度数与正n边形的边数n的关系.
参考答案:
1.D
2.作法:
⑴作出圆的任意一条半径,
⑵作半径的垂直平分线,交圆于点A、B,
⑶分别以A、B为圆心,线段AB的长为半径作弧,两户交于点C,连接AC、BC.则△ABC即为所求.
3.作法:如图,以2cm为半径作一个⊙O,用量角器画一个等于的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
4.B
5.作法:如图,分别以⊙O的四等分点A,B,E,F为圆心,以⊙O的半径长为半径,画8条弧与⊙O相交,就可以把⊙O分成12等份,依次连接各等分点,即得到正十二边形.
(四)课堂小结
通过这节课的学习,你知道正多边形和圆有怎样的关系吗?
(五)课前预习
预习下节课(24.4第1课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
1.画正多边形的方法:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角就可以等分圆周,从而得到相应的正多边形.
2.画正多边形的方法:
⑴用量角器等分圆;
⑵尺规作图等分圆.
九、教学反思:
等分圆周法是一种作正多边形的常见方法,通过作简单的正三角形、正方形、正六边形,一直推广到作正八边形的情况,可以向学生灌输极限的思想,极限是微积分中最主要、最基本的概念,它从数量上描述变量在变化过程中的变化趋势,在高中数学中,极限思想渗透到函数、数列等章节,又衔接高等数学,起着承上启下的作用.
第2课时
一、教学目标
【知识与技能】
会用圆规、量角器和直尺来作圆内接正多边形.
【过程与方法】
用圆的有关知识,解决正多边形的问题.
【情感态度与价值观】
学生经历观察、发现、探究等数学活动,感受到事物之间是相互联系,相互作用的.
二、课型
新授课
三、课时
第2课时,共2课时。
四、教学重难点
【教学重点】
作圆内接正多边形.
【教学难点】
作圆内接正多边形.
五、课前准备
课件、图片、圆规、量角器、直尺等.
六、教学过程
(一)导入新课
正多边形和圆有什么关系?你能借助圆画一个正多边形吗?(出示课件2)
(二)探索新知
探究 正多边形的画法
学生活动:观察生活中的正多边形图案.(出示课件4)
观察几种常见的正多边形.(出示课件5)
学生活动:已知⊙O的半径为2cm,求作圆的内接正三角形.(出示课件6)
学生操作后口述过程.
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
教师问:你能用以上方法画出正四边形、正五边形、正六边形吗?(出示课件7)
学生活动:
教师问:你能尺规作出正四边形、正八边形吗?(出示课件8)
学生活动:
教师强调:只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
教师问:你能尺规作出正六边形、正三角形、正十二边形吗?(出示课件9)
学生活动:
教师强调:以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
教师问:说说作正多边形的方法有哪些 (出示课件10)
学生答:(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形,用尺规作正六边形及由此扩展作正12边形、正三角形.
出示课件11:例 已知☉O和☉O上的一点A(如图).
求作☉O的内接正方形ABCD和内接正六边形AEFCGH;
学生观察,独立思考后,师生共同解答.
作法:①作直径AC;②作直径BD⊥AC;
③依次连接A、B、C、D四点,
∴四边形ABCD即为☉O的内接正方形;
④分别以A、C为圆心,OA的长为半径作弧,
交☉O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点;
∴六边形AEFCGH为☉O的内接正六边形,如图所示.
巩固练习:(出示课件12)
画一个半径为2cm的正五边形,再作出这个正五边形的各条对角线,画出一个五角星.
学生自主操作.
(三)课堂练习(出示课件13-18)
1.尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A、B、C、D、E、F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?
大臣给出的正确答案应是( )
A.r B.(1+)r C.(1+)r D.r
2.在图中,用尺规作图画出圆O的内接正三角形.
3.利用量角器画一个边长为2cm的正六边形.
4.一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周率”,下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a1,a2,a3,a4,则下列关系中正确的是( )
A.a4>a2>a1 B.a4>a3>a2 C.a1>a2>a3 D.a2>a3>a4
5.画一个正十二边形.
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
7.如图,正六边形ABCDEF的边长为,点P为六边形内任一点.则点P到各边距离之和是多少?
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;
(2)试探究∠MON的度数与正n边形的边数n的关系.
参考答案:
1.D
2.作法:
⑴作出圆的任意一条半径,
⑵作半径的垂直平分线,交圆于点A、B,
⑶分别以A、B为圆心,线段AB的长为半径作弧,两户交于点C,连接AC、BC.则△ABC即为所求.
3.作法:如图,以2cm为半径作一个⊙O,用量角器画一个等于的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
4.B
5.作法:如图,分别以⊙O的四等分点A,B,E,F为圆心,以⊙O的半径长为半径,画8条弧与⊙O相交,就可以把⊙O分成12等份,依次连接各等分点,即得到正十二边形.
(四)课堂小结
通过这节课的学习,你知道正多边形和圆有怎样的关系吗?
(五)课前预习
预习下节课(24.4第1课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
1.画正多边形的方法:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角就可以等分圆周,从而得到相应的正多边形.
2.画正多边形的方法:
⑴用量角器等分圆;
⑵尺规作图等分圆.
九、教学反思:
等分圆周法是一种作正多边形的常见方法,通过作简单的正三角形、正方形、正六边形,一直推广到作正八边形的情况,可以向学生灌输极限的思想,极限是微积分中最主要、最基本的概念,它从数量上描述变量在变化过程中的变化趋势,在高中数学中,极限思想渗透到函数、数列等章节,又衔接高等数学,起着承上启下的作用.
同课章节目录
