人教版六年级上册数学第八单元数学广角--数与形解答题专题训练(含答案)
文档属性
| 名称 | 人教版六年级上册数学第八单元数学广角--数与形解答题专题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览


文档简介
人教版六年级上册数学第八单元 数学广角--数与形解答题专题训练
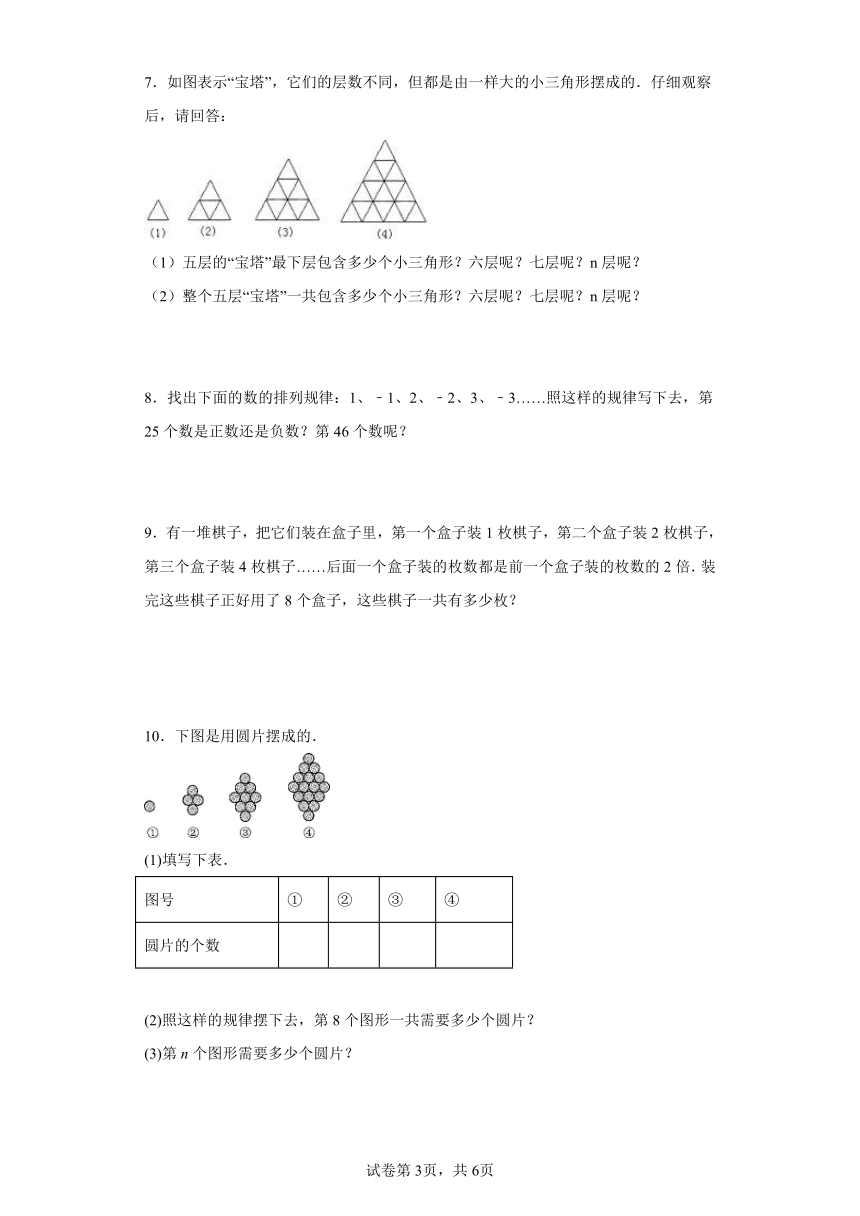
1.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,…照这样计算,10张桌子并成一排可坐多少人?如果一共有26人,需要并多少张桌子?
2.
图形 … … … …
三角形个数 1 2 3 4 … 10 n
所需火柴数 3 5 7 9 … 1001
(1)10个三角形需要几根火柴?摆n个呢?
(2)如果有1001根火柴可以摆几个三角形?
3.刘老师把自然数(0除外)按下面的样子排列.
(1)照下面的规律排下去,第6行有多少个数?第10行有多少个数?
(2)第1行到第6行一共有多少个数?
(3)第1行到第5行所有数相加的和是多少?
4.小明把巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒.请问:
(1)一共有多少个巧克力棒?
(2)这些巧克力棒共构成了多少个三角形?
(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?
5.用小棒按照如下方式摆图形.
(1)摆1个八边形需要8根小棒,摆2个八边形需要( )根小棒,摆3个八边形需要( )根小棒,摆20个八边形需要( )根小棒。
(2)如果想摆a个八边形,需要( )根小棒。
(3)有2010根小棒,可以摆( )个这样的八边形。
6.我会发现规律.
三角形的个数 1 2 3 4 5 6 ……
小棒的根数 3 5 ……
1.摆20个这样的三角形,需要多少根小棒?
2.有99根小棒,能摆出多少个这样的三角形?
7.如图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:
(1)五层的“宝塔”最下层包含多少个小三角形?六层呢?七层呢?n层呢?
(2)整个五层“宝塔”一共包含多少个小三角形?六层呢?七层呢?n层呢?
8.找出下面的数的排列规律:1、﹣1、2、﹣2、3、﹣3……照这样的规律写下去,第25个数是正数还是负数?第46个数呢?
9.有一堆棋子,把它们装在盒子里,第一个盒子装1枚棋子,第二个盒子装2枚棋子,第三个盒子装4枚棋子……后面一个盒子装的枚数都是前一个盒子装的枚数的2倍.装完这些棋子正好用了8个盒子,这些棋子一共有多少枚?
10.下图是用圆片摆成的.
(1)填写下表.
图号 ① ② ③ ④
圆片的个数
(2)照这样的规律摆下去,第8个图形一共需要多少个圆片?
(3)第n个图形需要多少个圆片?
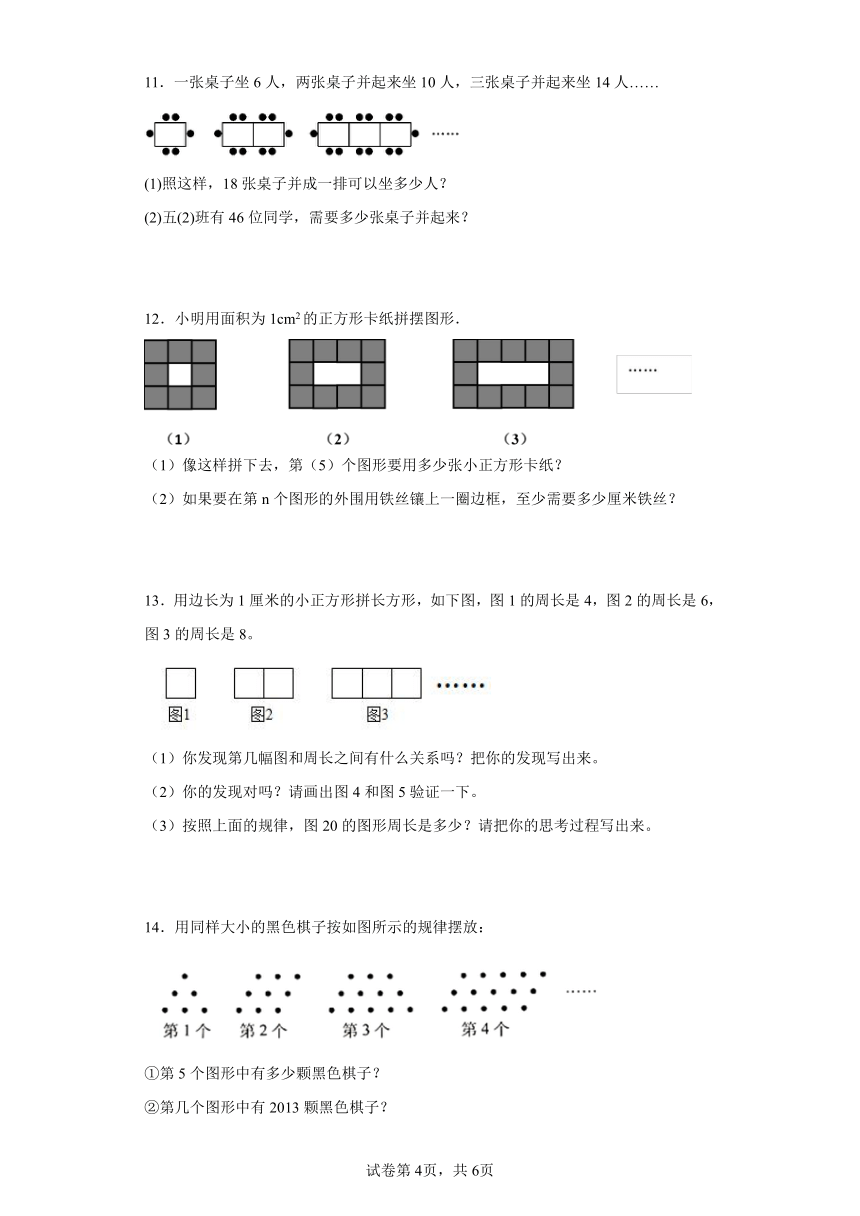
11.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……
(1)照这样,18张桌子并成一排可以坐多少人?
(2)五(2)班有46位同学,需要多少张桌子并起来?
12.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
13.用边长为1厘米的小正方形拼长方形,如下图,图1的周长是4,图2的周长是6,图3的周长是8。
(1)你发现第几幅图和周长之间有什么关系吗?把你的发现写出来。
(2)你的发现对吗?请画出图4和图5验证一下。
(3)按照上面的规律,图20的图形周长是多少?请把你的思考过程写出来。
14.用同样大小的黑色棋子按如图所示的规律摆放:
①第5个图形中有多少颗黑色棋子?
②第几个图形中有2013颗黑色棋子?
15.下列图案由边长相等的黑、白两色小正方形按一定规律拼接而成.
黑色:1 2 3
白色:8 13 18
照这样画下去,第10个图形中分别有多少个黑色小正方形和白色小正方形?你能解释其中的道理吗?
16.摆一个六边形要用6根小棒,连摆两个六边形要用11根小棒,连摆三个六边形要用16根小棒……照这样摆下去.
(1)连续摆n个三角形,要用多少根小棒?
(2)当n=100时,需要多少根小棒?
(3)如果有101根小棒,可以连摆多少个这样的六边形?
17.
(1)用同样大小的黑色棋子按上图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需要黑色棋子( )枚。(用含n的代数式表示)
(2)用第(1)题中的式子计算第22个图形中有多少枚黑色棋子。
18.下面都是由边长为1厘米的小正方形拼成的大正方形。
……
(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2
周围正方形个数(个) 8 12
(2)以此类推,你知道图⑨中涂色部分的周围共有多少个小正方形吗?
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.解:(I)n=1时,可坐4人,可以写成2×1+2
n=2时,可坐6人,可以写成2×2+2
n=3时,可坐8人,可以写成2×3=2
…
所以当n=10时,可坐2×10+2=22人
答:10张桌子并成一排可坐22人.
(II)2n+2=26
2n=24
n=12
答:如果有26人,需要12张桌子.
2.(1)解:当三角形的个数为1时,火柴棒的根数为3=1+1×2;
当三角形的个数为2时,火柴棒的根数为5=1+2×2;
当三角形的个数为3时,火柴棒的根数为7=1+3×2;…
由此可以看出:当三角形的个数为n时,火柴棒的根数为1+2n.
当n=10时,需要小棒:1+2×10=21(根),
答:10个三角形需要21根小棒,摆成n个三角形,需要小棒1+2n根.
(2)解:当小棒有1001根时,代入上述关系式可得:1+2n=1001,则n=500,即可以摆成50个小三角形;
答:1001根小棒可以摆成500个小三角形.
由此计算即可完成上表如下所示:
图形 … … … …
三角形个数 1 2 3 4 … 10 500 n
所需火柴数 3 5 7 9 … 21 1001 1+2n
3.(1)第6行有:6×2-1=11(个)
第10行有:10×2-1=19(个)
(2)1+3+5+7+9+11=36(个)
(3)1+2+3+…+25=325 点拨:因为第5行有5×2-1=9(个)数,所以从第1行到第5行一共有1+3+5+7+9=25(个)数,这25个数就是1~25,再求和.
4.(1)30个(2)27个(3)22个
5. (1)15 22 141 (2)7a+1 (3)287
6.7 9 11 13 1.结合图形,发现:搭第n个图形,需要3+2(n-1)=2n+1(根) 当n=20时,需要小棒:20×2+1=41(根)
答:摆20个这样的三角形,需要41根小棒. 2.当2n+1=99时,n=49 答:99根小棒能摆出49个这样的三角形.
7.(1)五层的“宝塔”最下层包含9个小三角形,六层有11个,七层有13个,n层有2n-1个.
(2)整个五层“宝塔”一共包含25个小三角形,六层有36个,七层有49个,n层有n2个.
8.第25个数是正数,第46个数是负数。
9.255枚
10.(1)1 4 9 16
(2)8×8=64(个)
(3)第n个图形需要n2个圆片.
11.(1) 74人
(2) 11张
12.(1)16张;(2)(10+2n)厘米.
13.(1)第几幅图加1的和再乘2是它的周长。
(2)对;
(3)42厘米
14.①18颗
②第670个图形
15.黑色10个,白色53个;道理:每增加一个黑色小正方形,就增加5个白色小正方形.
16.(1)(5n+1)根 (2)501根 (3)20个
17.(1)3n+1
(2)67枚
18.(1)3;4;5
16;20;24
(2)40个
答案第2页,共3页
答案第3页,共3页
1.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,…照这样计算,10张桌子并成一排可坐多少人?如果一共有26人,需要并多少张桌子?
2.
图形 … … … …
三角形个数 1 2 3 4 … 10 n
所需火柴数 3 5 7 9 … 1001
(1)10个三角形需要几根火柴?摆n个呢?
(2)如果有1001根火柴可以摆几个三角形?
3.刘老师把自然数(0除外)按下面的样子排列.
(1)照下面的规律排下去,第6行有多少个数?第10行有多少个数?
(2)第1行到第6行一共有多少个数?
(3)第1行到第5行所有数相加的和是多少?
4.小明把巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒.请问:
(1)一共有多少个巧克力棒?
(2)这些巧克力棒共构成了多少个三角形?
(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?
5.用小棒按照如下方式摆图形.
(1)摆1个八边形需要8根小棒,摆2个八边形需要( )根小棒,摆3个八边形需要( )根小棒,摆20个八边形需要( )根小棒。
(2)如果想摆a个八边形,需要( )根小棒。
(3)有2010根小棒,可以摆( )个这样的八边形。
6.我会发现规律.
三角形的个数 1 2 3 4 5 6 ……
小棒的根数 3 5 ……
1.摆20个这样的三角形,需要多少根小棒?
2.有99根小棒,能摆出多少个这样的三角形?
7.如图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:
(1)五层的“宝塔”最下层包含多少个小三角形?六层呢?七层呢?n层呢?
(2)整个五层“宝塔”一共包含多少个小三角形?六层呢?七层呢?n层呢?
8.找出下面的数的排列规律:1、﹣1、2、﹣2、3、﹣3……照这样的规律写下去,第25个数是正数还是负数?第46个数呢?
9.有一堆棋子,把它们装在盒子里,第一个盒子装1枚棋子,第二个盒子装2枚棋子,第三个盒子装4枚棋子……后面一个盒子装的枚数都是前一个盒子装的枚数的2倍.装完这些棋子正好用了8个盒子,这些棋子一共有多少枚?
10.下图是用圆片摆成的.
(1)填写下表.
图号 ① ② ③ ④
圆片的个数
(2)照这样的规律摆下去,第8个图形一共需要多少个圆片?
(3)第n个图形需要多少个圆片?
11.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……
(1)照这样,18张桌子并成一排可以坐多少人?
(2)五(2)班有46位同学,需要多少张桌子并起来?
12.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
13.用边长为1厘米的小正方形拼长方形,如下图,图1的周长是4,图2的周长是6,图3的周长是8。
(1)你发现第几幅图和周长之间有什么关系吗?把你的发现写出来。
(2)你的发现对吗?请画出图4和图5验证一下。
(3)按照上面的规律,图20的图形周长是多少?请把你的思考过程写出来。
14.用同样大小的黑色棋子按如图所示的规律摆放:
①第5个图形中有多少颗黑色棋子?
②第几个图形中有2013颗黑色棋子?
15.下列图案由边长相等的黑、白两色小正方形按一定规律拼接而成.
黑色:1 2 3
白色:8 13 18
照这样画下去,第10个图形中分别有多少个黑色小正方形和白色小正方形?你能解释其中的道理吗?
16.摆一个六边形要用6根小棒,连摆两个六边形要用11根小棒,连摆三个六边形要用16根小棒……照这样摆下去.
(1)连续摆n个三角形,要用多少根小棒?
(2)当n=100时,需要多少根小棒?
(3)如果有101根小棒,可以连摆多少个这样的六边形?
17.
(1)用同样大小的黑色棋子按上图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需要黑色棋子( )枚。(用含n的代数式表示)
(2)用第(1)题中的式子计算第22个图形中有多少枚黑色棋子。
18.下面都是由边长为1厘米的小正方形拼成的大正方形。
……
(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2
周围正方形个数(个) 8 12
(2)以此类推,你知道图⑨中涂色部分的周围共有多少个小正方形吗?
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.解:(I)n=1时,可坐4人,可以写成2×1+2
n=2时,可坐6人,可以写成2×2+2
n=3时,可坐8人,可以写成2×3=2
…
所以当n=10时,可坐2×10+2=22人
答:10张桌子并成一排可坐22人.
(II)2n+2=26
2n=24
n=12
答:如果有26人,需要12张桌子.
2.(1)解:当三角形的个数为1时,火柴棒的根数为3=1+1×2;
当三角形的个数为2时,火柴棒的根数为5=1+2×2;
当三角形的个数为3时,火柴棒的根数为7=1+3×2;…
由此可以看出:当三角形的个数为n时,火柴棒的根数为1+2n.
当n=10时,需要小棒:1+2×10=21(根),
答:10个三角形需要21根小棒,摆成n个三角形,需要小棒1+2n根.
(2)解:当小棒有1001根时,代入上述关系式可得:1+2n=1001,则n=500,即可以摆成50个小三角形;
答:1001根小棒可以摆成500个小三角形.
由此计算即可完成上表如下所示:
图形 … … … …
三角形个数 1 2 3 4 … 10 500 n
所需火柴数 3 5 7 9 … 21 1001 1+2n
3.(1)第6行有:6×2-1=11(个)
第10行有:10×2-1=19(个)
(2)1+3+5+7+9+11=36(个)
(3)1+2+3+…+25=325 点拨:因为第5行有5×2-1=9(个)数,所以从第1行到第5行一共有1+3+5+7+9=25(个)数,这25个数就是1~25,再求和.
4.(1)30个(2)27个(3)22个
5. (1)15 22 141 (2)7a+1 (3)287
6.7 9 11 13 1.结合图形,发现:搭第n个图形,需要3+2(n-1)=2n+1(根) 当n=20时,需要小棒:20×2+1=41(根)
答:摆20个这样的三角形,需要41根小棒. 2.当2n+1=99时,n=49 答:99根小棒能摆出49个这样的三角形.
7.(1)五层的“宝塔”最下层包含9个小三角形,六层有11个,七层有13个,n层有2n-1个.
(2)整个五层“宝塔”一共包含25个小三角形,六层有36个,七层有49个,n层有n2个.
8.第25个数是正数,第46个数是负数。
9.255枚
10.(1)1 4 9 16
(2)8×8=64(个)
(3)第n个图形需要n2个圆片.
11.(1) 74人
(2) 11张
12.(1)16张;(2)(10+2n)厘米.
13.(1)第几幅图加1的和再乘2是它的周长。
(2)对;
(3)42厘米
14.①18颗
②第670个图形
15.黑色10个,白色53个;道理:每增加一个黑色小正方形,就增加5个白色小正方形.
16.(1)(5n+1)根 (2)501根 (3)20个
17.(1)3n+1
(2)67枚
18.(1)3;4;5
16;20;24
(2)40个
答案第2页,共3页
答案第3页,共3页
